Dla 10 losowo wybranych rodzin 4-osobowych miasta Z mamy następujące dane o dziennym zużyciu energii elektrycznej (w KWh): 13, 22, 15, 13, 20, 12, 14, 16, 18, 17. Czy liczebność tej próby jest wystarczająca, aby oszacować średnią zużycia dziennego energii elektrycznej dla populacji rodzin 4-osobowych miasta Z, jeżeli długość zbudowanego 90% przedziału ufności ma być mniejsza niż 3,8 KWh?

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Czy liczebność tej próby jest wystarczająca, aby oszacować średnią zużycia dziennego energii elektrycznej dla populacji rodzin 4-osobowych miasta Z, jeżeli długość zbudowanego 90% przedziału ufności ma być mniejsza niż 3,8 KWh? ”

Na początku może się wydawać, że zadanie dotyczy estymacji przedziałowej, ponieważ pojawia się zwrot: długość zbudowanego 90% przedziału ufności ... . Niemniej jednak przewagę nad tym wyrażeniem zawsze ma: czy liczebność próby jest wystarczająca .... , czyli szukamy minimalnej liczebności próby. Nie ma również ani słowa o maksymalnym błędzie szacunku, ale jest on ukryty w zadaniu pod innym szyldem. Nie jest to nic nadzwyczajnego, ponieważ zagadnienie minimalnej liczebności próby ściśle wiąże się z estymacją przedziałową. Biorąc to pod uwagę mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Dla 10 losowo wybranych rodzin 4-osobowych miasta Z mamy następujące dane o dziennym zużyciu energii elektrycznej (w KWh): 13, 22, 15, 13, 20, 12, 14, 16, 18, 17.

Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej tzw. pilotażowej, którą oznaczamy . Podano również informacje o konkretnych wynikach z próby. Jeżeli dysponujemy wartościami wypisanymi po przecinku tzw. 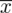danymi indywidualnymi, to zawsze możemy policzyć średnią , wariancję i odchylenie standardowe (lub , ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.

“ Czy liczebność tej próby jest wystarczająca, aby oszacować średnią zużycia dziennego energii elektrycznej dla populacji rodzin 4-osobowych miasta Z, jeżeli długość zbudowanego 90% przedziału ufności ma być mniejsza niż 3,8 KWh? ”

Szukamy liczebności próby (liczba rodzin), którą oznaczamy literą 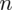. Podano również poziom ufności, a więc 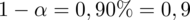. Od razu wyznaczamy 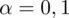. Jak pamiętamy, w zadaniach dotyczących minimalnej liczebności próby ważnym elementem jest wartość maksymalnego błędu szacunku 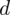. Zamiast tego dowiadujemy się, że przedział ufności powinien mieć długość nieprzekraczającą 3,8 KWh. Warto zapamiętać, że maksymalny błąd szacunku to połowa przedziału ufności. Jeśli informacja ta wydaje się być zbyt lakoniczna, odsyłam do szerszego wytłumaczenia http://matma-po-ludzku.pl/statystyka/wnioskowanie/estymacja/estymacja_sredniej/zadanie29.php . Otrzymujemy zatem .

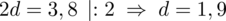Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA 4-osobowe rodziny miasta Z	PRÓBA 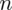wybranych rodzin
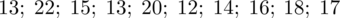	-dane indywidualne (można obliczyć średnią , wariancję 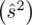, odchylenie standardowe )

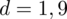
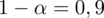- współczynnik ufności,

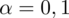
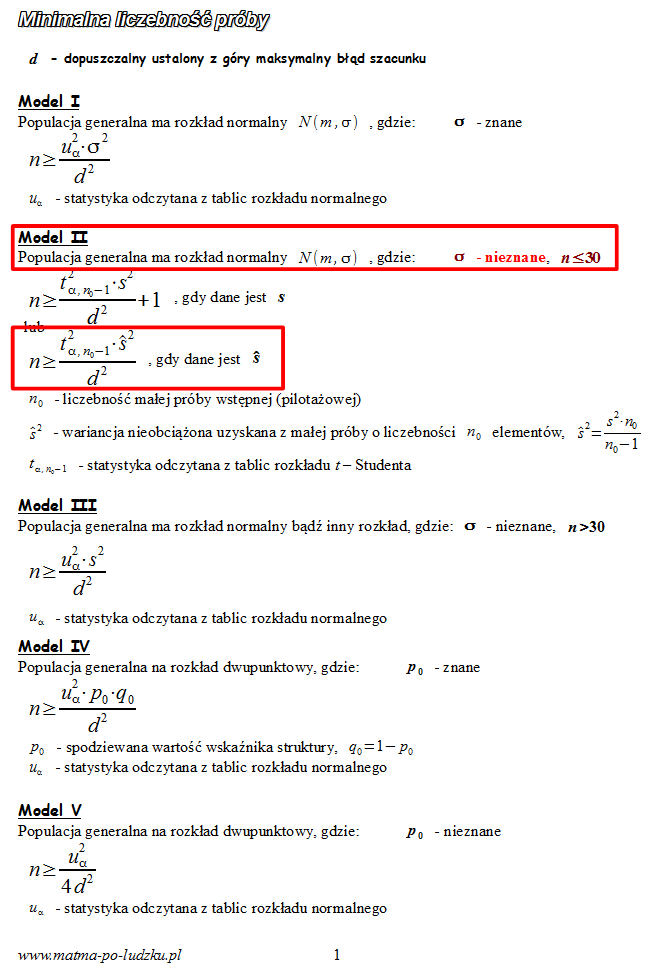
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ). Dysponując danymi indywidualnymi jesteśmy w stanie wyliczyć lub - wobec tego wybieramy model II . Którą wersję wzoru wybierzemy, zależy od nas. Znacznie częściej używana jest wersja z (z daszkiem), więc i ja wybiorę tą wersję.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 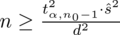konkretnymi liczbami.

Jak widać brakuje tylko , więc dopóki nie znajdziemy wartości tego parametru nie możemy obliczyć liczebności próby właściwej. Wyliczanie wariancji z próby jest zagadnieniem ze statystki opisowej.

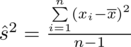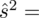
Dysponujemy danymi indywidualnymi (wynikami wypisanymi po przecinku), jest ich niewiele i nie powtarzają się w dużych ilościach, zatem wariancję liczymy ze wzoru związanego z danymi indywidualnymi: lub 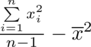(obie wersje są równoważne, w praktyce pierwsza wersja jest częściej używana). Po określeniu wzoru na okazuje się, że w formule pozwalającej wyznaczyć wariancję potrzebna jest wartość średnia 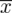, więc to od niej należy zacząć obliczenia.

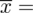
Wzór na średnią z danych indywidualnych wygląda następująco: 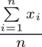. Oczywiście na chłopski rozum średnią można policzyć sumując wszystkie dane, a potem dzieląc przez ilość – jest to jak najbardziej prawidłowe rozwiązanie, a podany wzór oznacza to samo. Jednak zdaję sobie sprawę, że widząc „hieroglify” tego typu wiele osób nie wie co robić, a tym bardziej jak je rozpisywać :). Mając to na uwadze postaram się przybliżyć kwestię podobnych oznaczeń rozpisując je na czynniki pierwsze.

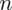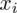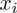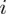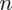Znak to symbol sumy. Pod nim znajduje się zapis , a nad nim , to wartości kolejnych obserwacji. Wszytko razem oznacza, że będziemy dodawać kolejne obserwacje oznaczone symbolem , gdzie będzie rosło od aż do wartości , a więc :

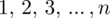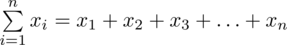
Tak więc średnia po rozpisaniu wygląda następująco:

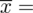
Teraz przełożymy wszystko na dane z zadania. Liczebność próby wynosi , a więc wzór na średnią możemy zapisać następująco:

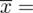
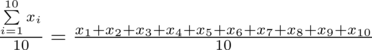
Czym jest 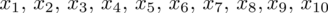? Są to konkretne wyniki z próby, a więc 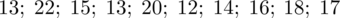. Jeśli ktoś chciałby uporządkować dane indywidualne od najmniejszej do największej, może to spokojnie wykonać. Porządkowanie liczb nie wpływa na wartość średniej, także może zostać tak jak jest. A więc np. .

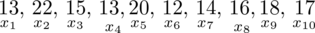Obliczamy średnią:

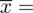
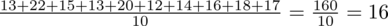
Dysponując wartością liczbową średniej możemy obliczyć wariancję 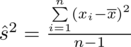. Rozpisanie wzoru wykonujemy analogicznie jak w przypadku średniej. Na początek ogólnie:

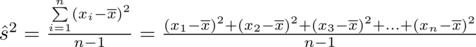
i dla :

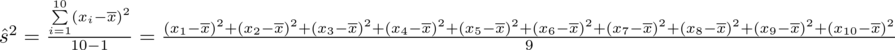
Możemy już podstawiać liczby za 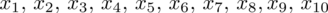, ale proponuję utworzyć tabelkę i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na wariancję z danych indywidualnych, a jej nagłówki zawsze wyglądają tak samo. Na początku od każdej wartości 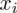odejmujemy średnią, a następnie wynik podnosimy do kwadratu. Sumujemy ostatnią kolumnę (przecięcie wiersza z symbolem i daje kompletny licznik wzoru na wariancję).

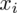
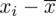
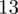
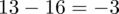
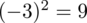
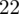
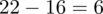
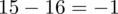
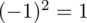
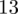
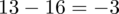
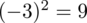
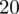
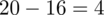
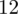
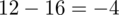
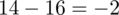
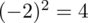
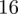
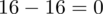
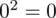
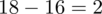
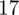
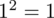
(suma)

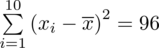
A więc

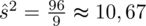
Skoro obliczyliśmy to możemy uzupełnić wzór .

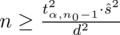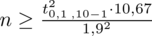
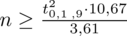
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 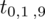oznacza konieczność odnalezienia statystyki dla 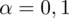i 9 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

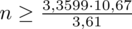
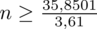
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 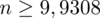, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

Interpretacja brzmi następująco: Aby oszacować średnią zużycia dziennego energii elektrycznej dla populacji rodzin 4-osobowych miasta Z z ufnością 0,9 do próby należy wylosować 10 rodzin, czyli wylosowana próba pilotażowa jest wystarczająca.