Rozkład wielkości stypendiów studenckich jest normalny. Ilu studentów należy wylosować niezależnie do próby, aby przy współczynniku ufności 0,98 zbudować przedział ufności o rozpiętości co najmniej 100 zł dla średniego pobieranego przez nich stypendium? Wiadomo, że zróżnicowanie stypendiów mierzone odchyleniem standardowym jest równe 63 zł.

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Ilu studentów należy wylosować niezależnie do próby, aby przy współczynniku ufności 0,98 zbudować przedział ufności o rozpiętości co najmniej 100 zł dla średniego pobieranego przez nich stypendium? ”

Na początku może się wydawać, że zadanie dotyczy estymacji przedziałowej, ponieważ pojawia się zwrot: zbudować przedział ufności ... . Niemniej jednak przewagę nad tym wyrażeniem zawsze ma: ilu studentów należy wylosować niezależnie do próby .... , czyli szukamy minimalnej liczebności próby. Nie ma również ani słowa o maksymalnym błędzie szacunku, ale jest on ukryty w zadaniu pod innym szyldem. Nie jest to nic nadzwyczajnego, ponieważ zagadnienie minimalnej liczebności próby ściśle wiąże się z estymacją przedziałową. Pojawia się również wyrażenie współczynnik ufności .. Biorąc to pod uwagę mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

“ Rozkład wielkości stypendiów studenckich jest normalny. ”

Rozkład wielkości stypendiów jest rozkładem normalnym i ta wzmianka zawsze odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Na razie nie mamy pełnych informacji na temat tego rozkładu, zatem możemy zapisać symbol 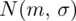, który oznacza, że cecha charakteryzuje się rozkładem normalnym o nieznanej średniej 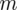i nieznanym odchyleniu standardowym .

“ Ilu studentów należy wylosować niezależnie do próby, aby przy współczynniku ufności 0,98 zbudować przedział ufności o rozpiętości co najmniej 100 zł dla średniego pobieranego przez nich stypendium? ”

Szukamy liczebności próby (liczba studentów), którą oznaczamy literą 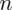. Podano również współczynnik ufności, a więc . Od razu wyznaczamy .

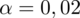Jak pamiętamy, w zadaniach dotyczących minimalnej liczebności próby ważnym elementem jest wartość maksymalnego błędu szacunku 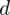. Zamiast tego dowiadujemy się, że przedział ufności powinien mieć rozpiętość przynajmniej 100 zł. Warto zapamiętać, że maksymalny błąd szacunku to połowa przedziału ufności. Jeśli informacja ta wydaje się być zbyt lakoniczna, odsyłam do szerszego wytłumaczenia http://matma-po-ludzku.pl/statystyka/wnioskowanie/estymacja/estymacja_sredniej/zadanie29.php . Otrzymujemy zatem .

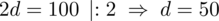Wiadomo, że zróżnicowanie stypendiów mierzone odchyleniem standardowym jest równe 63 zł.

Uzyskujemy także informację, że odchylenie standardowe wielkości stypendiów wynosi 63 zł. Co ważne, nie ma tu żadnej wzmianki, że odchylenie pochodzi z próby. W związku z tym przyjmujemy, że jest to odchylenie standardowe z populacji i oznaczamy je odpowiednio zł.

Skoro zostało podane odchylenie standardowe równe , to możemy wrócić do zapisu dotyczącego normalności rozkładu i go uaktualnić. Zapisujemy symbol 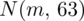, który oznacza, że cecha charakteryzuje się rozkładem normalnym o nieznanej średniej 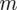i znanym odchyleniu standardowym .

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA studenci	PRÓBA 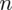wybranych studentów
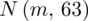- rozkład normalny o nieznanej średniej 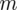i znanym odchyleniu standardowym

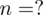
- współczynnik ufności,

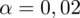
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że jest znana 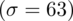, zatem wybieramy model I .

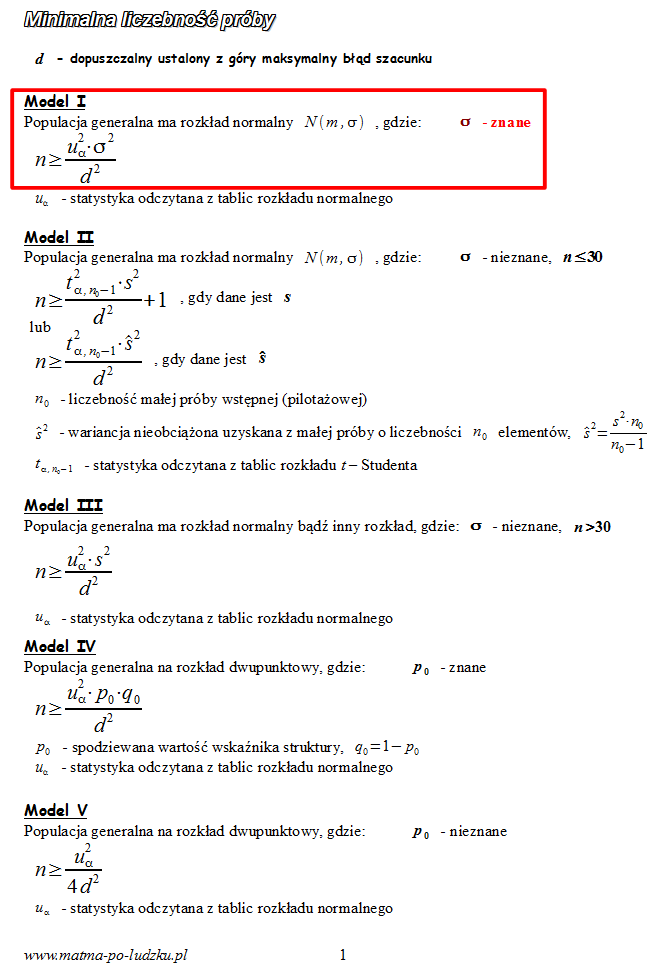
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 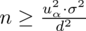konkretnymi liczbami.

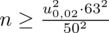
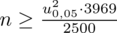
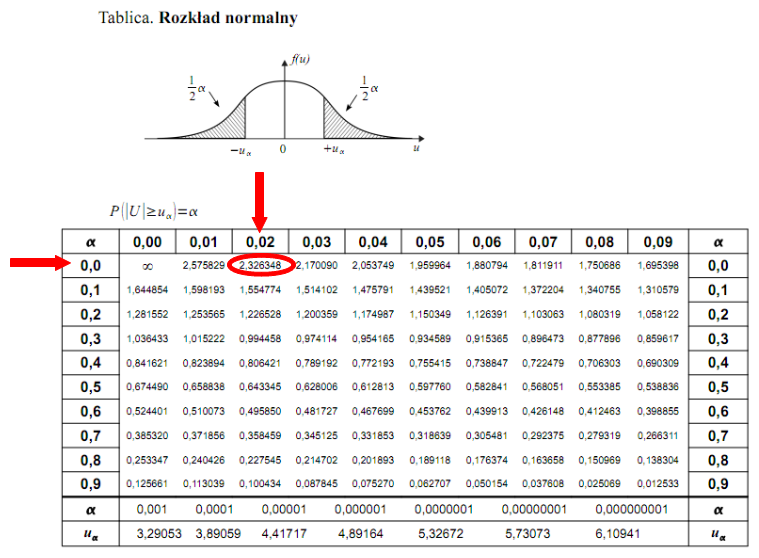
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u , zatem skorzystamy z tablic rozkładu normalnego: http://matma-po-ludzku.pl/materialy/statystyka/wzory/rnormalny.pdf . Zapis 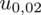oznacza konieczność odnalezienia statystyki dla 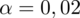. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. 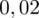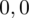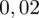W przypadku sumujemy i czyli .

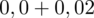Wracamy do obliczeń i podstawiamy 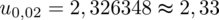(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):

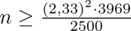
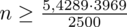
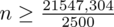
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 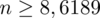, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

Interpretacja brzmi następująco: Aby oszacować średnią wielkość stypendium z ufnością 0,98, do próby należy wylosować 9 studentów.