
Przykład 137
[kliknij aby rozwinąć] 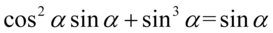
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Daną tożsamość można udowodnić na dwa sposoby.
I sposób
Po prawej stronie, do której uzyskania dążymy mamy tylko sinus, także postaramy się zlikwidować cosinus z lewej strony. Cosinus podniesiony na kwadratu można łatwo zamienić na sinus korzystając z przekształconej jedynki trygonometrycznej  . Wstawiając przekształcenie do przykładu nie zapominajmy o nawiasie:
. Wstawiając przekształcenie do przykładu nie zapominajmy o nawiasie:
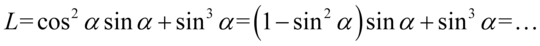
Teraz wymnożymy sinus znajdujący się za nawiasem przez zawartość nawiasu i możemy zredukować składniki:
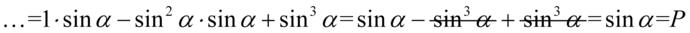
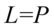
II sposób
Sposób ten wymaga uważnego przyjrzenia się przykładowi. Można tu sprytnie wyciągnąć przed nawias powtarzający się element – czyli sinus i dzięki temu w nawiasie powstanie jedynka trygonometryczna :
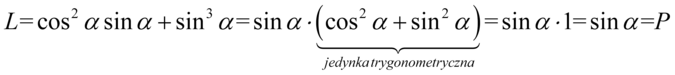
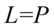
Przykład 138
[kliknij aby rozwinąć] 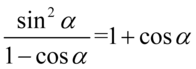
Założenie: 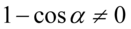 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przeniesieniu jedynki na drugą stronę otrzymujemy
). Po przeniesieniu jedynki na drugą stronę otrzymujemy  i ostatecznie
i ostatecznie 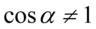 .
.
Daną tożsamość można udowodnić na dwa sposoby.
I sposób
Zajmiemy się lewą stroną, gdzie postaramy się zlikwidować ułamek. Jak widać po lewej stronie występuje tylko cosinus, więc najpierw pozbędziemy się sinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną 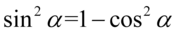 :
:

Teraz najtrudniejsza część. Licznik można potraktować jako wzór skróconego mnożenia 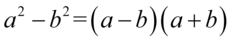 , ponieważ znajdują się w nim dwa elementy oddzielone znakiem odejmowania, a elementy są podniesione do parzystej potęgi. Aby łatwiej dało się zauważyć ten wzór licznik ułamka zapiszemy nieco inaczej, a następnie rozpiszemy korzystając z danego wzoru:
, ponieważ znajdują się w nim dwa elementy oddzielone znakiem odejmowania, a elementy są podniesione do parzystej potęgi. Aby łatwiej dało się zauważyć ten wzór licznik ułamka zapiszemy nieco inaczej, a następnie rozpiszemy korzystając z danego wzoru:
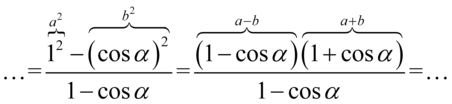
Jak widać w liczniku powstał identyczny nawias jak ten znajdujący się w mianowniku, więc możemy skrócić obydwa:
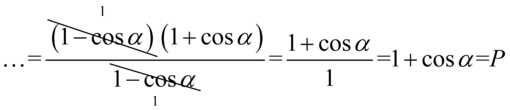
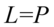
II sposób
Sposób ten jest nietypowy, ponieważ z krótszej prawej strony spróbujemy uzyskać dłuższą lewą stronę, która jest ułamkiem. W celu uzyskania żądanego ułamka wymnożymy prawą stronę przez wyrażenie 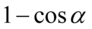 , ale nie wolno zapomnieć, że wymnożenie przez dowolną liczbę lub wyrażenie zmieni wynik. Tak więc aby temu zapobiec musimy podzielić przez to samo wyrażenie, prze które wcześniej wymnożyliśmy np.
, ale nie wolno zapomnieć, że wymnożenie przez dowolną liczbę lub wyrażenie zmieni wynik. Tak więc aby temu zapobiec musimy podzielić przez to samo wyrażenie, prze które wcześniej wymnożyliśmy np. 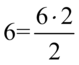 (wymnożyliśmy przez
(wymnożyliśmy przez 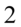 i jednocześnie podzieliśmy przez
i jednocześnie podzieliśmy przez 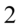 , ale wynik to nadal szóstka):
, ale wynik to nadal szóstka):
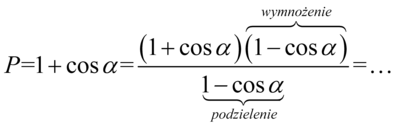
Teraz wystarczy pozbyć się nawiasów na górze wymnażając kolejno składniki lub korzystając ze wzoru skróconego mnożenia 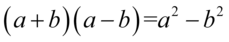 , ponieważ mamy dwa nawiasy różniące się wyłącznie znakiem pośrodku:
, ponieważ mamy dwa nawiasy różniące się wyłącznie znakiem pośrodku:
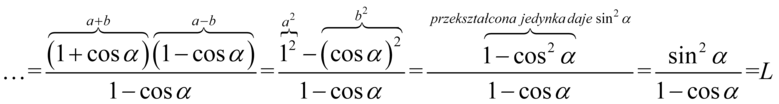
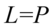
Przykład 139
[kliknij aby rozwinąć] 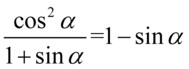
Założenie: 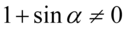 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przeniesieniu jedynki na drugą stronę otrzymujemy ostatecznie
). Po przeniesieniu jedynki na drugą stronę otrzymujemy ostatecznie 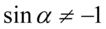 .
.
Daną tożsamość można udowodnić na dwa sposoby.
I sposób
Zajmiemy się lewą stroną, gdzie postaramy się zlikwidować ułamek. Jak widać po lewej stronie występuje tylko sinus, więc najpierw pozbędziemy się cosinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną  :
:
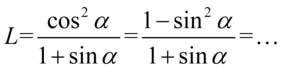
Teraz najtrudniejsza część. Licznik można potraktować jako wzór skróconego mnożenia 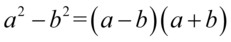 , ponieważ znajdują się w nim dwa elementy oddzielone znakiem odejmowania, a elementy są podniesione do parzystej potęgi. Aby łatwiej dało się zauważyć ten wzór licznik ułamka zapiszemy nieco inaczej, a następnie rozpiszemy korzystając z danego wzoru:
, ponieważ znajdują się w nim dwa elementy oddzielone znakiem odejmowania, a elementy są podniesione do parzystej potęgi. Aby łatwiej dało się zauważyć ten wzór licznik ułamka zapiszemy nieco inaczej, a następnie rozpiszemy korzystając z danego wzoru:
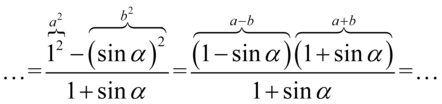
Jak widać w liczniku powstał identyczny nawias jak ten znajdujący się w mianowniku, więc możemy skrócić obydwa:
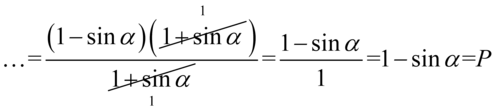
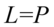
II sposób
Sposób ten jest nietypowy, ponieważ z krótszej prawej strony spróbujemy uzyskać dłuższą lewą stronę, która jest ułamkiem. W celu uzyskania żądanego ułamka wymnożymy prawą stronę przez wyrażenie  , ale nie wolno zapomnieć, że wymnożenie przez dowolną liczbę lub wyrażenie zmieni wynik. Tak więc aby temu zapobiec musimy podzielić przez to samo wyrażenie, prze które wcześniej wymnożyliśmy np.
, ale nie wolno zapomnieć, że wymnożenie przez dowolną liczbę lub wyrażenie zmieni wynik. Tak więc aby temu zapobiec musimy podzielić przez to samo wyrażenie, prze które wcześniej wymnożyliśmy np. 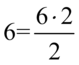 (wymnożyliśmy przez
(wymnożyliśmy przez 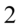 i jednocześnie podzieliśmy przez
i jednocześnie podzieliśmy przez 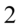 , ale wynik to nadal szóstka):
, ale wynik to nadal szóstka):
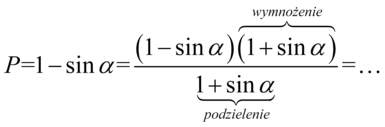
Teraz wystarczy pozbyć się nawiasów na górze wymnażając kolejno składniki lub korzystając ze wzoru skróconego mnożenia 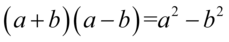 , ponieważ mamy dwa nawiasy różniące się wyłącznie znakiem pośrodku:
, ponieważ mamy dwa nawiasy różniące się wyłącznie znakiem pośrodku:
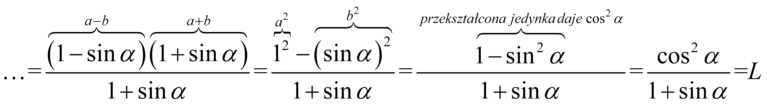
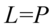
Przykład 140
[kliknij aby rozwinąć] 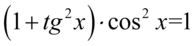
Lewa strona tożsamości jest zdecydowanie dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasów kolejno wymnażając składniki:
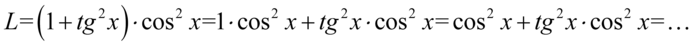
Teraz zapraszam do przykładu o numerze 41, gdzie można śledzić dalszy ciąg przekształceń.