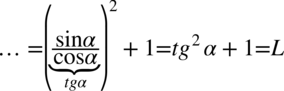Zanim zajmiemy się udowadnianiem tożsamości trygonometrycznych, warto zapoznać się z regułami dotyczącymi upraszczania wyrażeń trygonometrycznych. Zachęcam do przejrzenia: link do upraszczania.
Tożsamość trygonometryczna to równość, w której występują funkcje trygonometryczne. Równość ta jest prawdziwa dla każdego dopuszczalnego kąta (nieważne jaką nazwę ma ten kąt:
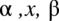 ), dlatego na początku należy podawać założenie, które wyeliminuje przypadki np. dzielenia przez
), dlatego na początku należy podawać założenie, które wyeliminuje przypadki np. dzielenia przez
 .
.
Sprawdzanie, czy wyrażenie jest tożsamością polega na przekształcaniu jednej ze stron równości w taki sposób, aby otrzymać drugą stronę (kierunek: lewa – prawa lub prawa – lewa). Oto kilka w miarę uniwersalnych wskazówek, które pozwolą na sprawne udowadnianie tożsamości:
-
Warto zaczynać przekształcanie tożsamości od dłuższej strony, ponieważ mamy tu określone możliwości manewrowania (dłuższa strona w krótszą) niż w przypadku krótkiego wyrażenia (krótsza strona w dłuższą), gdzie możliwości te są nieograniczone, ale znacznie trudniejsze do wymyślenia.
-
Na początku pozbywamy się nawiasów po danej stronie, wymnażając kolejno składniki lub jeżeli to możliwe korzystając ze wzoru skróconego mnożenia.
-
Po każdym przekształceniu, które wykonamy należy zwracać uwagę, czy nie otrzymaliśmy konkretnego wzoru np. jedynki trygonometrycznej
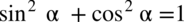 lub jej przekształceń:
lub jej przekształceń:
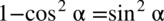 ,
,
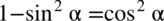 ,
,
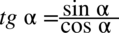 ,
,
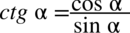 oraz
oraz
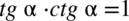 ,
,
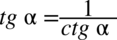 ,
,
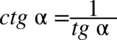 . W przypadku jedynki trygonometrycznej staramy się ją „zwinąć”, a nie rozkładać na sinus i cosinus, bo wyrażenie może się rozrosnąć do ogromnych rozmiarów, oczywiście istnieją wyjątki.
. W przypadku jedynki trygonometrycznej staramy się ją „zwinąć”, a nie rozkładać na sinus i cosinus, bo wyrażenie może się rozrosnąć do ogromnych rozmiarów, oczywiście istnieją wyjątki. -
Przekształcając konkretną stronę cały czas należy zwracać uwagę na to do czego mamy dojść – czyli na drugą stronę tożsamości:
-
jeżeli po przekształcanej stronie występują dwa ułamki, a po drugiej jeden ułamek należy sprowadzić obydwa ułamki do wspólnego mianownika tym samym otrzymując jeden
-
jeżeli po przekształcanej stronie występuje jeden ułamek, a po drugiej stronie dwa to należy je rozdzielić analogicznie jak wykonuje się to na prostszych liczbach np.
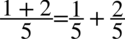
-
jeżeli przekształcana strona zawiera tangensy lub cotangensy, a po stronie, którą mamy otrzymać nie występują to likwidujemy je korzystając ze wzorów
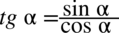 oraz
oraz
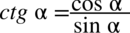 ,
, -
jeżeli przekształcana strona zawiera tangensy lub cotangensy, a po stronie, którą mamy otrzymać występują również wyłącznie tangensy i cotangensy, to nie ma sensu zamieniać je na sinusy i cosinusy (oczywiście istnieje taka możliwość, ale przykład znacznie się skomplikuje), zamieniamy wszystko na tangensy lub cotangensy korzystając ze wzorów
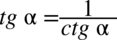 lub
lub
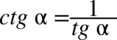 .
.
Czasem pojawia się dylemat dotyczący kolejności postępowania - mianowicie czy najpierw rozkładać jeden ułamek na dwa ułamki czy pozbyć się tangensów lub cotangensów zamieniając je na sinusy i cosinusy. Z reguły najkrótszą drogą jest rozbicie na dwa ułamki, a później likwidacja tangensów lub cotangensów.
Poniżej znajdują się przykłady udowadniania tożsamości trygonometrycznych. Jeżeli ktoś ma inne pomysły na rozwiązania i dają one pożądany wynik, to są one jak najbardziej prawidłowe.
Przykład 1
[kliknij aby rozwinąć]
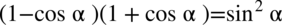
Przykład 2
[kliknij aby rozwinąć]
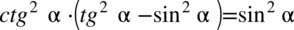
Przykład 3
[kliknij aby rozwinąć]

Przykład 4
[kliknij aby rozwinąć]
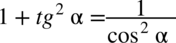
Przykłady – 1 – 5 (red. A. Cewe i H. Nahorska, Matematyka – zbiór zadań dla klasy 1. Kształcenie w zakresie podstawowym, Wydawnictwo Podkowa 2008, str. 23-24, zad. 2.37) ISBN 978-83-88299-37-7
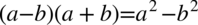 .
. 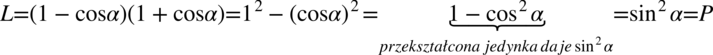

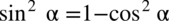 , a lewa strona składa się z
, a lewa strona składa się z
 i cosinusów, co jest nam na rękę.
i cosinusów, co jest nam na rękę.
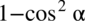 można zapisać jako
można zapisać jako
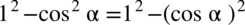 (jedynka podniesiona do kwadratu to nadal jeden), a taka forma umożliwia nam rozkład tego wyrażenia ze wzoru skróconego mnożenia
(jedynka podniesiona do kwadratu to nadal jeden), a taka forma umożliwia nam rozkład tego wyrażenia ze wzoru skróconego mnożenia
 :
:

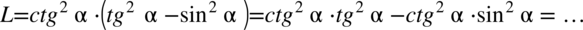
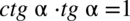 oraz zamienimy cotangens na sinus zgodnie ze wzorem
oraz zamienimy cotangens na sinus zgodnie ze wzorem
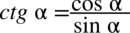 , ponieważ po prawej stronie występuje wyłącznie sinus i nie ma tu ani tangensów, ani cotangensów. Aby zapisać
, ponieważ po prawej stronie występuje wyłącznie sinus i nie ma tu ani tangensów, ani cotangensów. Aby zapisać
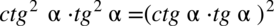 skorzystamy z własności potęg
skorzystamy z własności potęg
 , z tego wzoru można korzystać jedynie w przypadku gdy wykładniki potęg są takie same (w przykładzie były to
, z tego wzoru można korzystać jedynie w przypadku gdy wykładniki potęg są takie same (w przykładzie były to
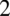 ) i pomiędzy kolejnymi liczbami jest znak mnożenia lub dzielenia.
) i pomiędzy kolejnymi liczbami jest znak mnożenia lub dzielenia.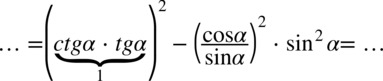
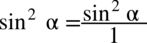 (każda liczba podzielona przez
(każda liczba podzielona przez
 to nadal ta sama liczba), ponieważ wiele osób ma problemy z prawidłowym skracaniem ułamków, a wykonywanie działań w przekształcaniu tożsamości wykonuje się identycznie jak działania na ułamkach zwykłych.
to nadal ta sama liczba), ponieważ wiele osób ma problemy z prawidłowym skracaniem ułamków, a wykonywanie działań w przekształcaniu tożsamości wykonuje się identycznie jak działania na ułamkach zwykłych.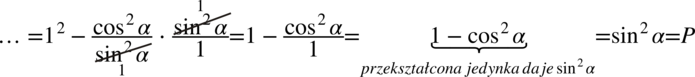

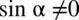 (mianownik nie może być równy
(mianownik nie może być równy
 )
)
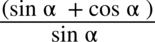
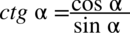 :
: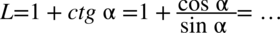
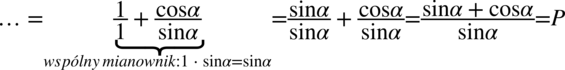

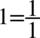 , bo każda liczba podzielona przez
, bo każda liczba podzielona przez
 nie ulega zmianie.
nie ulega zmianie. 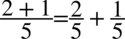 i skorzystać ze wzoru
i skorzystać ze wzoru
 :
: 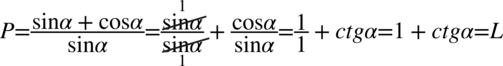

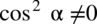 (mianownik nie może być równy
(mianownik nie może być równy
 )
) 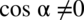 , bo jeżeli cosinus będzie wynosił
, bo jeżeli cosinus będzie wynosił
 , to także cosinus do kwadratu będzie równy
, to także cosinus do kwadratu będzie równy
 ) .
) .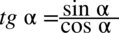 , ponieważ po prawej stronie równości nie występuje.
, ponieważ po prawej stronie równości nie występuje. 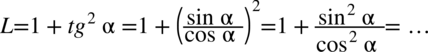
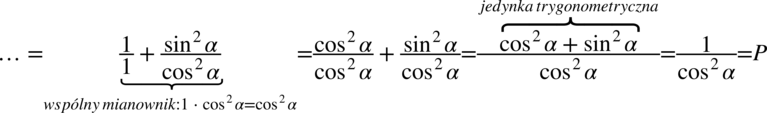

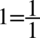 , bo każda liczba podzielona przez
, bo każda liczba podzielona przez
 nie ulega zmianie.
nie ulega zmianie. 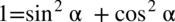 . Z rozkładaniem liczby
. Z rozkładaniem liczby
 zgodnie ze wzorem na „jedynkę trygonometryczną” należy postępować ostrożnie, ponieważ pochopne użycie tego wzoru może bardzo skomplikować przykład (zwłaszcza długi), dlatego warto robić to dopiero w ostateczności. Jednak w tym przypadku przykład jest krótki, zatem nie będzie większego problemu. Na początku rozdzielimy ułamek na dwa mniejsze
zgodnie ze wzorem na „jedynkę trygonometryczną” należy postępować ostrożnie, ponieważ pochopne użycie tego wzoru może bardzo skomplikować przykład (zwłaszcza długi), dlatego warto robić to dopiero w ostateczności. Jednak w tym przypadku przykład jest krótki, zatem nie będzie większego problemu. Na początku rozdzielimy ułamek na dwa mniejsze
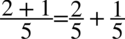 i skorzystamy z odpowiednich wzorów
i skorzystamy z odpowiednich wzorów
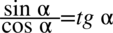 :
: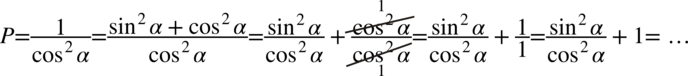
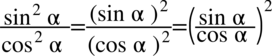 skorzystamy z własności potęg
skorzystamy z własności potęg
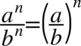 - z tego wzoru można korzystać jedynie w przypadku gdy wykładniki potęg są takie same (w przykładzie były to
- z tego wzoru można korzystać jedynie w przypadku gdy wykładniki potęg są takie same (w przykładzie były to
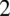 ) i pomiędzy kolejnymi liczbami jest znak mnożenia lub dzielenia.
) i pomiędzy kolejnymi liczbami jest znak mnożenia lub dzielenia.