Upraszczanie wyrażeń trygonometrycznych często bywa problem. Postaram się podać kilka w miarę uniwersalnych wskazówek, które pomogą sprytnie dokonać przekształceń.
Podstawa to znajomość wzorów:
- „jedynka trygonometryczna”
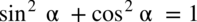 (starajmy się raczej zwijać do
(starajmy się raczej zwijać do
 , a nie rozkładać ją na
, a nie rozkładać ją na
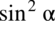 i
i
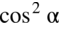 , bo przykład zamiast się uprościć rozbuduje się – wykonujmy rozbijanie w ostateczności, gdy nie mamy innego pomysłu)
, bo przykład zamiast się uprościć rozbuduje się – wykonujmy rozbijanie w ostateczności, gdy nie mamy innego pomysłu)
oraz jej przekształcenia czyli
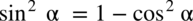 lub
lub
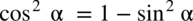 . Jeżeli zatem w przykładzie pojawi się
. Jeżeli zatem w przykładzie pojawi się
 lub
lub
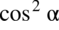 to będzie można zapisać oba wyrażenia używając przekształceń jedynki trygonometrycznej:
to będzie można zapisać oba wyrażenia używając przekształceń jedynki trygonometrycznej:
-
iloczyn tangensa i cotangensa tego samego kąta zawsze wynosi
 :
:
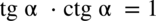
Przekształcenia wzoru
 oraz
oraz 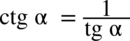 gdy będziemy potrzebowali zapisać tangens za pomocą cotangensa lub odwrotnie.
gdy będziemy potrzebowali zapisać tangens za pomocą cotangensa lub odwrotnie. -
zamiana tangensa i cotangensa na sinus i cosinus:
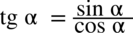 oraz
oraz 
Kolejna kwestia to zapisy 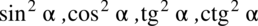
Warto pamiętać:
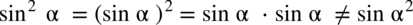
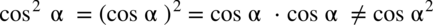
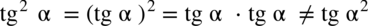
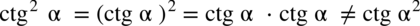
Trzy pierwsze zapisy w każdym przypadku są równoważne, ale już trzeci nie, bo gdy zapomnimy/ nie napiszemy nawiasu to nie podniesiemy samego sinusa / cosinusa / tangensa / cotangensa do potęgi, ale kąt 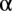 . Podobnie ma się sprawa z zapisem jakichkolwiek innych potęg.
. Podobnie ma się sprawa z zapisem jakichkolwiek innych potęg.
Działania na funkcjach trygonometrycznych przypominają do złudzenia operacje na ułamkach (zwłaszcza gdy pojawiają się kreski ułamkowe) i wyrażeniach algebraicznych. Można je dodawać, odejmować, mnożyć, dzielić, skracać.
Przykłady dodawania i odejmowania:
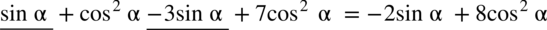
analogicznie jak przy normalnych wyrażeniach algebraicznych:
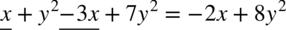
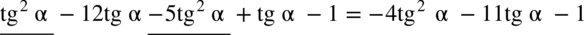
analogicznie jak przy zwykłych wyrażeniach algebraicznych:
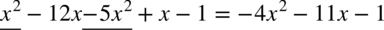
Tak więc tangens do kwadratu to nie to samo co sam tangens, tak jak  i
i 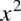 , dotyczy to też innych funkcji trygonometrycznych.
, dotyczy to też innych funkcji trygonometrycznych.
Przykłady mnożenia i dzielenia:

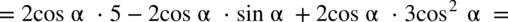
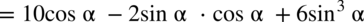
analogicznie jak na zwyczajnych wyrażeniach algebraicznych:
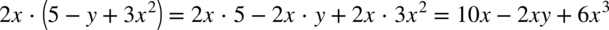

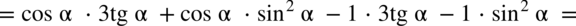
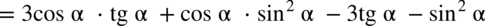
analogicznie jak na zwyczajnych wyrażeniach algebraicznych:
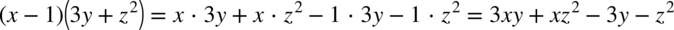


Czasami pojawia się również problem zapisu różnych działań, w których pojawiają się kreski ułamkowe np. przy mnożeniu lub dzieleniu wtedy bardzo pomaga zapis  , ponieważ jakakolwiek liczba podzielona przez
, ponieważ jakakolwiek liczba podzielona przez  nie ulega zmianie. Dzięki temu wiemy jakie składniki mamy wymnożyć, bo widać co jest na górze, a co na dole.
nie ulega zmianie. Dzięki temu wiemy jakie składniki mamy wymnożyć, bo widać co jest na górze, a co na dole.
Przykłady:
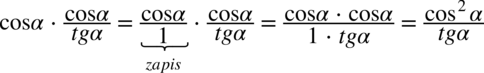
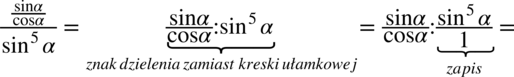
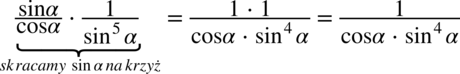
Wreszcie ostatnia sprawa do wyjaśnienia to sprowadzanie do wspólnego mianownika dwóch ułamków złożonych z funkcji trygonometrycznych.
Wykonuje się to tak jak na zwykłych liczbach – a więc na początku najprościej zrobimy mnożąc mianowniki z obydwu ułamków :
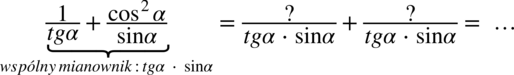
Mamy już wspólny mianownik, teraz oczywiście trzeba uzupełnić liczniki w nowych ułamkach.
Najprościej można zrobić to w następujący sposób – najpierw przepisujemy liczniki ze starych ułamków

i porównujemy stary mianownik z nowym mianownikiem każdego ułamka zastanawiając się jaki składnik jest nowy:
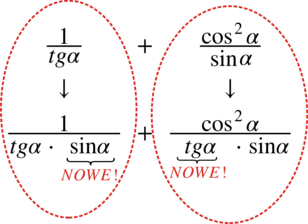
Przedostatni etap to domnożenie każdego nowego elementu z mianownika w liczniku w każdym z ułamków:

To tak jak z małymi dziećmi, skoro jednemu dasz nową zabawkę to drugie też musi dostać identyczną aby nie było kłótni i awantur. Nasze dzieci mają nietypowe imiona Mianownik i Licznik ;).
Ostatni etap to zapisanie wszystkiego na jednej kresce ułamkowej:
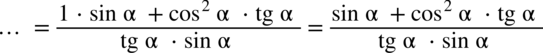
I na koniec w miarę uniwersalna instrukcja obsługi pozwalająca upraszczać wyrażenia trygonometryczne. Czytamy po kolei i wprowadzamy w życie.
-
Na samym początku - jeżeli w przykładzie występują nawiasy to należy się ich pozbyć poprzez wymnożenie składników lub jeżeli jest to wzór skróconego mnożenia należy skorzystać z odpowiedniego wzoru.
-
Jeżeli w przykładzie nie ma nawiasów lub właśnie się ich pozbyliśmy to zawsze sprawdzamy czy nie otrzymaliśmy konkretnych wzorów o których wspomniano na samym początku, a więc jedynka trygonometryczna lub jej przekształcenia itp.
-
Zawsze po każdym przekształceniu sprawdzamy czy nie otrzymaliśmy wzorów podanych na początku.
-
Jeżeli w przykładzie występują tangensy lub cotangensy wraz z sinusami lub cosinusami to korzystamy ze wzorów
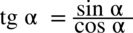 oraz
oraz  aby się ich pozbyć. Jeżeli występują same tangensy i cotangensy to nie rozbijamy ich na sinusy lub cosinusy – korzystamy raczej ze wzorów
aby się ich pozbyć. Jeżeli występują same tangensy i cotangensy to nie rozbijamy ich na sinusy lub cosinusy – korzystamy raczej ze wzorów  oraz
oraz 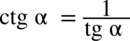 . Decydujemy się: albo wszystko zamieniamy na tangensy albo na cotangensy.
. Decydujemy się: albo wszystko zamieniamy na tangensy albo na cotangensy. -
Gdy w przykładzie występują kreski ułamkowe czyli ułamki lub gdy pojawiają one po zamianie tangensów lub cotangensów na sinusy lub cosinusy to wszystkie nowo powstałe ułamki trzeba wbić na jedną kreskę, a więc sprowadzić do wspólnego mianownika.
-
W sytuacji gdy nie możemy zastosować poprzednich punktów być może trzeba powtarzający się element wyciągnąć przed nawias, wówczas być może w nawiasie otrzymamy jeden z podstawowych wzorów. Jeżeli nie zadziała to być może trzeba pomyśleć o ukrytym w przykładzie wzorze skróconego mnożenia.
-
Gdy nie zadziała żaden z poprzednich punktów to przykład wymaga zastanowienia i kombinowania. Z reguły nietypowe przykłady wymagają wprawy w upraszczaniu, a więc pozostaje ćwiczenie :).
Przykład 1
[kliknij aby rozwinąć] 
Przykład 2
[kliknij aby rozwinąć] 
Przykład 3
[kliknij aby rozwinąć] 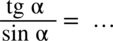
Przykład 4
[kliknij aby rozwinąć] 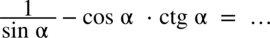
Przykład 5
[kliknij aby rozwinąć] 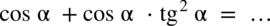
Przykład 6
[kliknij aby rozwinąć] 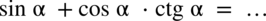
Przykład 7
[kliknij aby rozwinąć] 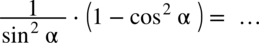
Przykład 8
[kliknij aby rozwinąć] 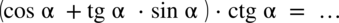
Przykład 9
[kliknij aby rozwinąć] 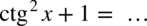
Przykład 10
[kliknij aby rozwinąć] 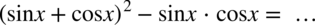
Przykład 11
[kliknij aby rozwinąć] 
Przykład 12
[kliknij aby rozwinąć] 
Przykład 13
[kliknij aby rozwinąć] 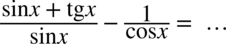
Przykład 14
[kliknij aby rozwinąć] 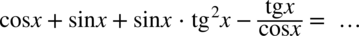
Przykład 15
[kliknij aby rozwinąć] 
Przykład 16
[kliknij aby rozwinąć] 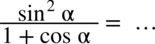
Przykład 17
[kliknij aby rozwinąć] 
Przykład 18
[kliknij aby rozwinąć] 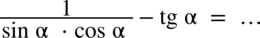
Przykład 19
[kliknij aby rozwinąć] 
Przykład 20
[kliknij aby rozwinąć] 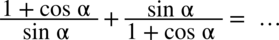
Przykład 21
[kliknij aby rozwinąć] 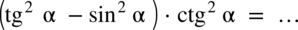
Przykład 22
[kliknij aby rozwinąć] 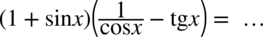
Przykład 23
[kliknij aby rozwinąć] 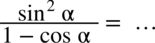
Przykład 24
[kliknij aby rozwinąć] 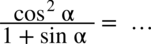
Przykład 25
[kliknij aby rozwinąć] 
Przykład 26
[kliknij aby rozwinąć] 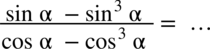
Przykład 27
[kliknij aby rozwinąć] 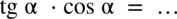
Przykład 28
[kliknij aby rozwinąć] 
Przykład 29
[kliknij aby rozwinąć] 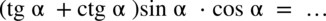
Przykład 30
[kliknij aby rozwinąć] 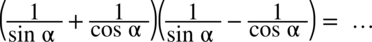
Przykład 31
[kliknij aby rozwinąć] 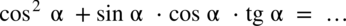
Przykład 32
[kliknij aby rozwinąć] 
Przykład 33
[kliknij aby rozwinąć] 
Przykład 34
[kliknij aby rozwinąć] 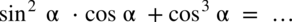
Przykład 35
[kliknij aby rozwinąć] 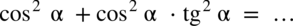
Przykład 36
[kliknij aby rozwinąć] 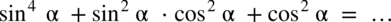
Przykład 37
[kliknij aby rozwinąć] 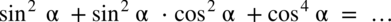
Przykład 38
[kliknij aby rozwinąć] 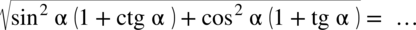
Przykład 39
[kliknij aby rozwinąć] 
Przykład 40
[kliknij aby rozwinąć] 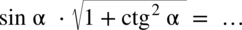
Przykład 41
[kliknij aby rozwinąć] 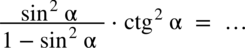
Przykład 42
[kliknij aby rozwinąć] 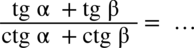
Przykład 43
[kliknij aby rozwinąć] 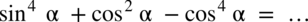
Przykład 44
[kliknij aby rozwinąć] 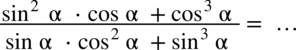
Przykład 45
[kliknij aby rozwinąć] 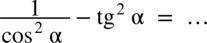
Przykład 46
[kliknij aby rozwinąć] 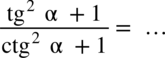
Przykład 47
[kliknij aby rozwinąć] 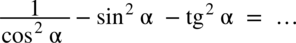
Przykład 48
[kliknij aby rozwinąć] 
Przykład 49
[kliknij aby rozwinąć] 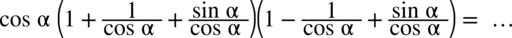
Przykład 50
[kliknij aby rozwinąć] 
Przykład 51
[kliknij aby rozwinąć] 
Przykład 52
[kliknij aby rozwinąć] 
Przykłady 1-8 pochodzą ze str. 134 - Matematyka kl.1 autorstwa: Krzysztof Kłaczkow, Marcin Kurczab,Elżbieta Świda,ISBN 9788389023384,Oficyna Edukacyjna Krzysztof Pazdro 2006
Przykłady 9-14 pochodzą ze str. 148 - Matematyka 1. Zakresy podstawowy i rozszerzony. Zbiór zadań dla liceum ogólnokształcącego, liceum profilowanego i technikum autorstwa: Piotr Pyrdoł,ISBN: 9788373901434,Operon Wydawnictwo Pedagogiczne 2003
Przykłady 15 – 52 pochodza ze str. 11-113 - Matematyka 1. Zakresy podstawowy i rozszerzony. Zbiór zadań dla liceum ogólnokształcącego, liceum profilowanego i technikum. Linia 1 ponadstandardowa. autorstwa: Pawłowski Henryk,ISBN 9788373901140,Operon Wydawnictwo Pedagogiczne 2005
 i otrzymujemy:
i otrzymujemy: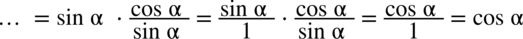
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez
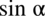 przed nawias:
przed nawias: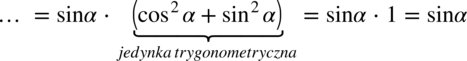
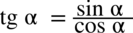 :
: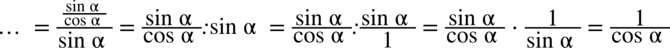
 , ponieważ jakakolwiek liczba podzielona przez
, ponieważ jakakolwiek liczba podzielona przez 
 i otrzymujemy:
i otrzymujemy: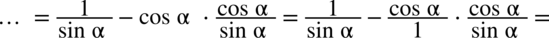

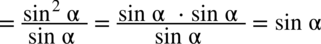
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez 
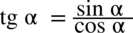 :
: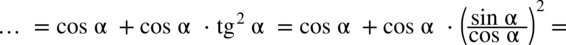


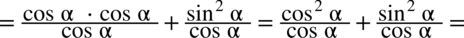
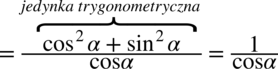


 otrzymując:
otrzymując: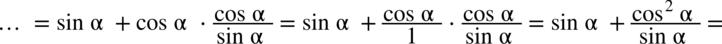
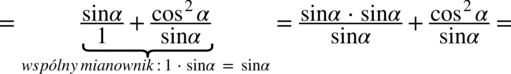

 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez
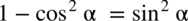 , zatem otrzymujemy:
, zatem otrzymujemy: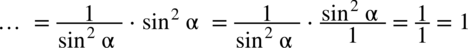
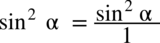 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez
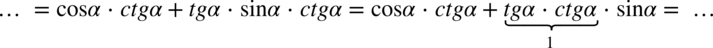
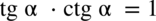 , teraz skorzystamy ze wzoru
, teraz skorzystamy ze wzoru  w celu pozbycia się cotangensa:
w celu pozbycia się cotangensa: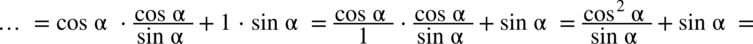
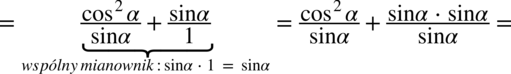
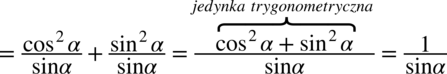
 oraz
oraz  , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez
 :
: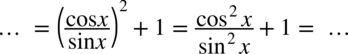
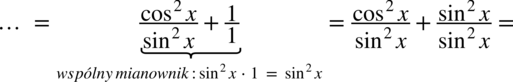
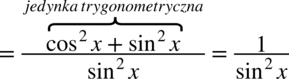
 , gdzie
, gdzie 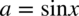 oraz
oraz  :
:
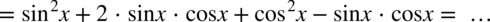
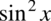 i
i 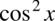 to warto napisać je obok siebie o ile oczywiście jest to możliwe. Dokonamy również redukcji wyrazów podobnych:
to warto napisać je obok siebie o ile oczywiście jest to możliwe. Dokonamy również redukcji wyrazów podobnych: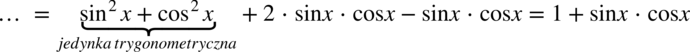
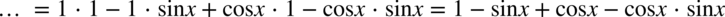
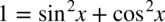 i tak nic nie da, zatem mamy już ostateczny wynik.
i tak nic nie da, zatem mamy już ostateczny wynik. :
: 
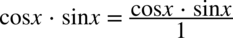 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie:
nie ulega zmianie: 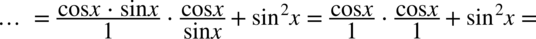
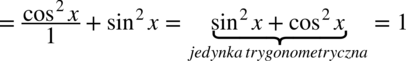
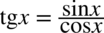 :
: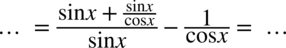
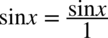 :
:

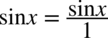 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie :
nie ulega zmianie : 

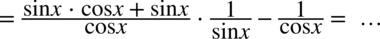
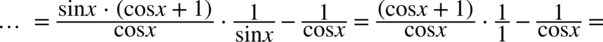


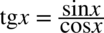 :
: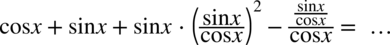
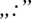 i zamieniając dzielenie na mnożenie:
i zamieniając dzielenie na mnożenie:
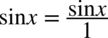 oraz
oraz  :
:
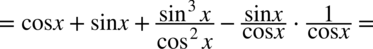
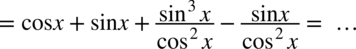
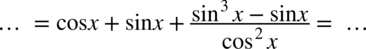
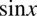 przed nawias, bo nie możemy inaczej postąpić, a tym bardziej odjąć zmiennych o różnych potęgach:
przed nawias, bo nie możemy inaczej postąpić, a tym bardziej odjąć zmiennych o różnych potęgach:
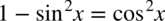 - niestety nie zgadzają się nam znaki. Przepis jest prosty w takich przypadkach należy wyciągnąć minus przez nawias, co zmieni znaki w nawiasie na przeciwne. Dla wygody wrzucimy wyciągnięty minus przed
- niestety nie zgadzają się nam znaki. Przepis jest prosty w takich przypadkach należy wyciągnąć minus przez nawias, co zmieni znaki w nawiasie na przeciwne. Dla wygody wrzucimy wyciągnięty minus przed 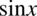 :
:



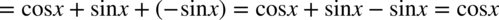
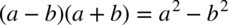 . Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
. Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
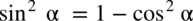 :
:
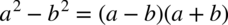 i na końcu skrócić:
i na końcu skrócić: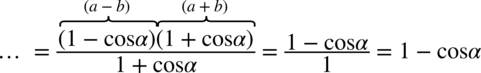
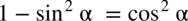
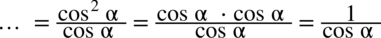
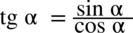 i spróbujemy stworzyć jeden ułamek sprowadzając oba wyrażenia do wspólnego mianownika:
i spróbujemy stworzyć jeden ułamek sprowadzając oba wyrażenia do wspólnego mianownika: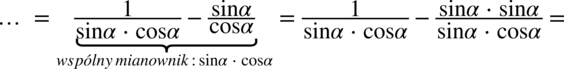
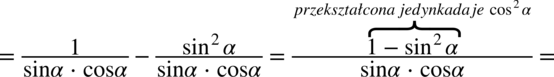
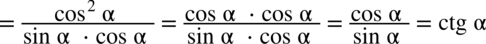
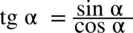 i spróbujemy stworzyć jeden ułamek sprowadzając oba wyrażenia do wspólnego mianownika:
i spróbujemy stworzyć jeden ułamek sprowadzając oba wyrażenia do wspólnego mianownika:

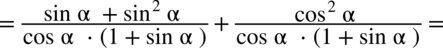
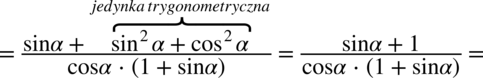
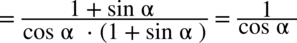
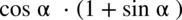 nie został wymnożony, warto z tym zaczekać, ponieważ czasem takie postępowanie powoduje, że często nie zauważamy możliwości skracania w nowo powstałym mianowniku. Dzięki temu w końcówce przykładu bezproblemowo skrócono licznik z mianownikiem.
nie został wymnożony, warto z tym zaczekać, ponieważ czasem takie postępowanie powoduje, że często nie zauważamy możliwości skracania w nowo powstałym mianowniku. Dzięki temu w końcówce przykładu bezproblemowo skrócono licznik z mianownikiem.
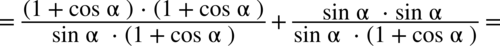

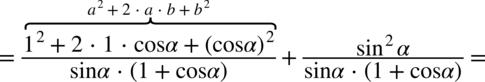

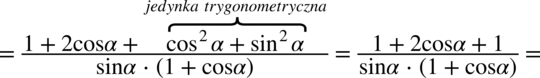
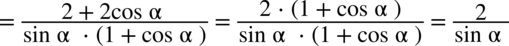
 nie został wymnożony, warto z tym zaczekać, ponieważ czasem zbyt szybkie pozbycie się nawiasów w nowo powstałym mianowniku powoduje, że często nie zauważamy możliwości skracania. Dzięki temu w końcówce przykładu po wyciągnięciu
nie został wymnożony, warto z tym zaczekać, ponieważ czasem zbyt szybkie pozbycie się nawiasów w nowo powstałym mianowniku powoduje, że często nie zauważamy możliwości skracania. Dzięki temu w końcówce przykładu po wyciągnięciu 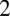 przed nawias bezproblemowo skrócono licznik z mianownikiem.
przed nawias bezproblemowo skrócono licznik z mianownikiem.
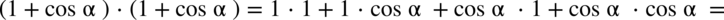
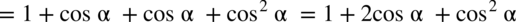
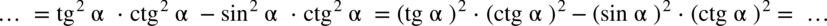
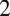 ) można zastosować wzór
) można zastosować wzór  :
: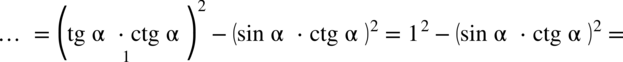
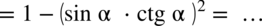
 :
:

 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma wątpliwości, jak należy skracać ułamki.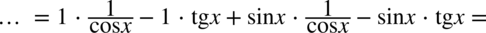
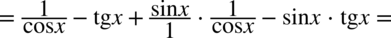
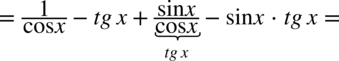
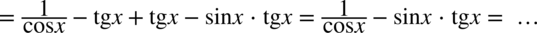
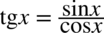 :
:
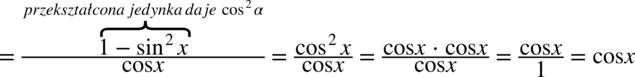
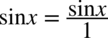 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma wątpliwości, jak należy wymnażać ułamki.
nie ulega zmianie, przy takim zapisie nie ma wątpliwości, jak należy wymnażać ułamki.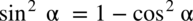 :
: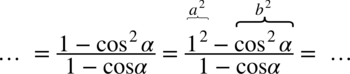
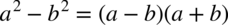 i na końcu skrócić:
i na końcu skrócić:
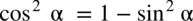 :
: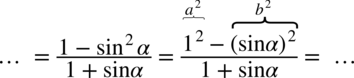
 i na końcu skrócić:
i na końcu skrócić:
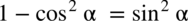
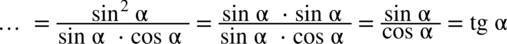
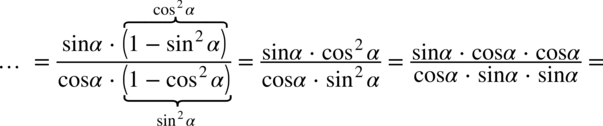
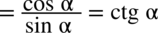
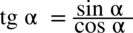 :
: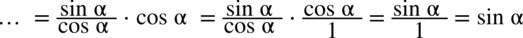
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.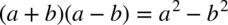 . Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
. Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
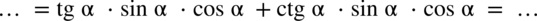
 oraz
oraz  :
: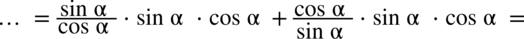
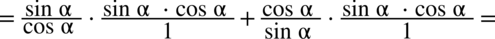
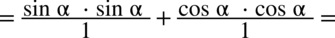
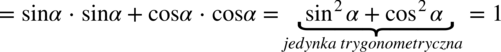
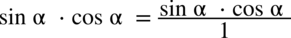 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki. . Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
. Oczywiście nic się nie stanie, jeżeli nie zauważymy tego wzoru, można po prostu wymnażać kolejno składniki – i tak otrzymamy to samo.
 z licznika w obu ułamkach korzystając z tradycyjnej jedynki trygonometrycznej
z licznika w obu ułamkach korzystając z tradycyjnej jedynki trygonometrycznej 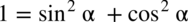 :
: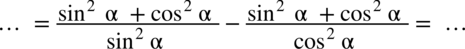
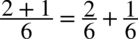 :
: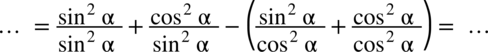
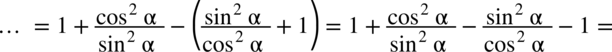
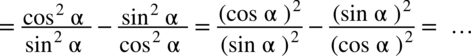
 ) można zastosować wzór
) można zastosować wzór 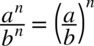 :
: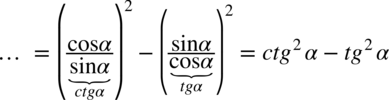
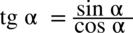 :
: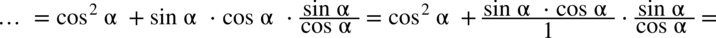
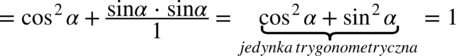
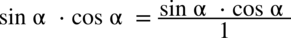 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.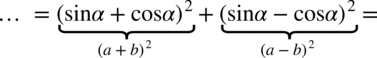
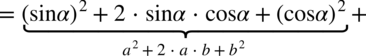
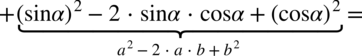
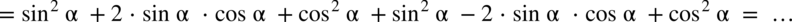
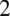 przed nawias:
przed nawias:
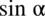 . Należy sprawdzać, czy to się opłaca:
. Należy sprawdzać, czy to się opłaca: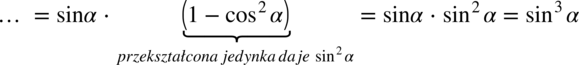
 przed nawias, ponieważ ten element się powtarza:
przed nawias, ponieważ ten element się powtarza: 
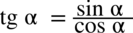 :
: 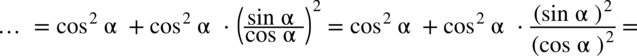
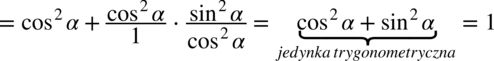
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.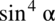 grupując w nawias dwa pierwsze elementy co nic nie zmieni w wartości wyrażenia:
grupując w nawias dwa pierwsze elementy co nic nie zmieni w wartości wyrażenia: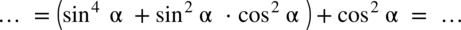
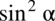 :
:
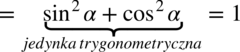
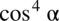 grupując w nawias dwa ostatnie elementy co nic nie zmieni w wartości wyrażenia:
grupując w nawias dwa ostatnie elementy co nic nie zmieni w wartości wyrażenia: 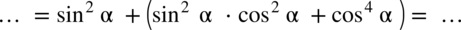
 :
: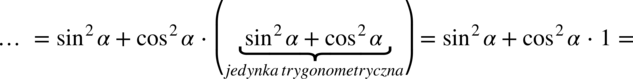
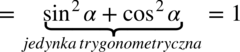
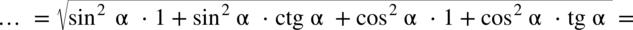
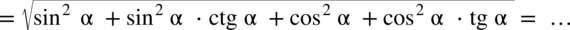
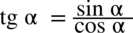 oraz
oraz  :
: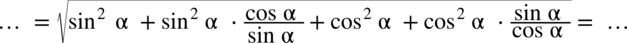
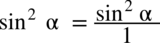 oraz
oraz 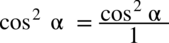 i skracamy:
i skracamy:
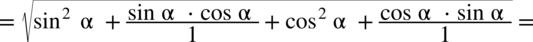
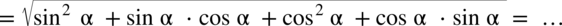
 , bo mnożenia jest przemienne tak jak
, bo mnożenia jest przemienne tak jak 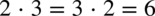 :
: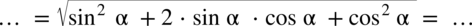
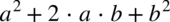 i „zwinięcie” go do postaci
i „zwinięcie” go do postaci 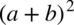 :
:
 (jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy:
(jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy: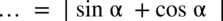

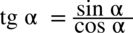 :
: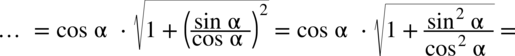
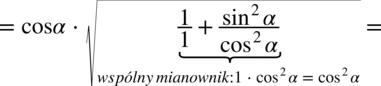
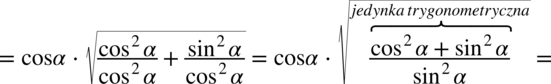

 :
: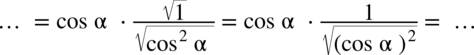
 (jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy:
(jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy: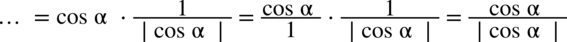
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
 :
: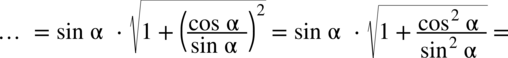
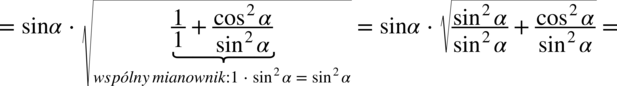
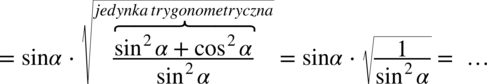
 :
:
 (jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy:
(jeżeli wyciągam pierwiastek kwadratowy z jakiegokolwiek wyrażenia podniesionego do kwadratu to otrzymujemy moduł z tego wyrażenia) otrzymujemy: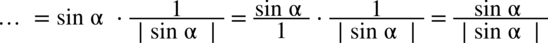
 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.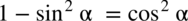 :
: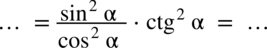
 :
: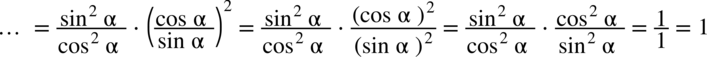
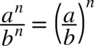 dzięki czemu w nawiasie otrzymamy tangens:
dzięki czemu w nawiasie otrzymamy tangens: 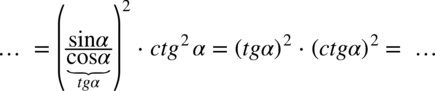
 :
: 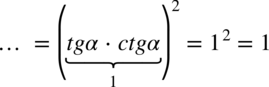
 oraz
oraz  (można też zamienić cotangensy na tangensy) i powstałe w liczniku ułamki sprowadzić do wspólnego mianownika:
(można też zamienić cotangensy na tangensy) i powstałe w liczniku ułamki sprowadzić do wspólnego mianownika:
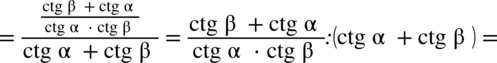
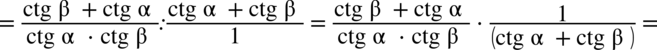
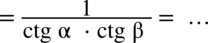

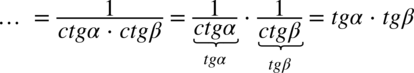
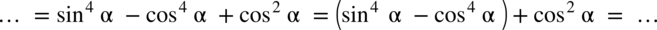
 . Aby go zobaczyć wyrażenie w nawiasie zostanie przekształcone:
. Aby go zobaczyć wyrażenie w nawiasie zostanie przekształcone: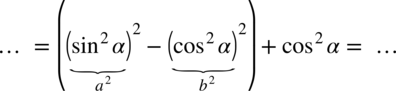
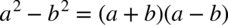 :
:
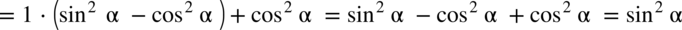
 , a w mianowniku
, a w mianowniku 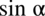 :
: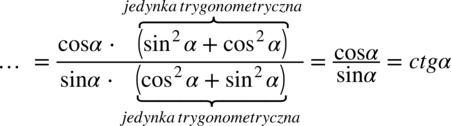
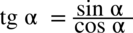 :
: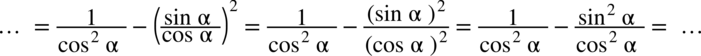
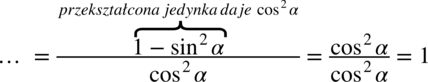
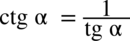 , można też postąpić odwrotnie zamieniając cotangens na tangens – oba sposoby są jak najbardziej prawidłowe i wymagają tyle samo czasu, ważne jest tylko aby w przykładzie była tylko jedna z tych funkcji.
, można też postąpić odwrotnie zamieniając cotangens na tangens – oba sposoby są jak najbardziej prawidłowe i wymagają tyle samo czasu, ważne jest tylko aby w przykładzie była tylko jedna z tych funkcji.
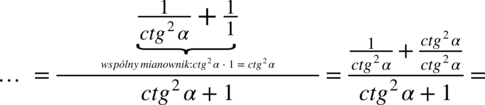

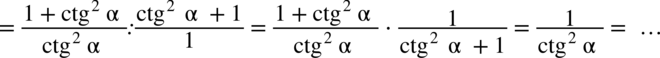
 (
(  ):
):
 oraz
oraz 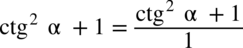 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.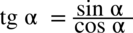 :
: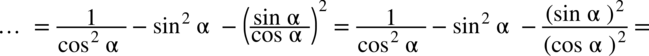
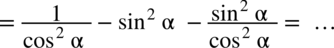


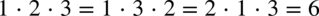 . Pamiętajmy o zapisaniu pierwszego wyniku w nawiasie, dopiero później wymnożymy pozostały nawias.
. Pamiętajmy o zapisaniu pierwszego wyniku w nawiasie, dopiero później wymnożymy pozostały nawias. 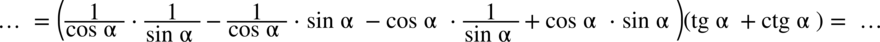
 oraz
oraz  , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.):
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.):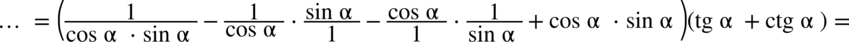
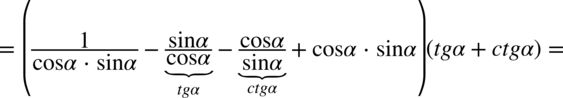
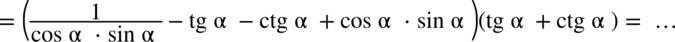
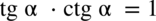 . Oczywiście nic się nie stanie jeżeli tego nie zauważymy i w drugim nawiasie tangens i cotangens zamienimy ze wzorami
. Oczywiście nic się nie stanie jeżeli tego nie zauważymy i w drugim nawiasie tangens i cotangens zamienimy ze wzorami 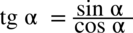 oraz
oraz  . Ja wykonam to nieco później o ile będzie niezbędne. Na razie jednak wymnażam pozostałe nawiasy:
. Ja wykonam to nieco później o ile będzie niezbędne. Na razie jednak wymnażam pozostałe nawiasy: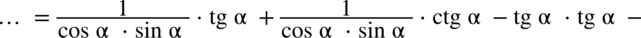
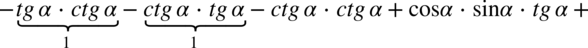

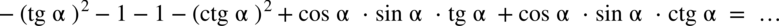
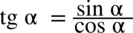 oraz
oraz  .
. 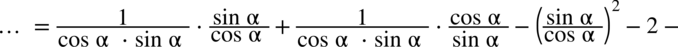

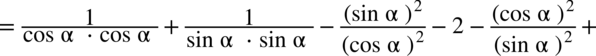
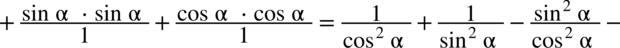
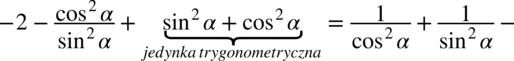

 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.)
nie ulega zmianie, przy takim zapisie nie ma również wątpliwości, jak należy skracać ułamki.)

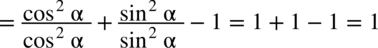
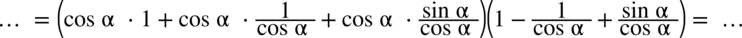
 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie) .
nie ulega zmianie) . 
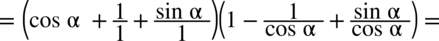
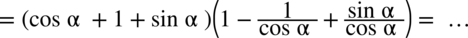
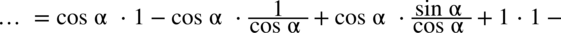

 oraz
oraz  :
: 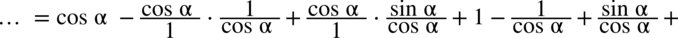
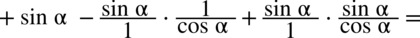


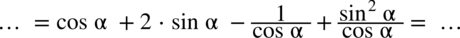
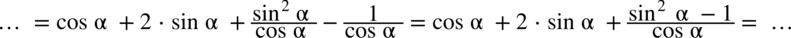
 oraz
oraz  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):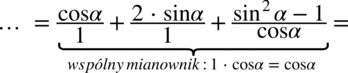
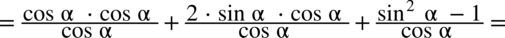
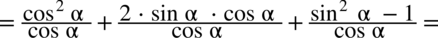

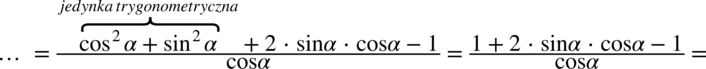
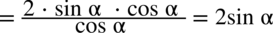
 przed nawias, natomiast w liczniku rozbijemy
przed nawias, natomiast w liczniku rozbijemy 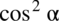 korzystając z przekształconej jedynki trygonometrycznej – czyli
korzystając z przekształconej jedynki trygonometrycznej – czyli 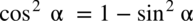 :
: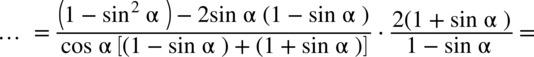
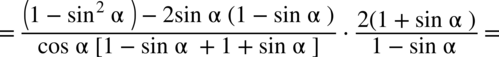
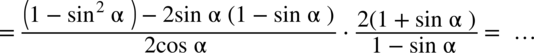
 z zredukowanego mianownika i
z zredukowanego mianownika i 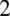 z licznika mniejszego ułamka. Oczywiście w mianowniku „dużego” ułamka można było także powymnażać kolejne nawiasy przez
z licznika mniejszego ułamka. Oczywiście w mianowniku „dużego” ułamka można było także powymnażać kolejne nawiasy przez  zamiast wyciągania przed nawias – i tak otrzymalibyśmy to samo.
zamiast wyciągania przed nawias – i tak otrzymalibyśmy to samo.
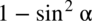 na iloczyn dwóch nawiasów zgodnie ze wzorem skróconego mnożenia
na iloczyn dwóch nawiasów zgodnie ze wzorem skróconego mnożenia 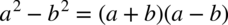 :
: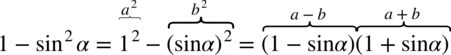
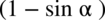 , który przed chwilą stworzyliśmy korzystając ze wzoru skróconego mnożenia. Dzięki temu będziemy mogli wyciągnąć przed nawias właśnie ten cały nawias i uprościć licznik:
, który przed chwilą stworzyliśmy korzystając ze wzoru skróconego mnożenia. Dzięki temu będziemy mogli wyciągnąć przed nawias właśnie ten cały nawias i uprościć licznik: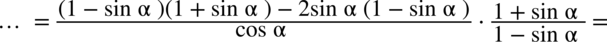
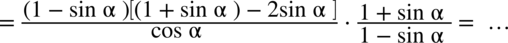


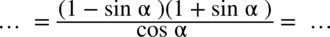
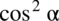 :
: 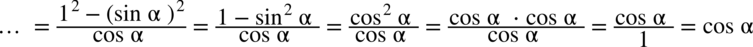
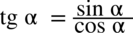 oraz
oraz  :
: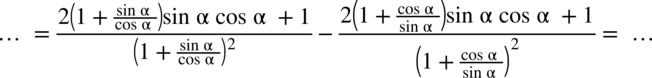
 :
: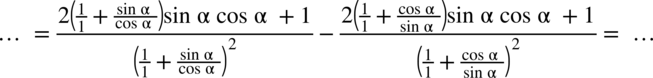
 , a dla drugiego
, a dla drugiego 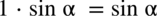 :
: 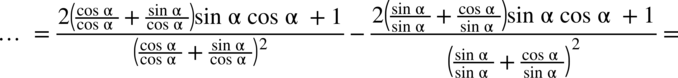
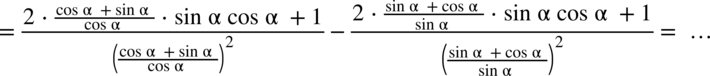
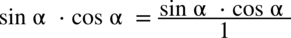 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie), natomiast w mianownikach skorzystamy z własności potęg
nie ulega zmianie), natomiast w mianownikach skorzystamy z własności potęg 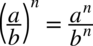 :
: 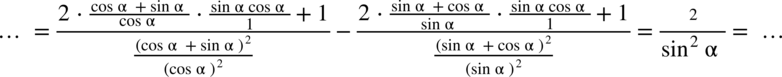

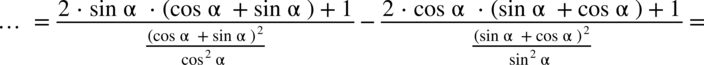
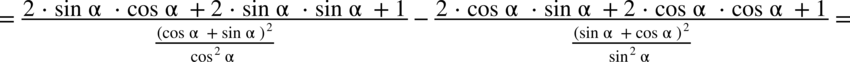
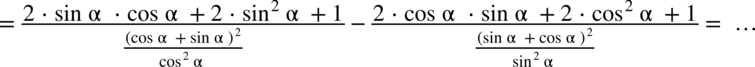
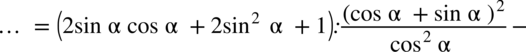
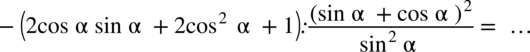



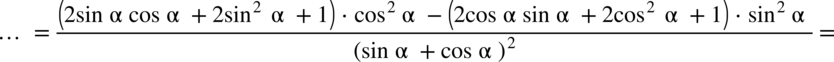
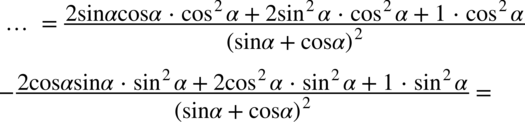
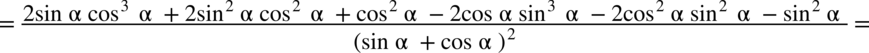
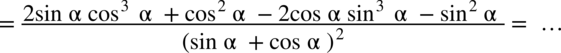
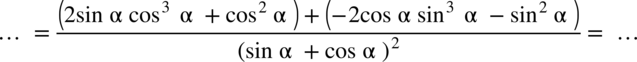
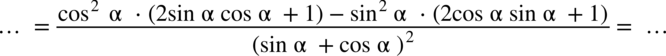
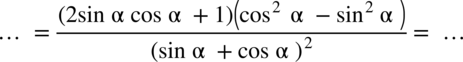
 :
: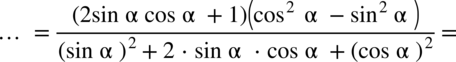
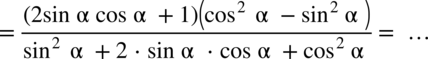
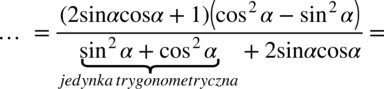

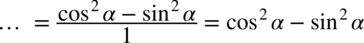
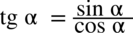 oraz
oraz  :
: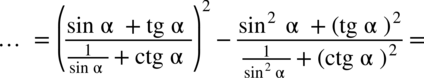
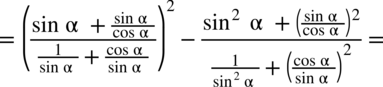
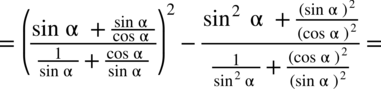
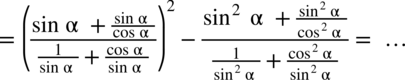
 oraz
oraz 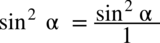 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
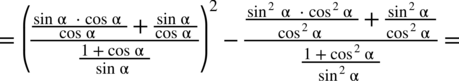
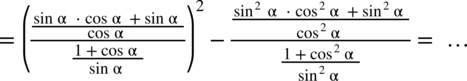
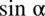 oraz
oraz 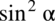 :
: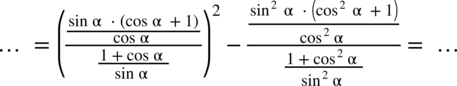
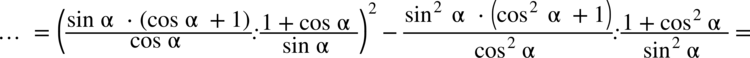
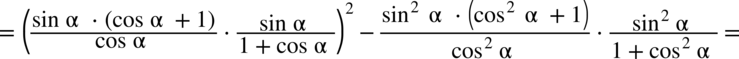
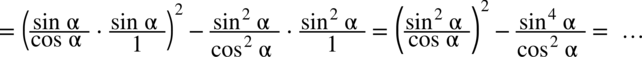
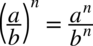 :
: