
W losowo wybranej próbie 200 studentów pewnej uczelni 70 osób wydaje miesięcznie na gazety i czasopisma ponad 10 zł. Jaka powinna być liczebność próby, aby oszacować odsetek studentów wydających miesięcznie na gazety i czasopisma ponad 10 zł z maksymalnym błędem nieprzekraczającym 2%, przy współczynniku ufności 0,98?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
“ Jaka powinna być liczebność próby, aby oszacować odsetek studentów wydających miesięcznie na gazety i czasopisma ponad 10 zł z maksymalnym błędem nieprzekraczającym 2%, przy współczynniku ufności 0,98? ”
Występują tu zwroty: jaka powinna być liczebność próby ... , z maksymalnym błędem ... . Pojawia się również wyrażenie współczynnik ufności . Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Czytamy zdanie po zdaniu.
W losowo wybranej próbie 200 studentów pewnej uczelni 70 osób wydaje miesięcznie na gazety i czasopisma ponad 10 zł.
Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej studentów tzw. pilotażowej, którą oznaczamy
 . Ponadto dowiadujemy się, że 70 osób z 200 wylosowanych studentów wydaje miesięcznie na gazety i czasopisma ponad 10 zł. Jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Ponadto dowiadujemy się, że 70 osób z 200 wylosowanych studentów wydaje miesięcznie na gazety i czasopisma ponad 10 zł. Jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
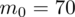 . Dzięki tym danym możemy obliczyć procent, a więc wskaźnik struktury z próby pilotażowej
. Dzięki tym danym możemy obliczyć procent, a więc wskaźnik struktury z próby pilotażowej
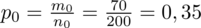 .
.
“ Jaka powinna być liczebność próby, aby oszacować odsetek studentów wydających miesięcznie na gazety i czasopisma ponad 10 zł z maksymalnym błędem nieprzekraczającym 2%, przy współczynniku ufności 0,98? ”
Szukamy liczebności próby właściwej, którą oznaczamy literą
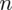 . Maksymalny błąd szacunku wynosi
. Maksymalny błąd szacunku wynosi
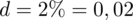 . Współczynnik ufności wynosi
. Współczynnik ufności wynosi
 . Od razu wyznaczamy
. Od razu wyznaczamy
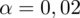 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA
studenci pewnej uczelni
|
PRÓBA
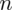 wybranych studentów
wybranych studentów
|
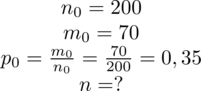
|
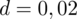
 - współczynnik ufności,
- współczynnik ufności,
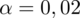
3. WYBÓR ODPOWIEDNIEGO WZORU.
Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy
 jest znana. Stwierdzamy, że
jest znana. Stwierdzamy, że
 nie jest znana
, zatem wykluczamy model I.
Mamy próbę pilotażowej o konkretnej liczebności
, ale niemożliwe jest wyliczenie wariancji
nie jest znana
, zatem wykluczamy model I.
Mamy próbę pilotażowej o konkretnej liczebności
, ale niemożliwe jest wyliczenie wariancji
 , wobec tego odrzucamy również modele II i III. W zamian mogliśmy obliczyć
spodziewany wskaźnik struktury
, wobec tego odrzucamy również modele II i III. W zamian mogliśmy obliczyć
spodziewany wskaźnik struktury
 z próby pilotażowej
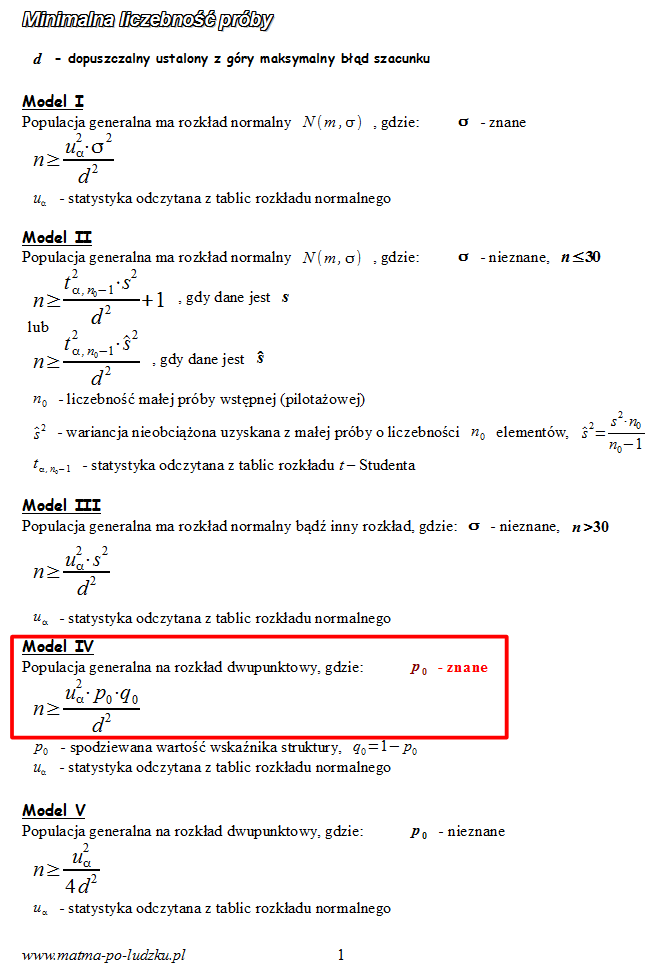
, zatem wybieramy
model IV
.
z próby pilotażowej
, zatem wybieramy
model IV
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
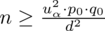 konkretnymi liczbami. Zgodnie ze wzorem
konkretnymi liczbami. Zgodnie ze wzorem
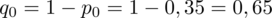 .
.
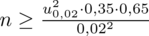
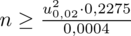
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka
u
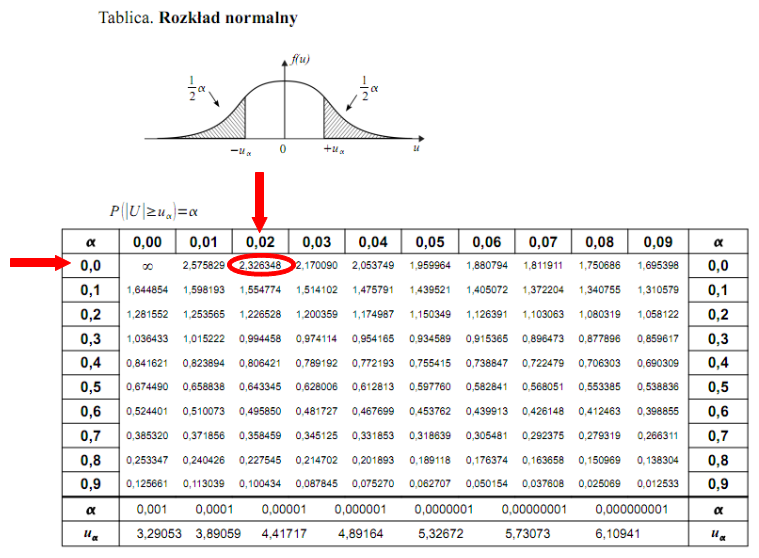
, zatem skorzystamy z tablic rozkładu normalnego:
http://matma-po-ludzku.pl/materialy/statystyka/wzory/rnormalny.pdf
. Zapis
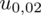 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
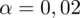 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
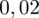 sumujemy
sumujemy
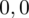 i
i
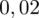 czyli
czyli
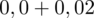 .
.
Wracamy do obliczeń i podstawiamy
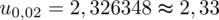 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
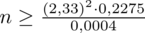
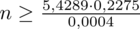
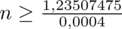
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
 , czyli ZAWSZE zaokrąglając w górę otrzymujemy
, czyli ZAWSZE zaokrąglając w górę otrzymujemy
 .
.
Interpretacja brzmi następująco: Aby oszacować odsetek studentów wydających miesięcznie na gazety i czasopisma ponad 10 zł z ufnością 0,98 należy wylosować do próby 3088 studentów.