Na podstawie wyników badania ankietowego przeprowadzonego w grupie 500 studentów stwierdzono, że 100 spośród nich nie ma kłopotów finansowych. Ilu studentów należałoby wylosować do próby w celu oszacowania odsetka studentów mających kłopoty finansowe, aby przy niezmienionej wiarygodności oszacowania zwiększyć dwukrotnie jego dokładność? Przyjmij poziom ufności 0,95.

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Ilu studentów należałoby wylosować do próby w celu oszacowania odsetka studentów mających kłopoty finansowe, aby przy niezmienionej wiarygodności oszacowania zwiększyć dwukrotnie jego dokładność? ”

Występuje tu zwrot: ilu studentów należałoby wylosować do próby ... . Co prawda nie pojawia się bezpośrednio wyrażenie maksymalny dopuszczalny błąd szacunku, ale można odnaleźć stwierdzenie bezpośrednio wskazujące na ten parametr: przy niezmienionej wiarygodności oszacowania zwiększyć dwukrotnie jego dokładność ... . W kolejnym zdaniu pojawia się również wyrażenie poziom ufności . Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Na podstawie wyników badania ankietowego przeprowadzonego w grupie 500 studentów stwierdzono, że 100 spośród nich nie ma kłopotów finansowych.

Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej studentów tzw. pilotażowej, której liczebność oznaczamy . Ponadto dowiadujemy się, że 100 studentów z 500 wylosowanych nie ma kłopotów finansowych, ale uwaga, w następnym zdaniu jest mowa o studentach mających kłopoty finansowe, a więc to oni stanowią ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem . Dzięki tym danym możemy obliczyć procent, a więc wskaźnik struktury z próby pilotażowej .

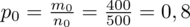“ Ilu studentów należałoby wylosować do próby w celu oszacowania odsetka studentów mających kłopoty finansowe, aby przy niezmienionej wiarygodności oszacowania zwiększyć dwukrotnie jego dokładność? ”

Szukamy liczebności próby właściwej, którą oznaczamy literą 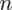. Dokładność oszacowania, a więc maksymalny błąd szacunku 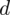nie jest jeszcze konkretną liczbą. Wiemy na razie tylko, że ma być on dwa razy lepszy od precyzji w próbie 500-elementowej, bo tylko taką mamy do porównania. Wrócimy do tego problemu w dalszych obliczeniach.

Przyjmij poziom ufności 0,95.

Współczynnik ufności wynosi . Od razu wyznaczamy .

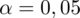Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA studenci	PRÓBA 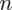wybranych studentów

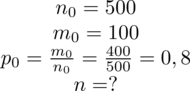
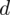(dwa razy lepsze niż w przypadku próby 500-elementowej)

- współczynnik ufności,

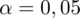
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Mamy próbę pilotażowej o konkretnej liczebności , ale niemożliwe jest wyliczenie wariancji , wobec tego odrzucamy również modele II i III. W zamian mogliśmy obliczyć spodziewany wskaźnik struktury z próby pilotażowej , zatem wybieramy model IV .

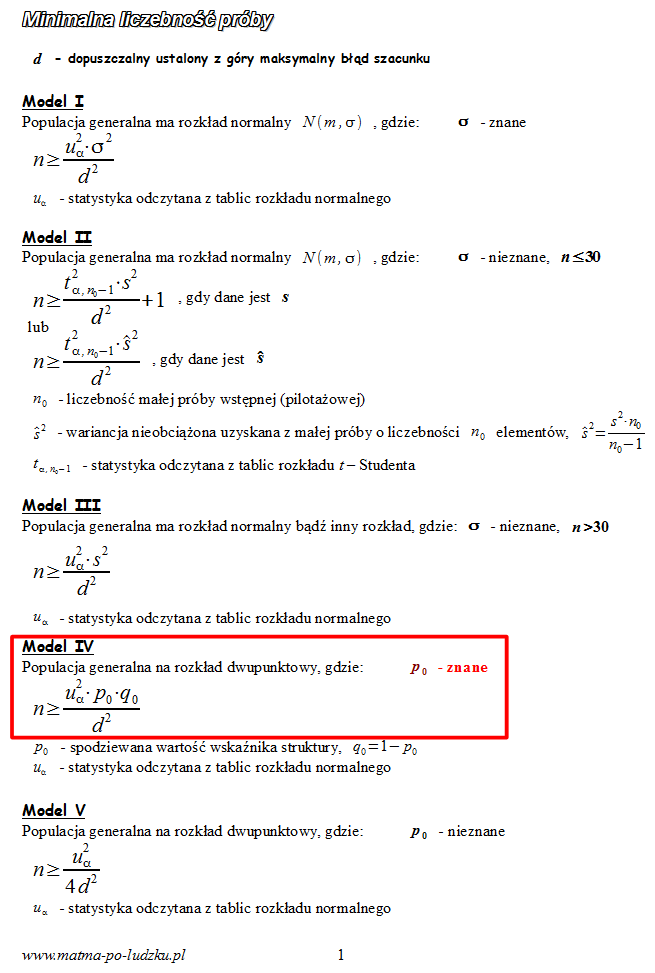
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 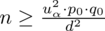konkretnymi liczbami. Zgodnie ze wzorem .

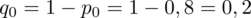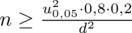
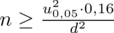
I tu pojawia się problem, ponieważ w zadaniu nie ma konkretnej wartości 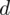, czyli maksymalnego błędu szacunku. Jednak mamy w treści zadania informację, że błąd ten ma być dwa razy lepszy od precyzji w próbie 500-elementowej. Ale jaki jest wzór na błąd w próbie?

Aby odpowiedzieć na to pytanie chwilowo wrócimy do estymacji przedziałowej i wybierzemy model, który pasuje do naszych danych (wzory na minimalną liczebność próby zostały wyprowadzone właśnie z modeli estymacji przedziałowej). Przypominam, że czwarty model dotyczący minimalnej liczebności próby jest ściśle związany z szacowaniem wskaźnika struktury w populacji. Wobec tego bierzemy pod uwagę modele estymacji wskaźnika struktury . Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby , gdzie jak pamiętamy w minimalnej liczebności próby (tylko!) oznaczamy go symbolem .

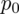No dobrze, wzór wybrany, ale nadal nie ma śladu 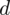. Przypominam, że we wzorze na dany model wartość 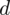to wielkość odjęta i dodana od :

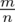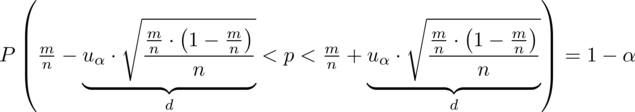
czyli

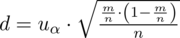
Wracamy do danych i uzupełniamy wzór:

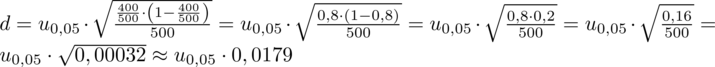
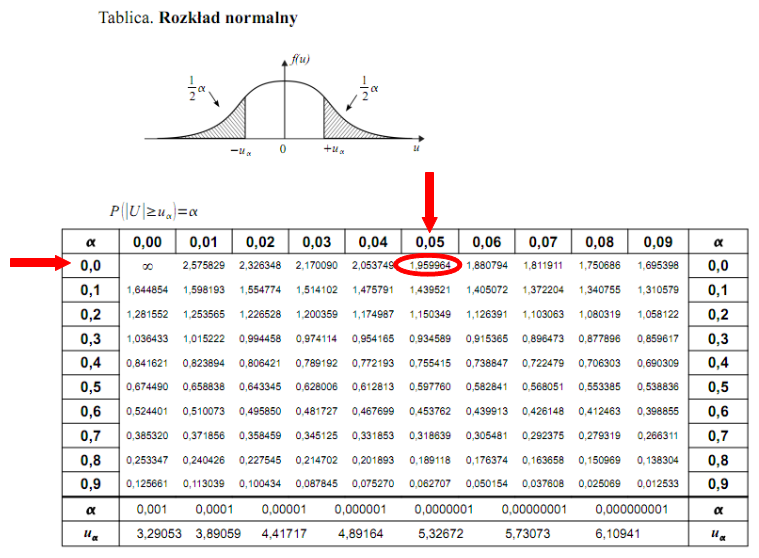
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u , zatem skorzystamy z tablic rozkładu normalnego: http://matma-po-ludzku.pl/materialy/statystyka/wzory/rnormalny.pdf . Zapis 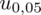oznacza konieczność odnalezienia statystyki dla 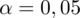. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. 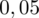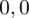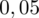W przypadku sumujemy i czyli .

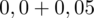Wracamy do obliczeń i podstawiamy do formuły 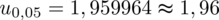(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):

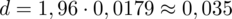
Właśnie obliczyliśmy błąd szacunku 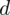dla próby 500-elementowej, ale w tym zadaniu interesuje nas dwa razy lepsze 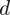niż w przypadku próby 500-elementowej. W tym momencie należy pomyśleć logicznie i absolutnie nie będziemy mnożyć przez 2! Precyzja oszacowania jest lepsza wtedy, gdy błąd szacunku jest niższy, a więc w naszym przypadku musimy dzielić na 2 wartość 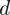. Zatem żądany błąd szacunku do określenia minimalnej liczebności próby .

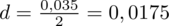Teraz możemy wrócić do obliczeń na minimalną liczebność próby i otrzymujemy:

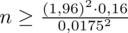
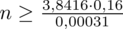
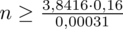
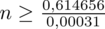
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 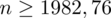, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

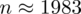Interpretacja brzmi następująco: Aby przy niezmienionej wiarygodności oszacowania zwiększyć dwukrotnie jego dokładność ufnością 0,95 należy wylosować do próby 1983 studentów.