Wylosowano 26 studentów uczelni sportowej, by oszacować przeciętny wynik skoku wzwyż ogółu uczelni sportowych. W próbie stwierdzono odchylenie standardowe 5 cm. Przyjmując do wnioskowania 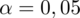wskaż minimalną liczebność próby dającą możliwość oszacowania z precyzją dwa razy lepszą niż przy próbie 26 osobowej:

a) 101 b) 90 c) 159 d) 841

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Przyjmując do wnioskowania 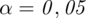wskaż minimalną liczebność próby dającą możliwość oszacowania z precyzją dwa razy lepszą niż przy próbie 26 osobowej ”

Występują tu zwroty: wskaż minimalną liczebność próby , możliwość oszacowania z precyzją... (inaczej z błędem szacunku). Co prawda nie ma wyrażenia: poziom ufności, ale mamy już gotową wartość 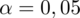. Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Wylosowano 26 studentów uczelni sportowej, by oszacować przeciętny wynik skoku wzwyż ogółu uczelni sportowych.

Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej (pilotażowej), którą oznaczamy studentów.

W próbie stwierdzono odchylenie standardowe 5 cm.

Dowiadujemy się, że odchylenie standardowe w próbie wstępnej wynosi cm. Oczywiście użyto symbolu odchylenia dla próby.

“ Przyjmując do wnioskowania 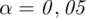wskaż minimalną liczebność próby dającą możliwość oszacowania z precyzją dwa razy lepszą niż przy próbie 26 osobowej ”

Podano tu nie współczynnik ufności, ale już gotową 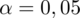, więc nie musimy jej obliczać. Szukamy liczebności próby właściwej, którą oznaczamy literą 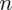. Precyzja oszacowania, a więc maksymalny błąd szacunku 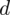nie jest jeszcze konkretną liczbą. Wiemy na razie tylko, że ma być on dwa razy lepszy od precyzji w próbie 26 osobowej. Wrócimy do tego problemu w dalszych obliczeniach.

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA studenci uczelni sportowych	PRÓBA 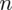wybranych studentów

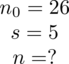
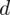(dwa razy lepsze niż w przypadku próby 26 osobowej)

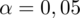
3. WYBÓR ODPOWIEDNIEGO WZORU.

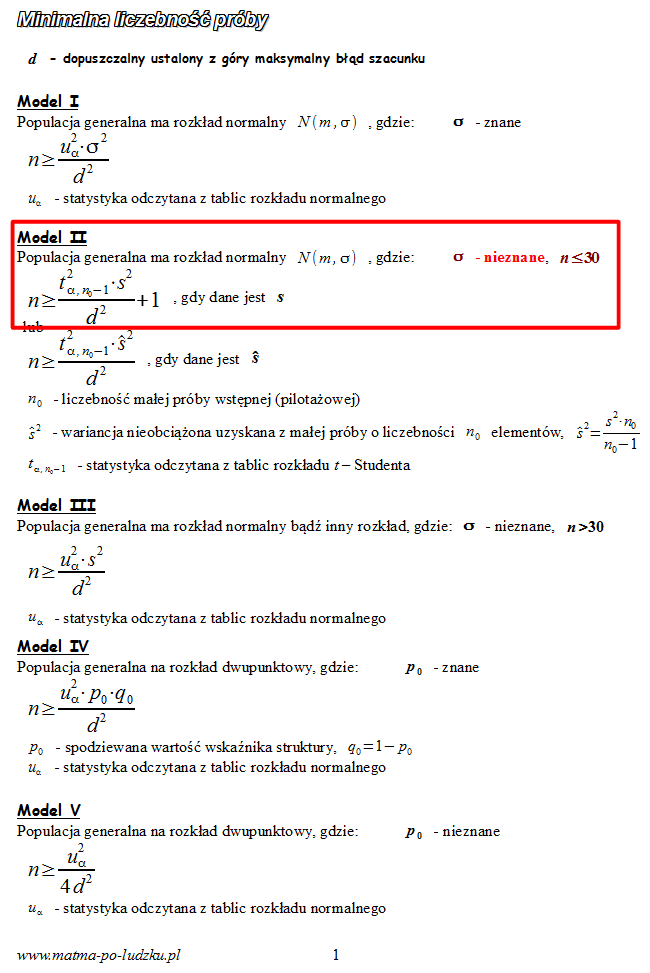
Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ) i znane jest - wobec tego wybieramy model II . Wybieramy wersję bez daszka, oczywiście można wybrać wersję z daszkiem, ale wypadałoby przeliczyć na .

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 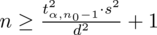konkretnymi liczbami.

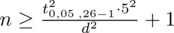
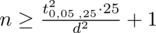
I tu pojawia się problem, ponieważ w zadaniu nie ma konkretnej wartości 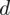, czyli maksymalnego błędu szacunku. Jednak mamy w treści zadania informację, że błąd ten ma być dwa razy lepszy od precyzji w próbie 26 osobowej. Ale jaki jest wzór na błąd w tejże próbie?

Aby odpowiedzieć na to pytanie chwilowo wrócimy do estymacji przedziałowej i wybierzemy model, który pasuje do naszych danych (wzory na minimalną liczebność próby zostały wyprowadzone właśnie z modeli estymacji przedziałowej). Przypominam, że pierwsze trzy modele dotyczące minimalnej liczebności próby (w ty nasz model II) są ściśle związane z szacowaniem średniej w populacji. Wobec tego bierzemy pod uwagę modele estymacji średniej . Potwierdzenie znajdujemy w zdaniu:

Wylosowano 26 studentów uczelni sportowej, by oszacować przeciętny wynik skoku wzwyż ogółu uczelni sportowych.

Mamy do wyboru trzy modele. Sprawdzamy: nie jest znana oraz liczebność jest mniejsza niż 30 ( ), zatem wybieramy model II . W danych mamy , więc interesuje nas wersja wzoru bez daszka.

No dobrze, wzór wybrany, ale nadal nie ma śladu 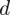. Przypominam, że we wzorze na dany model wartość 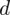to wielkość odjęta i dodana do średniej :

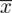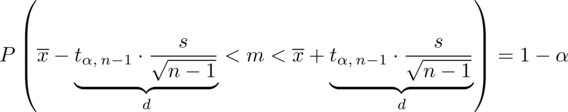
Zatem .

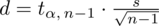Wracamy do danych i uzupełniamy wzór:

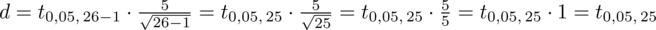
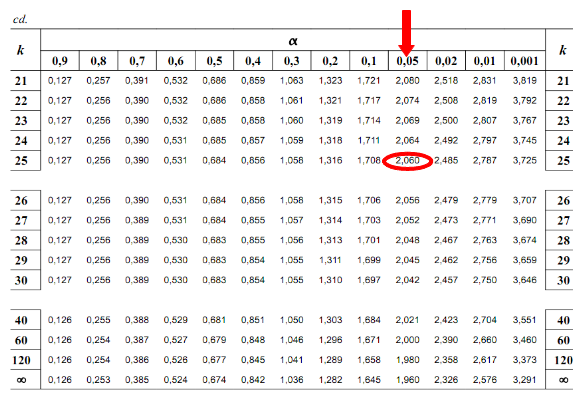
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 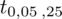oznacza konieczność odnalezienia statystyki dla 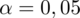i 25 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

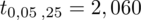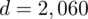cm

Właśnie obliczyliśmy błąd szacunku 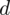dla próby 26-osobowej, ale w tym zadaniu interesuje nas dwa razy lepsze 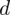niż w przypadku próby 26 osobowej. I teraz należy pomyśleć logicznie i absolutnie nie będziemy mnożyć przez 2! Precyzja oszacowania jest lepsza wtedy, gdy błąd szacunku jest niższy, a więc w naszym przypadku musimy dzielić na 2 wartość 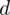. Zatem żądany błąd szacunku do określenia minimalnej liczebności próby .

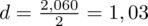Teraz możemy wrócić do obliczeń na minimalną liczebność próby i otrzymujemy:

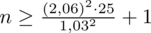
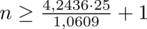
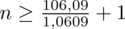
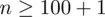
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: , czyli otrzymujemy 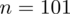(nie ma potrzeby zaokrąglania, bo liczba jest całkowita).

Interpretacja brzmi następująco: Aby oszacować przeciętny wynik skoku wzwyż ogółu uczelni sportowych z ufnością 0,95 (bo 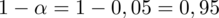), do próby należy wylosować 101 studentów, czyli odpowiedź A.