W oparciu o próbkę o liczebności 13 osób stwierdzono, że zawartość pewnego składnika odżywczego w konserwach oferowanych w handlu wynosi średnio 70 ze współczynnikiem zmienności 16%. Ile puszek konserw należy wylosować, by szacować poziom składnika przy ?

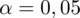a) 13 b) 68 c) 304 d) 149 e) inna liczebność, jaka? ...

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Ile puszek konserw należy wylosować, by szacować poziom składnika przy ? ”

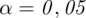Występuje tu zwrot: ile puszek konserw należy wylosować ... . Podano również gotową wartość 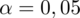. Nie ma wszystkich słów-kluczy, ale mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby ze względu na podane wyrażenie (ile należy wylosować do próby), które jest najważniejsze w odróżnianiu tego typu zadań.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

“ W oparciu o próbkę o liczebności 13 osób stwierdzono, że zawartość pewnego składnika odżywczego w konserwach oferowanych w handlu wynosi średnio 70 ze współczynnikiem zmienności 16% .”

Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej (pilotażowej), którą oznaczamy . Uzyskujemy również informację, że zawartość składnika w puszce konserwy w próbie wstępnej wynosi średnio 70, a więc jest to średnia, którą oznaczymy .

Podano również współczynnik zmienności dla próby, który zapisuje się jako 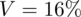. Od razu rozszyfrujmy czym jest ten parametr. Współczynnik zmienności to iloraz odchylenia standardowego i średniej (podaje się go najczęściej w procentach), czyli 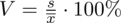. Podstawiając średnią i wartość współczynnika możemy wyznaczyć wartość odchylenia standardowego w próbie wstępnej:

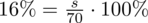
Następnie stosując najzwyklejsze przekształcenia matematyczne wyznaczmy . Na początku można pozbyć się np. procentów, więc dzielimy przez :

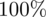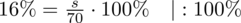
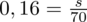
Teraz wystarczy pomnożyć obie strony przez 70 i uzyskujemy :

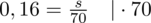
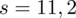
“ Ile puszek konserw należy wylosować, by szacować poziom składnika przy ? ”

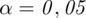Szukamy liczebności próby, którą oznaczamy literą 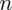. Tym razem podano gotową wyznaczoną 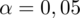, a nie współczynnik ufności.

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA konserwy oferowane w handlu	PRÓBA wybranych puszek

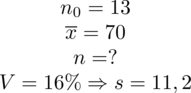
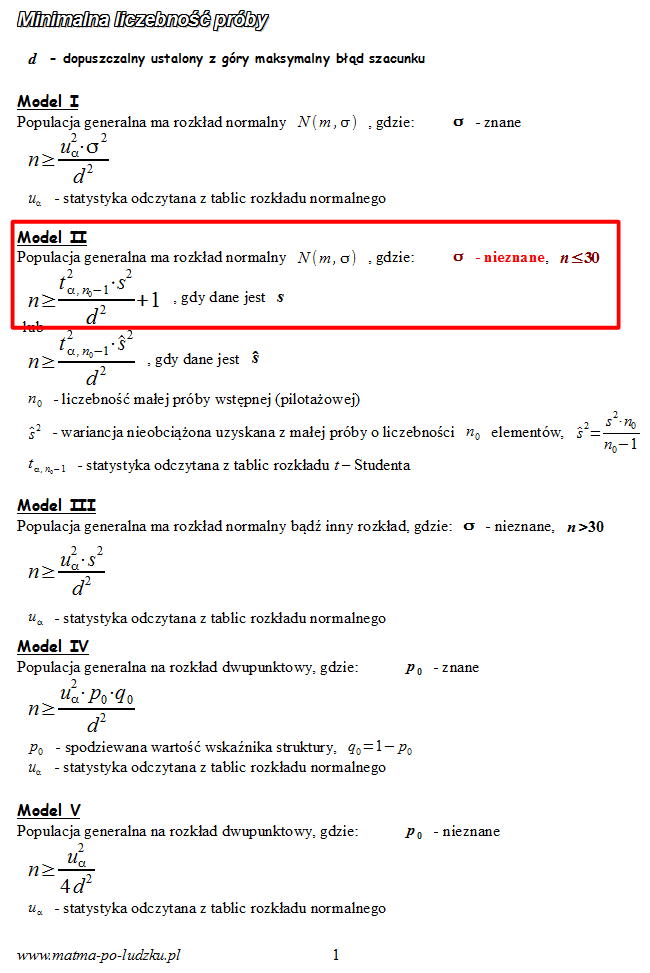
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ) i znane jest - wobec tego wybieramy model II . Wybieramy wersję bez daszka, oczywiście można wybrać wersję z daszkiem, ale wypadałoby przeliczyć na .

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 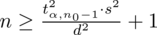konkretnymi liczbami.

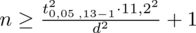
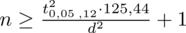
I tu pojawia się problem, ponieważ w zadaniu nie ma słowa o wartości 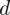, czyli o maksymalnym błędzie szacunku.

Od razu ominę dalsze obliczenia w tym specyficznym wypadku i podam wynik. Warto pamiętać, że nie mając jakichkolwiek założeń co do 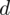, minimalna liczebność próby zawsze wyjdzie równa liczebności próby pilotażowej (w naszym przypadku ).

Mogłabym właściwie zakończyć na poprzednim stwierdzeniu, ale z racji tego, że w kolejnych dwóch zadaniach wartość maksymalnego błędu szacunku 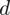będzie potrzebna i nie otrzymamy tak kuriozalnego przypadku, pokażę jak obliczyć wartość 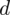, gdy nie ma go bezpośrednio podanego w treści zadania.

Na początku wrócimy do estymacji przedziałowej i wybierzemy model, który pasuje do naszych danych (wzory na minimalną liczebność próby zostały wyprowadzone właśnie z modeli estymacji przedziałowej). Przypominam, że pierwsze trzy modele dotyczące minimalnej liczebności próby (w tym nasz model II) są ściśle związane z szacowaniem średniej w populacji. Wobec tego bierzemy pod uwagę modele estymacji średniej . Mamy do wyboru trzy modele. Sprawdzamy: nie jest znana oraz liczebność jest mniejsza niż 30 ( ), zatem wybieramy model II . W danych mamy , więc interesuje nas wersja wzoru bez daszka.

No dobrze, wzór wybrany, ale nadal nie ma śladu 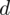. Przypominam, że we wzorze na dany model wartość 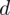to wielkość odjęta i dodana do średniej :

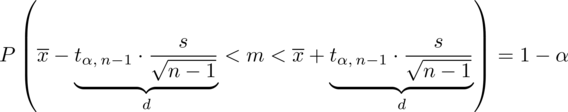
Zatem .

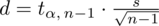Wracamy do danych i uzupełniamy wzór:

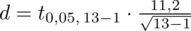
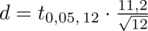
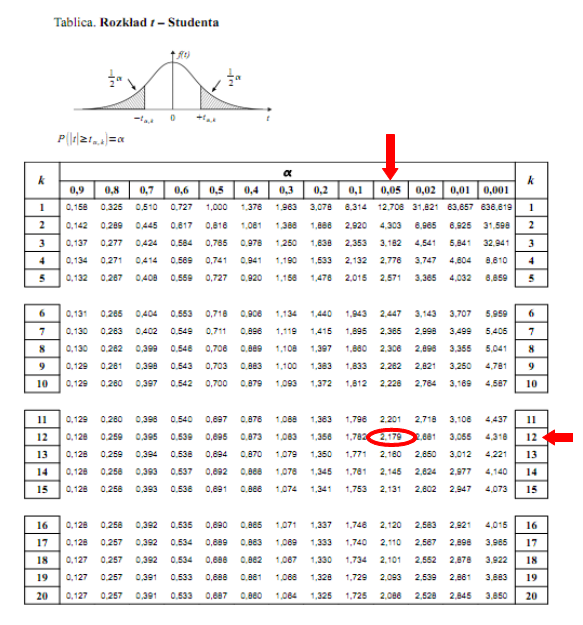
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 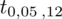oznacza konieczność odnalezienia statystyki dla 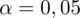i 12 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

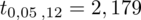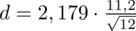
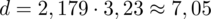
Teraz możemy wrócić do obliczeń na minimalną liczebność próby i otrzymujemy:

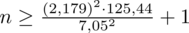
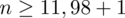
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 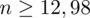, czyli ZAWSZE zaokrąglając w górę otrzymujemy 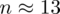(gdyby nie zaokrąglać wyników w pośrednich obliczeniach, to dokładnie otrzymamy 13).

Interpretacja brzmi następująco: Aby oszacować przeciętną zawartość pewnego składnika odżywczego w konserwach oferowanych w handlu z ufnością 0,95 (bo 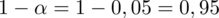), do próby należy wylosować 13 puszek, czyli odpowiedź A. Można się pokusić o stwierdzenie, że jest to nieokreślona liczba puszek, ponieważ maksymalny błąd szacunku nie został określony, a więc odpowiedź E.