Jaką liczbę tynkarzy pewnego kombinatu budowlanego należy pobrać do próby, aby przy współczynniku ufności 0,98 oszacować średnią wydajność ich pracy (w m ² /h) z błędem nie przekraczającym 10%, jeżeli dla 20 losowo wybranych tynkarzy średnia wydajność wynosiła 5, zaś nieobciążona wariancja wynosi 0,8836?

a) 23 b) 24 c) 540 d) 22 e) żadna odpowiedź nie jest poprawna

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na:

“ Jaką liczbę tynkarzy pewnego kombinatu budowlanego należy pobrać do próby, aby przy współczynniku ufności 0,98 oszacować średnią wydajność ich pracy (w m ² /h) z błędem nie przekraczającym 10%, jeżeli dla 20 losowo wybranych tynkarzy średnia wydajność wynosiła 5, zaś nieobciążona wariancja wynosi 0,8836? ”

Występują tu zwroty: jaką liczbę tynkarzy (...) należy pobrać do próby , przy współczynniku ufności.... oraz z błędem nie przekraczającym... .Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zadanie i wyławiamy dane liczbowe.

“ Jaką liczbę tynkarzy pewnego kombinatu budowlanego należy pobrać do próby, aby przy współczynniku ufności 0,98 oszacować średnią wydajność ich pracy (w m ² /h) z błędem nie przekraczającym 10%, jeżeli dla 20 losowo wybranych tynkarzy średnia wydajność wynosiła 5, zaś nieobciążona wariancja wynosi 0,8836? ”

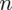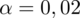Szukamy liczebności próby tynkarzy, którą oznaczamy literą . Podano również współczynnik ufności, a więc . Od razu wyznaczamy . Znamy również maksymalny błąd szacunku, który wynosi 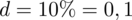. Następnie dowiadujemy się, że liczebność próby tynkarzy wynosi 20. Oczywiście wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej tzw. pilotażowej, którą oznaczamy . Uzyskujemy również informację, że średnia wydajność w tej próbie wynosi 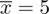m ² /h oraz nieobciążona wariancja dla tejże próby (nieobciążona - tzw. z daszkiem) wynosi 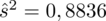. Oczywiście użyliśmy oznaczeń dla próby.

Dane liczbowe zostały już przeanalizowane, ale wrócimy na chwilę do maksymalnego błędu szacunku 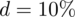. Trzeba pamiętać, że musi on być podany w tych samych jednostkach co inne parametry z próby - w naszym przypadku jednostką jest m ² /h. Nie może być tak, że na przykład średnia czy odchylenie z próby jest podane w m ² /h, a błąd szacunku w procentach lub ułamku. Co zatem zrobić w takim przypadku? Przyjrzyjmy się jeszcze raz treści zadania i znajdźmy jaki parametr ma być szacowany przy szukanej przez nas minimalnej liczebności próby:

“ Jaką liczbę tynkarzy pewnego kombinatu budowlanego należy pobrać do próby, aby przy współczynniku ufności 0,98 oszacować średnią wydajność ich pracy (w m ² /h) z błędem nie przekraczającym 10%, jeżeli dla 20 losowo wybranych tynkarzy średnia wydajność wynosiła 5, zaś nieobciążona wariancja wynosi 0,8836? ”

Szacujemy średnią dla populacji wszystkich tynkarzy i to dla niej szukamy błędu szacunku. Problem w tym, że średniej dla wszystkich tynkarzy nie znamy. Wobec tego przyjmuje się, że ten 10% błąd obliczymy ze średniej z próby pilotażowej, a więc 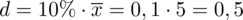m ² /h.

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA tynkarze pewnego kombinatu budowlanego	PRÓBA 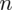wybranych tynkarzy

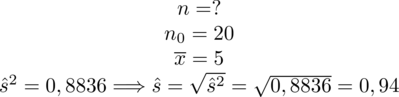
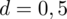
- współczynnik ufności,

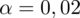
3. WYBÓR ODPOWIEDNIEGO WZORU.

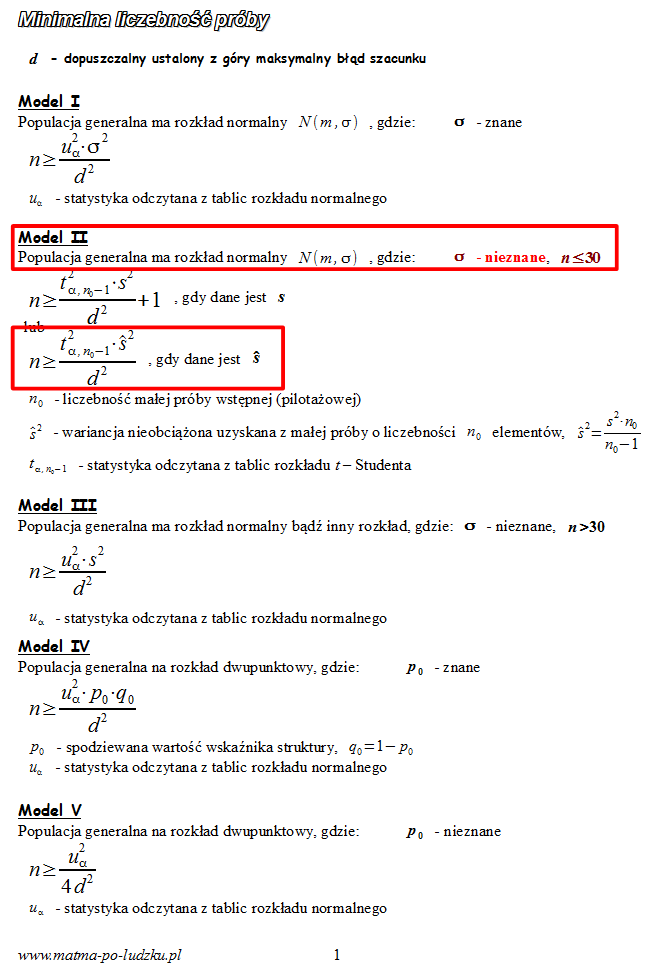
Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ) i znane jest - wobec tego wybieramy model II . Wybieramy wersję wzoru z (z daszkiem).

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 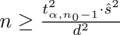konkretnymi liczbami. Pamiętajmy, że już mamy , więc nie podnosimy wartości 0,8836 do kwadratu.

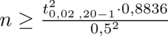
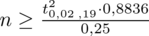
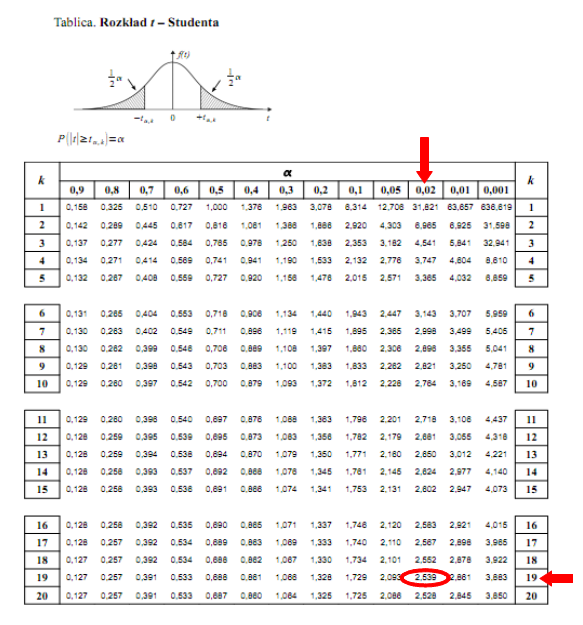
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 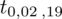oznacza konieczność odnalezienia statystyki dla 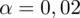i 19 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

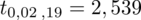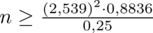
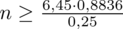
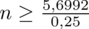
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 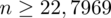, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

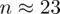Interpretacja brzmi następująco: Aby oszacować średni średnią wydajność pracy tynkarzy z ufnością 0,98 do próby należy wylosować 23 tynkarzy. Wybieramy odpowiedź A.