J aką liczbę drzew z lasów sosnowych należy wylosować do próby, aby przy współczynniku ufności 0,99 oszacować przeciętną wysokość drzewa w lesie sosnowym? Wariancja wysokości drzew obliczona z pilotażowej 10-elementowej próby wyniosła 25 cm ² . Zakładamy maksymalny błąd szacunku równy 5 cm.

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdania:

“ Jaką liczbę drzew z lasów sosnowych należy wylosować do próby, aby przy współczynniku ufności 0,99 oszacować przeciętną wysokość drzewa w lesie sosnowym? ”

Zakładamy maksymalny błąd szacunku równy 5 cm.

Występują tu zwroty: jaką liczbę drzew (...) należy wylosować do próby... , maksymalny błąd szacunku... . Odnajdujemy również wyrażenie: współczynnik ufności . Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

“ Jaką liczbę drzew z lasów sosnowych należy wylosować do próby, aby przy współczynniku ufności 0,99 oszacować przeciętną wysokość drzewa w lesie sosnowym? ”

Szukamy liczebności próby, którą oznaczamy literą 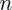. Podano również współczynnik ufności, a więc . Od razu wyznaczamy .

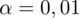Wariancja wysokości drzew obliczona z pilotażowej 10-elementowej próby wyniosła 25 cm ² .

Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej, którą oznaczamy . Uzyskujemy również informację, że wariancja w próbie wstępnej wynosi cm ² . Oczywiście użyto oznaczeń parametrów dla próby. Wariancja wysokości drzew jest określona w dziwnej jednostce - cm ² , ale w przypadku wariancji (jednostka podniesiona do kwadratu) nie jest to nic nadzwyczajnego i nie należy na to zwracać większej uwagi. Przyjęło się zresztą, że samej wariancji się nie interpretuje, ale już odchylenie standardowe, które jest pierwiastkiem z wariacji - jak najbardziej.

Zakładamy maksymalny błąd szacunku równy 5 cm.

Maksymalny dopuszczalny błąd szacunku wynosi cm.

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA drzewa z lasów sosnowych	PRÓBA 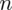wybranych drzew

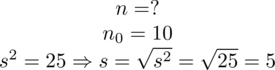
- współczynnik ufności,

3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykluczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ) i znane jest - wobec tego wybieramy model II . Wybieramy wersję bez daszka, oczywiście można wybrać wersję z daszkiem, ale wypadałoby przeliczyć na .

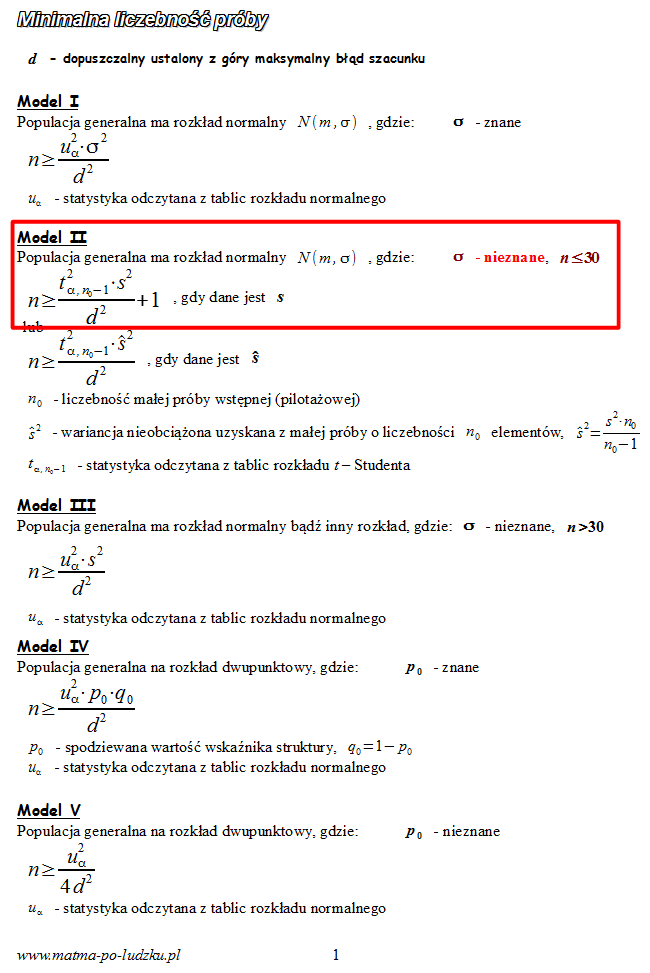
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 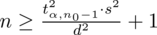konkretnymi liczbami. Pamiętajmy, aby nie podnosić do kwadratu , bo ta operacja została już wykonana.

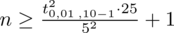
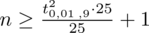
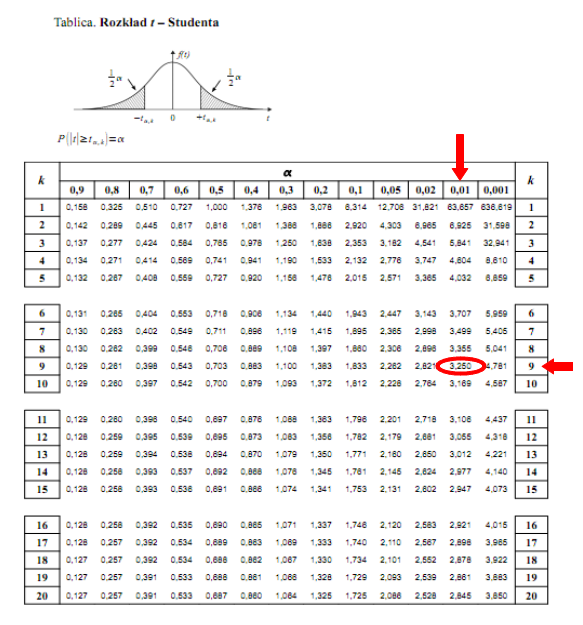
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 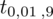oznacza konieczność odnalezienia statystyki dla 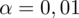i 9 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

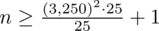
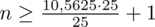
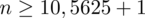
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: , czyli ZAWSZE zaokrąglając w górę otrzymujemy .

Interpretacja brzmi następująco: Aby oszacować przeciętną wysokość drzewa w lesie sosnowym z ufnością 0,99, do próby należy wylosować 12 drzew (albo dolosować do próby pilotażowej 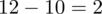drzewa).