Firma marketingowa Onlimany zamierza zbadać dochody ludności gminy Pępowo. Na podstawie dziesięcioelementowej próby wstępnej stwierdzono m.in., że odchylenie standardowe dochodu na jednego mieszkańca wynosi 209,4 zł. Oszacować niezbędną wielkość próby dla maksymalnego dopuszczalnego błędu szacunku 10 zł, przy współczynniku ufności 0,95.

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Oszacować niezbędną wielkość próby dla maksymalnego dopuszczalnego błędu szacunku 10 zł, przy współczynniku ufności 0,95. ”

Występują tu zwroty: oszacować niezbędną wielkość próby... , dla maksymalnego dopuszczlnego błędu szacunku.... Odnajdujemy również wyrażenie: współczynnik ufności . Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Firma marketingowa Onlimany zamierza zbadać dochody ludności gminy Pępowo.

W tym zdaniu nie ma żadnych danych liczbowych, więc je pomijamy.

Na podstawie dziesięcioelementowej próby wstępnej stwierdzono m.in., że odchylenie standardowe dochodu na jednego mieszkańca wynosi 209,4 zł.

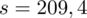Wydaje się dziwne, że w zadaniu, którego istotą jest znalezienie liczebności próby podaje się właśnie to, czego szukamy - a więc liczebność próby. Nie ma powodu do niepokoju - jest to liczebność próby wstępnej, którą oznaczamy . Uzyskujemy również informację, że odchylenie standardowe w próbie wstępnej wynosi zł. Oczywiście użyto oznaczeń parametrów dla próby.

“ Oszacować niezbędną wielkość próby dla maksymalnego dopuszczalnego błędu szacunku 10 zł, przy współczynniku ufności 0,95. ”

Szukamy liczebności próby właściwej, którą oznaczamy literą 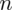. Z kolei maksymalny dopuszczalny błąd szacunku wynosi zł. Podano również współczynnik ufności, a więc . Od razu wyznaczamy .

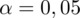Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA ludność gminy Pępowo	PRÓBA 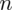wybranych mieszkańców gminy

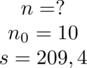
- współczynnik ufności,

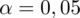
3. WYBÓR ODPOWIEDNIEGO WZORU.

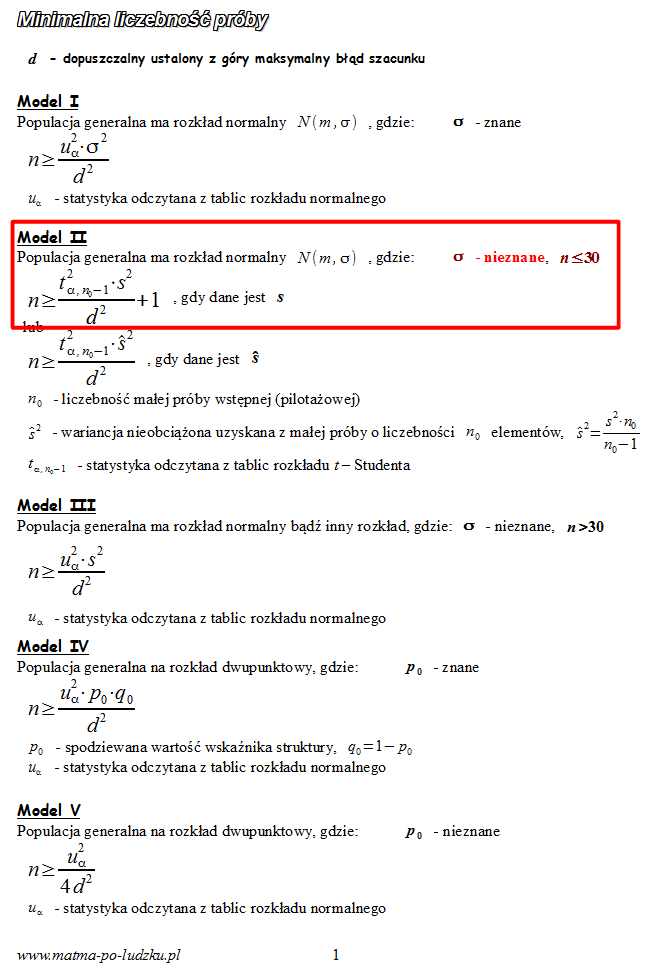
Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że nie jest znana , zatem wykulczamy model I. Ponadto wiemy, że mamy do czynienia z próbą pilotażową, której liczebność jest mniejsza niż 30 ( ) i znane jest - wobec tego wybieramy model II . Wybieramy wersję bez daszka, oczywiście można wybrać wersję z daszkiem, ale wypadałoby przeliczyć na .

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 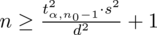konkretnymi liczbami.

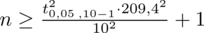
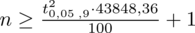
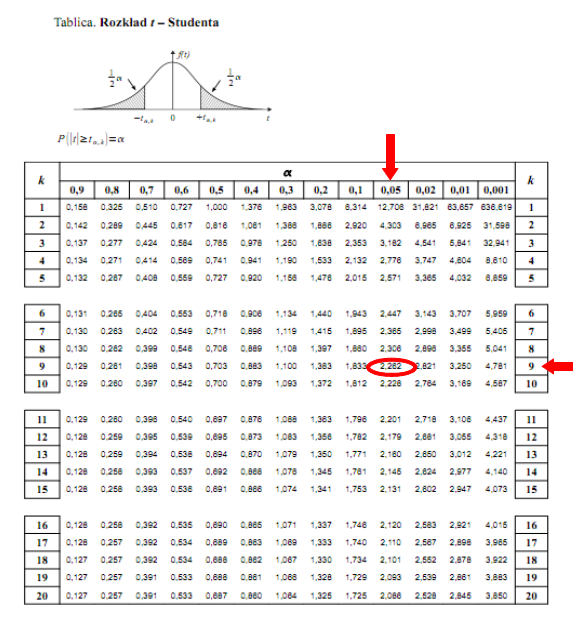
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t , zatem skorzystamy z tablic rozkładu t - Studenta: http://matma-po-ludzku.pl/materialy/statystyka/wzory/tstudent.pdf . Zapis 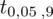oznacza konieczność odnalezienia statystyki dla 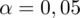i 9 stopni swobody.

Wracamy do obliczeń i podstawiamy do formuły :

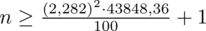
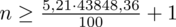
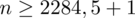
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 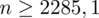, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

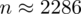Interpretacja brzmi następująco: W celu ustalenia dochodów ludności gminy Pępowo z ufnością 0,95 do próby należy wylosować 2286 mieszkańców (albo dolosować do próby pilotażowej mieszkańców).