Wiadomo, że przeciętny stopień zróżnicowania czasu rozwiązywania pewnego zadania matematycznego wynosi 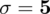minut. Ilu studentów należy wylosować do próby, aby ocenić przeciętny czas rozwiązywania tego zadania z wiarygodnością 0,90 i maksymalnym błędem szacunku 2 minuty?

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

Ilu studentów należy wylosować do próby, aby ocenić przeciętny czas rozwiązywania tego zadania z wiarygodnością 0,90 i maksymalnym błędem szacunku 2 minuty?

Występują tu zwroty: ilu studentów należy wylosować do próby .... , maksymalnym błędem szacunku.... Pojawia się również słowo wiarygodność 0,90 i jest to inaczej współczynnik ufności. Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Wiadomo, że przeciętny stopień zróżnicowania czasu rozwiązywania pewnego zadania matematycznego wynosi minut.

Dowiadujemy się, że zróżnicowanie czasu rozwiązywania pewnego zadania wynosi 5 minut. Mamy podany na tacy symbol 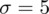co oznacza, że jest to odchylenie standardowe z populacji.

Ilu studentów należy wylosować do próby, aby ocenić przeciętny czas rozwiązywania tego zadania z wiarygodnością 0,90 i maksymalnym błędem szacunku 2 minuty?

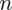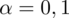Szukamy liczebności próby (liczba studentów), którą oznaczamy literą . Podano również wiarygodność oszacowania, zwaną inaczej współczynnikiem ufności, a więc . Od razu wyznaczamy . Maksymalny błąd szacunku wynosi minuty.

Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA studenci rozwiązujący zadanie	PRÓBA 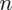wybranych studentów

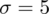
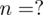
- współczynnik ufności,

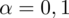
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru cztery modele. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że jest znana , zatem wybieramy model I .

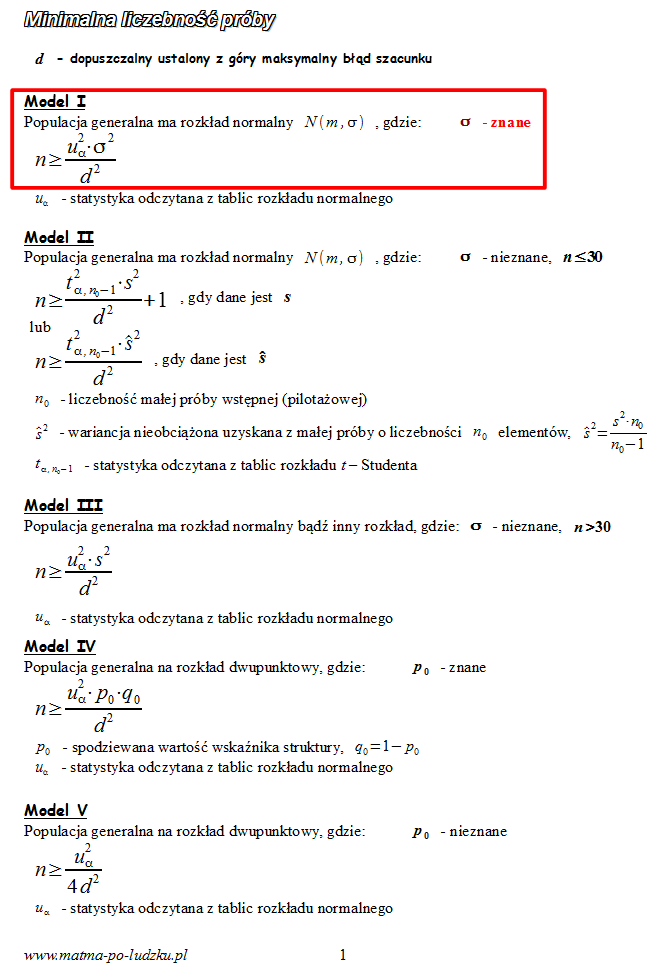
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 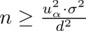konkretnymi liczbami.

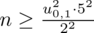
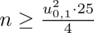
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u , zatem skorzystamy z tablic rozkładu normalnego: http://matma-po-ludzku.pl/materialy/statystyka/wzory/rnormalny.pdf . Zapis 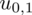oznacza konieczność odnalezienia statystyki dla 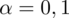. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. 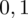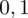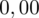W przypadku sumujemy i czyli .

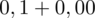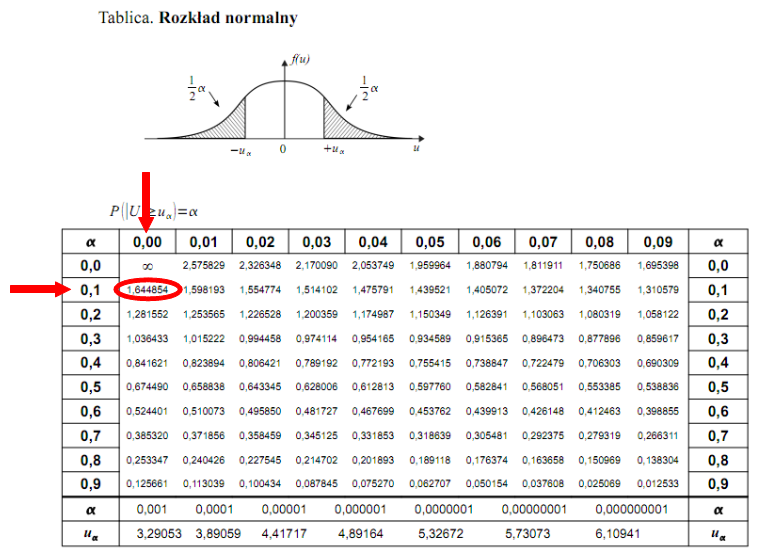
Wracamy do obliczeń i podstawiamy 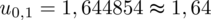(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):

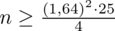
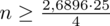
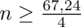
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 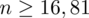, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

Interpretacja brzmi następująco: Aby ocenić przeciętny czas rozwiązywania pewnego zadania matematycznego, z ufnością 0,9 należy wylosować 17 studentów do próby.