Rozkład masy noworodków jest rozkładem normalnym o znanym parametrze 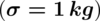. Ile noworodków należy zważyć w klinice położniczej, aby z maksymalnym błędem szacowania 0,25 kg oszacować przeciętną ich masę na poziomie ufności ?

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE MINIMALNEJ LICZEBNOŚCI PRÓBY?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

“ Ile noworodków należy zważyć w klinice położniczej, aby z maksymalnym błędem szacowania 0,25 kg oszacować przeciętną ich masę na poziomie ufności ? ”

Występują tu zwroty: ile noworodków należy zważyć... , z maksymalnym błędem szacowania.... Podano również poziom ufności 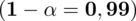. Biorąc pod uwagę wszystkie słowa-klucze mamy na pewno do czynienia z zadaniem dotyczącym minimalnej liczebności próby.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Czytamy zdanie po zdaniu.

Rozkład masy noworodków jest rozkładem normalnym o znanym parametrze .

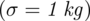Dowiadujemy się, że masa noworodków ma rozkład normalny i ta wzmianka zawsze odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Nie mamy pełnych informacji na temat tego rozkładu, zostało jednak podane odchylenie standardowe dla populacji 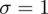kg. Biorąc to wszystko pod uwagę możemy zapisać symbol 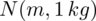oznaczający, że cecha charakteryzuje się rozkładem normalnym o nieznanej średniej 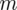i znanym odchyleniu standardowym .

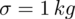“ Ile noworodków należy zważyć w klinice położniczej, aby z maksymalnym błędem szacowania 0,25 kg oszacować przeciętną ich masę na poziomie ufności ? ”

Szukamy liczebności próby (ilość noworodków), którą oznaczamy literą 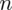. Maksymalny błąd szacunku wynosi 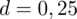kg. Podano również współczynnik ufności, a więc . Od razu wyznaczamy .

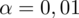Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA noworodki	PRÓBA 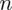wybranych noworodków
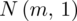- rozkład normalny o nieznanej średniej 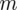i znanym odchyleniu standardowym

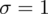
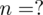
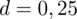
- współczynnik ufności,

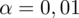
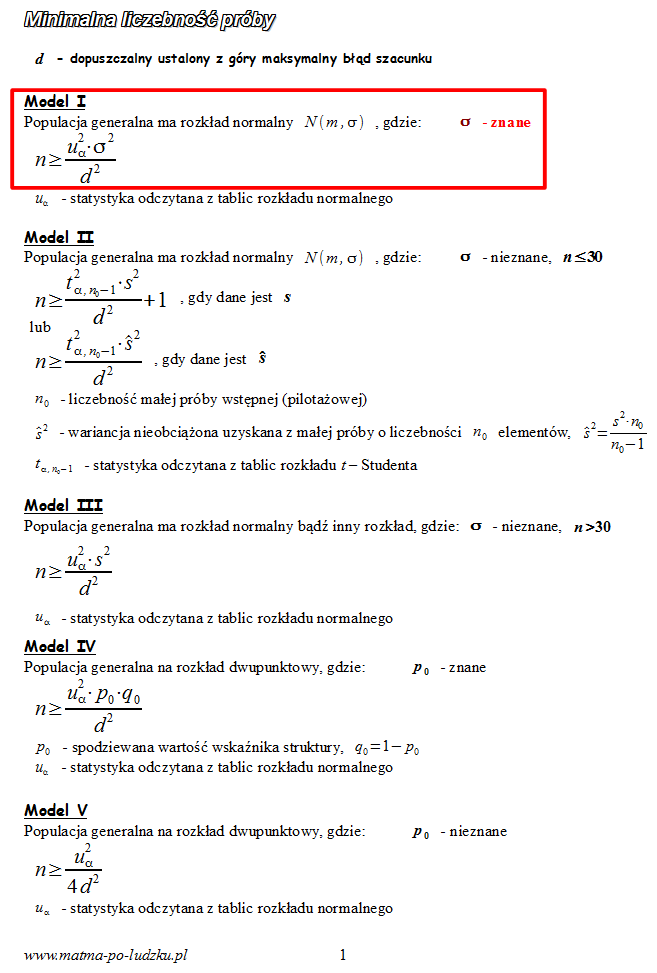
3. WYBÓR ODPOWIEDNIEGO WZORU.

Spójrzmy w kartę wzorów. Dla minimalnej liczebności próby mamy do wyboru pięć modeli. Teraz wracamy do danych i na początku sprawdzamy, czy jest znana. Stwierdzamy, że jest znana , zatem wybieramy model I .

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 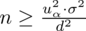konkretnymi liczbami.

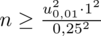
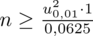
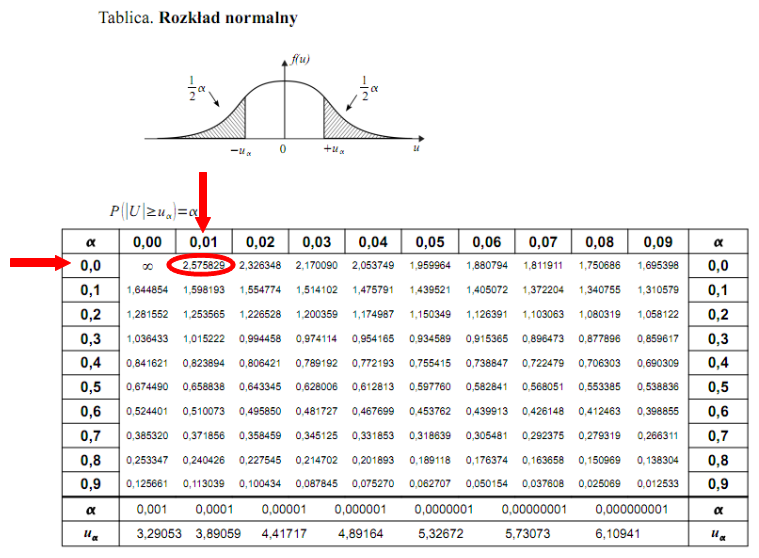
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u , zatem skorzystamy z tablic rozkładu normalnego: http://matma-po-ludzku.pl/materialy/statystyka/wzory/rnormalny.pdf . Zapis 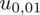oznacza konieczność odnalezienia statystyki dla 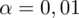. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. 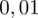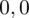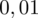W przypadku sumujemy i czyli .

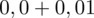Wracamy do obliczeń i podstawiamy 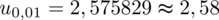(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):

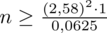
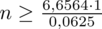
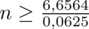
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy: 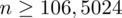, czyli ZAWSZE zaokrąglając w górę otrzymujemy .

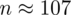Interpretacja brzmi następująco: Aby oszacować przeciętną masę noworodków z ufnością 0,99, do próby należy wylosować 170 noworodków.