
Poniższy szereg rozdzielczy przedstawia strukturę 1000 losowo wybranych mieszkań na osiedlu Ursynów w Warszawie według liczby izb.
Liczba izb w mieszkaniu
|
2
|
3
|
4
|
5
|
6 i więcej
|
Liczba mieszkań
|
96
|
288
|
404
|
168
|
44
|
Oszacowano na podstawie powyższej próby przedział liczbowy dla odsetka lokali 4-izbowych w populacji wszystkich mieszkań na Ursynowie: (37,4%; 43,4%).
1. Jaki współczynnik ufności przyjęto przy konstrukcji powyższego przedziału?
2. Jak zmieni się precyzja oszacowania, jeśli przy założeniu niezmienności struktury próby oraz przy tym samym współczynniku ufności liczebność próby zmniejszymy do 250 mieszkań?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Oszacowano na podstawie powyższej próby przedział liczbowy dla odsetka lokali 4-izbowych w populacji wszystkich mieszkań na Ursynowie: (37,4%; 43,4%).
Występuje tu zwrot: oszacowano przedział - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. W kolejnym zdaniu 1. Jaki współczynnik ufności przyjęto przy konstrukcji powyższego przedziału? znajdujemy dodatkowo wyrażenie: współczynnik ufności.
Podano końcówki przedziału ufności (37,4%; 43,4%), a szukany jest współczynnik ufności z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, w podpunkcie 1) będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje. W podpunkcie 2) po znalezieniu współczynnika ufności zajmiemy się precyzją oszacowania (wybierzemy miarę względną), następnie zmienimy liczebność próby i porównamy wyniki.
Ad. 1)
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
Poniższy szereg rozdzielczy przedstawia strukturę 1000 losowo wybranych mieszkań na osiedlu Ursynów w Warszawie według liczby izb.
Liczba izb w mieszkaniu
|
2
|
3
|
4
|
5
|
6 i więcej
|
Liczba mieszkań
|
96
|
288
|
404
|
168
|
44
|
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości mieszkań spośród wszystkich mieszkań na Ursynowie. Oznaczamy więc liczebność próby
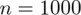 . Dysponujemy również tabelą z danymi, która obrazuje ilość izb w badanych mieszkaniach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje ilość izb w badanych mieszkaniach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
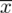 , wariancję
, wariancję
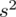 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak całościowo niemożliwe, ponieważ badana cecha (liczba izb w mieszkaniu) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
, itd. W tym przypadku jest to jednak całościowo niemożliwe, ponieważ badana cecha (liczba izb w mieszkaniu) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
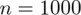 . Dysponujemy również tabelą z danymi, która obrazuje ilość izb w badanych mieszkaniach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje ilość izb w badanych mieszkaniach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
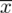 , wariancję
, wariancję
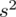 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak całościowo niemożliwe, ponieważ badana cecha (liczba izb w mieszkaniu) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
, itd. W tym przypadku jest to jednak całościowo niemożliwe, ponieważ badana cecha (liczba izb w mieszkaniu) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
Oszacowano na podstawie powyższej próby przedział liczbowy dla odsetka lokali 4-izbowych w populacji wszystkich mieszkań na Ursynowie: (37,4%; 43,4%).
Podano również przedział ufności dla odsetka lokali 4-izbowych. Liczba takich mieszkań (na podstawie tabeli) wynosi 404 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
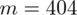 . Szacowany odsetek populacji mieszkań na osiedlu Ursynów mieści się w przedziale od 37,4% do 43,4%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc (0,374; 0,434).
. Szacowany odsetek populacji mieszkań na osiedlu Ursynów mieści się w przedziale od 37,4% do 43,4%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc (0,374; 0,434).
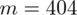 . Szacowany odsetek populacji mieszkań na osiedlu Ursynów mieści się w przedziale od 37,4% do 43,4%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc (0,374; 0,434).
. Szacowany odsetek populacji mieszkań na osiedlu Ursynów mieści się w przedziale od 37,4% do 43,4%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc (0,374; 0,434).
1. Jaki współczynnik ufności przyjęto przy konstrukcji powyższego przedziału?
Naszą niewiadomą jest współczynnik ufności
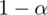 .
.
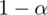 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
wszystkie mieszkania na osiedlu Ursynów w Warszawie |
PRÓBA
1000 wybranych mieszkań |
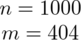
|
(0,374; 0,434) - końcówki przedziału ufności dla odsetka z populacji
 - współczynnik ufności,
- współczynnik ufności,
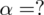
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
Oszacowano na podstawie powyższej próby przedział liczbowy dla odsetka lokali 4-izbowych w populacji wszystkich mieszkań na Ursynowie: (37,4%; 43,4%).
Słowo odsetek oznacza, że przedział ufności zbudowano dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
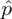 .
.
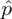 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
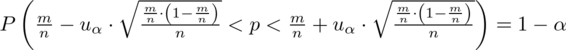 konkretnymi danymi.
konkretnymi danymi.
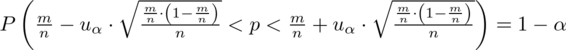 konkretnymi danymi.
konkretnymi danymi.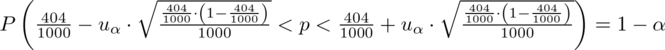
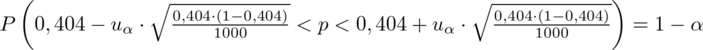
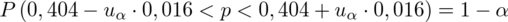
Jak widać, nie możemy uzupełnić współczynnika ufności
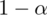 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.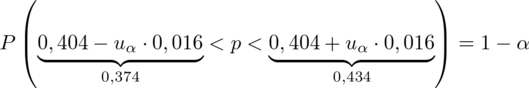
Nie znamy wartości
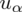 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,374 czy 0,434? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,374 czy 0,434? Jest to całkowicie obojętne, ponieważ w obu przypadkach
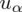 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
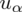 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,374 czy 0,434? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,374 czy 0,434? Jest to całkowicie obojętne, ponieważ w obu przypadkach
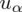 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład: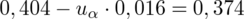
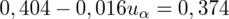

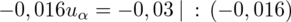

Wyliczona wartość statystyki może się różnić, ponieważ wcześniejsze obliczenia dały
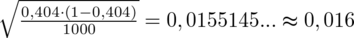
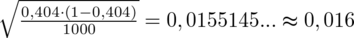
Jeśli komuś z Was jest wygodniej rozwiązywać równania z literką x, to może nią spokojnie na początku zastąpić symbol
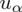 .
.
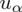 .
.
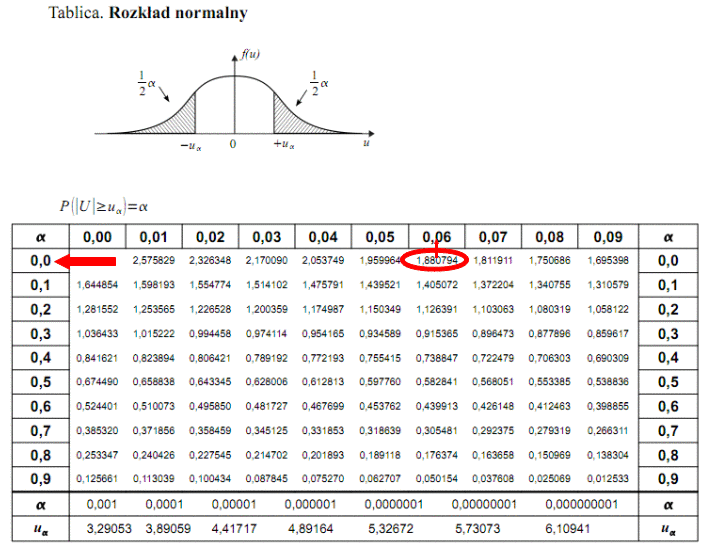
Dopiero teraz wracamy do odczytywania z tablic, jest to tzw. „zadanie od tyłu”, więc i z tablic czytamy od tyłu, a więc szukamy wartości najbliższej
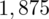 , ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
, ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
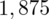 we wnętrzu tablicy stanowi
we wnętrzu tablicy stanowi
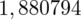 . Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
. Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
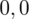 i
i
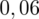 , czyli
, czyli
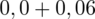 . Pamiętajmy, że jest to
. Pamiętajmy, że jest to
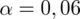 .
.
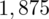 , ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
, ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
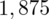 we wnętrzu tablicy stanowi
we wnętrzu tablicy stanowi
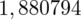 . Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
. Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
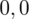 i
i
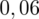 , czyli
, czyli
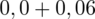 . Pamiętajmy, że jest to
. Pamiętajmy, że jest to
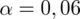 .
.
Ad. 2)
Definiujemy wzór na względną precyzję oszacowania wskaźnika struktury
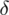 .
.
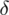 .
.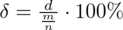 lub
lub
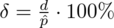 , gdzie
, gdzie
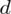 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
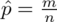 :
: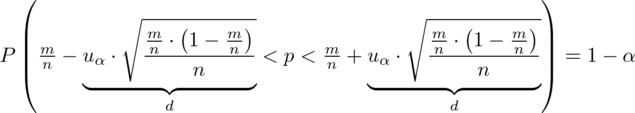
czyli
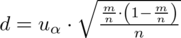 .
.
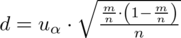 .
.
Powtarzam jeszcze raz, że formuła na obliczenie
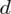 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
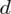 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
Na początku określimy względną precyzję szacunku przy danych
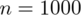 i wyliczonej w pierwszym podpunkcie
i wyliczonej w pierwszym podpunkcie
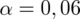 .
.
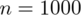 i wyliczonej w pierwszym podpunkcie
i wyliczonej w pierwszym podpunkcie
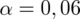 .
.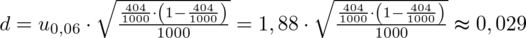 , gdzie
, gdzie
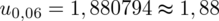 (z tablicy wyżej)
(z tablicy wyżej)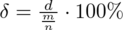
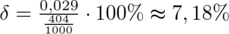
Teraz wyliczymy względną precyzję szacunku dla próby o liczebności
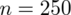 ,
,
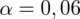 i założeniu niezmienności struktury. Co oznacza owa niezmienność struktury? W próbie o liczebności 1000 były 404 mieszkania 4-izbowe, a więc wskaźnik struktury w próbie wynosi
i założeniu niezmienności struktury. Co oznacza owa niezmienność struktury? W próbie o liczebności 1000 były 404 mieszkania 4-izbowe, a więc wskaźnik struktury w próbie wynosi
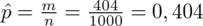 i to on nie powinien ulec zmianie. Przy nowej liczebności próby można oczywiście policzyć ile będzie proporcjonalnie mieszkań 4-izbowych, ale nie jest to konieczne. Tym razem skorzystamy ze wzoru
i to on nie powinien ulec zmianie. Przy nowej liczebności próby można oczywiście policzyć ile będzie proporcjonalnie mieszkań 4-izbowych, ale nie jest to konieczne. Tym razem skorzystamy ze wzoru
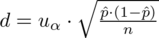 dla wygody.
dla wygody.
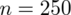 ,
,
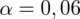 i założeniu niezmienności struktury. Co oznacza owa niezmienność struktury? W próbie o liczebności 1000 były 404 mieszkania 4-izbowe, a więc wskaźnik struktury w próbie wynosi
i założeniu niezmienności struktury. Co oznacza owa niezmienność struktury? W próbie o liczebności 1000 były 404 mieszkania 4-izbowe, a więc wskaźnik struktury w próbie wynosi
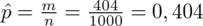 i to on nie powinien ulec zmianie. Przy nowej liczebności próby można oczywiście policzyć ile będzie proporcjonalnie mieszkań 4-izbowych, ale nie jest to konieczne. Tym razem skorzystamy ze wzoru
i to on nie powinien ulec zmianie. Przy nowej liczebności próby można oczywiście policzyć ile będzie proporcjonalnie mieszkań 4-izbowych, ale nie jest to konieczne. Tym razem skorzystamy ze wzoru
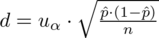 dla wygody.
dla wygody. 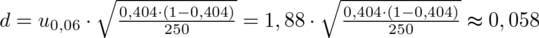 , gdzie
, gdzie
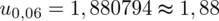 (z tablicy wyżej)
(z tablicy wyżej)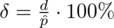
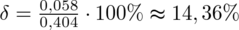
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy w podpunkcie 1):
Przy konstrukcji powyższego przedziału przyjęto współczynnik ufności około
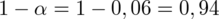 .
.
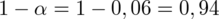 .
.
Ostatecznie otrzymujemy w podpunkcie 2):
Po zmianie liczebności próby z 1000 mieszkań do 250 mieszkań precyzja oszacowania zmalała z 7,18% do 14,36%, a więc dwukrotnie. Coś tu jednak się nie zgadza, prawda? Przecież po zmianie liczebności próby otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im mniejsza wartość liczbowa otrzymana w wyniku tym lepsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku w tym przypadku jest spowodowane zbyt małą liczebnością próby.
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4