
W pewnym zakładzie odzieżowym zbadano 1000 wyrobów spośród nowo wyprodukowanej partii i otrzymano następujący rozkład liczby usterek:
Liczba usterek
|
0
|
1
|
2
|
3
|
4
|
5
|
Liczba wyrobów
|
280
|
260
|
200
|
160
|
70
|
30
|
Wyznaczyć na poziomie ufności 0,9 przedział ufności dla odsetka wyrobów bez usterek oraz obliczyć i zinterpretować względny błąd losowy. Jak zmieni się względny błąd losowy, jeśli poziom ufności wyniesie 0,95?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Wyznaczyć na poziomie ufności 0,9 przedział ufności dla odsetka wyrobów bez usterek oraz obliczyć i zinterpretować względny błąd losowy.
Występują tu zwroty: wyznaczyć przedział ufności i poziom ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
Dodatkowo interesuje nas względny błąd losowy, a pytanie o tą wielkość dotyczy z reguły zadań z estymacji. Do stworzenia wzoru na względną precyzję szacunku potrzebujemy formuły na ten przedział. Będziemy postępować zgodnie ze znanym schematem dotyczącym estymacji przedziałowej i dodatkowo policzymy względny błąd losowy - najpierw dla współczynnika ufności równego 0,9, a później dla 0,95. Na końcu porównamy wyniki.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W pewnym zakładzie odzieżowym zbadano 1000 wyrobów spośród nowo wyprodukowanej partii i otrzymano następujący rozkład liczby usterek:
Liczba usterek
|
0
|
1
|
2
|
3
|
4
|
5
|
Liczba wyrobów
|
280
|
260
|
200
|
160
|
70
|
30
|
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat zbadania konkretnej ilości wyrobów spośród całej wyprodukowanej partii. Oznaczamy więc liczebność próby
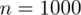 . Dysponujemy również tabelą z danymi, która obrazuje liczbę usterek w poszczególnych wyrobach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje liczbę usterek w poszczególnych wyrobach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
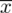 , wariancję
, wariancję
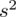 , odchylenie standardowe
, odchylenie standardowe
 , itd. Na razie jednak nie będziemy ich wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
, itd. Na razie jednak nie będziemy ich wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
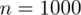 . Dysponujemy również tabelą z danymi, która obrazuje liczbę usterek w poszczególnych wyrobach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje liczbę usterek w poszczególnych wyrobach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
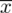 , wariancję
, wariancję
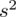 , odchylenie standardowe
, odchylenie standardowe
 , itd. Na razie jednak nie będziemy ich wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
, itd. Na razie jednak nie będziemy ich wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
Wyznaczyć na poziomie ufności 0,9 przedział ufności dla odsetka wyrobów bez usterek oraz obliczyć i zinterpretować względny błąd losowy.
Podano poziom ufności
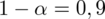 i od razu wyznaczamy
i od razu wyznaczamy
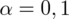 . Dowiadujemy się również, że trzeba zbudować przedział ufności dla odetka wyrobów bez usterek, czyli (zgodnie z tabelą) 0 usterek. Liczba takich wyrobów (na podstawie tabeli) wynosi 280 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Dowiadujemy się również, że trzeba zbudować przedział ufności dla odetka wyrobów bez usterek, czyli (zgodnie z tabelą) 0 usterek. Liczba takich wyrobów (na podstawie tabeli) wynosi 280 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
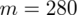 .
.
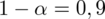 i od razu wyznaczamy
i od razu wyznaczamy
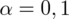 . Dowiadujemy się również, że trzeba zbudować przedział ufności dla odetka wyrobów bez usterek, czyli (zgodnie z tabelą) 0 usterek. Liczba takich wyrobów (na podstawie tabeli) wynosi 280 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Dowiadujemy się również, że trzeba zbudować przedział ufności dla odetka wyrobów bez usterek, czyli (zgodnie z tabelą) 0 usterek. Liczba takich wyrobów (na podstawie tabeli) wynosi 280 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
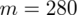 .
.
Jak zmieni się względny błąd losowy, jeśli poziom ufności wyniesie 0,95?
Podano nową wartość poziomu ufności
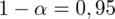 ,
,
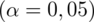 , dla której wyliczymy względny błąd losowy.
, dla której wyliczymy względny błąd losowy.
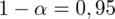 ,
,
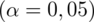 , dla której wyliczymy względny błąd losowy.
, dla której wyliczymy względny błąd losowy.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
nowo wyprodukowana partia wyrobów odzieżowych |
PRÓBA
1000 wybranych wyrobów |
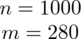
|
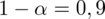 - współczynnik ufności,
- współczynnik ufności,
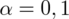
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
Wyznaczyć na poziomie ufności 0,9 przedział ufności dla odsetka wyrobów bez usterek oraz obliczyć i zinterpretować względny błąd losowy.
Słowo odsetek oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
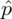 .
.
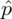 .
.
Nadszedł czas by określić wzór na względny błąd losowy wskaźnika struktury
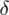 .
.
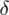 .
.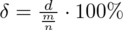 lub
lub
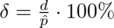 , gdzie
, gdzie
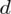 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
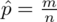 :
: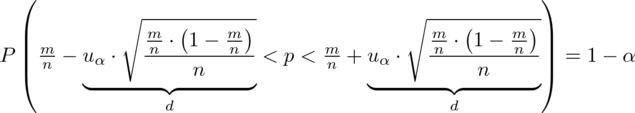
czyli
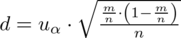 .
.
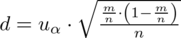 .
.
Powtarzam jeszcze raz, że formuła na obliczenie
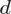 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
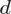 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
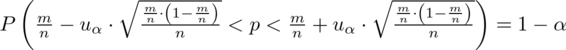 konkretnymi danymi.
konkretnymi danymi.
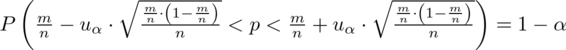 konkretnymi danymi.
konkretnymi danymi.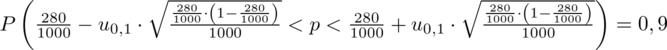
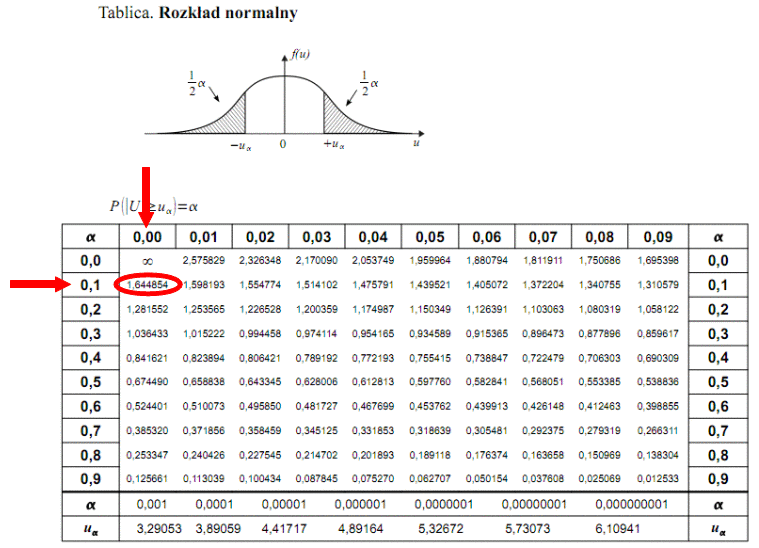
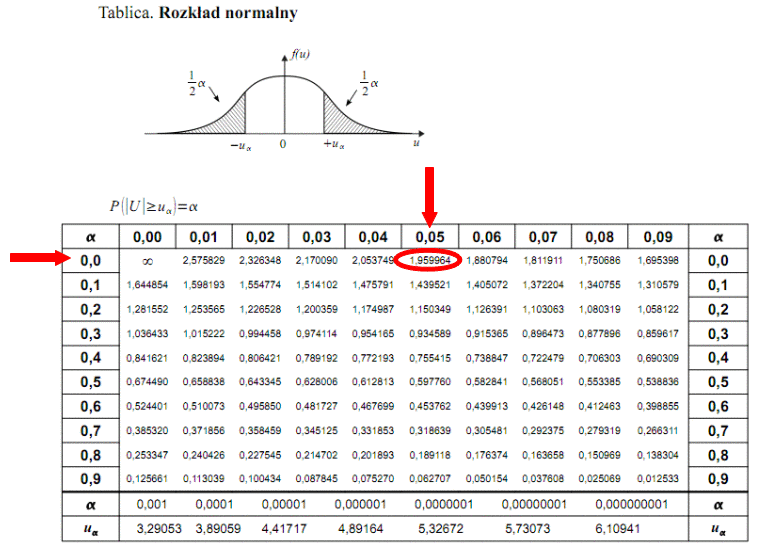
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
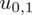 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
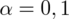 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
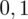 sumujemy
sumujemy
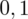 i
i
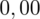 czyli
czyli
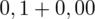 .
.
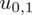 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
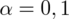 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
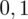 sumujemy
sumujemy
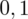 i
i
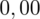 czyli
czyli
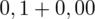 .
.
Wracamy do obliczeń i podstawiamy
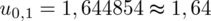 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
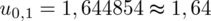 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):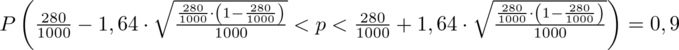
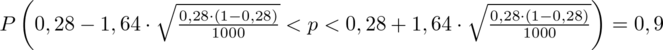
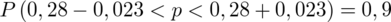
Z kolei względna precyzja szacunku dla
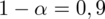 ,
,
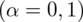 :
:
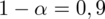 ,
,
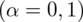 :
: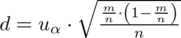
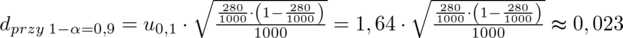
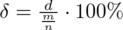
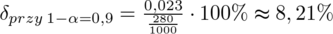
Teraz policzymy precyzję oszacowania dla współczynnika ufności
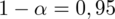 ,
,
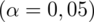 . Szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
. Szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
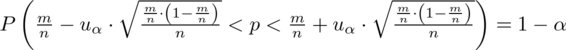 i tym samym formuła na względny błąd szacunku nie ulega zmianie.
i tym samym formuła na względny błąd szacunku nie ulega zmianie.
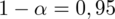 ,
,
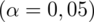 . Szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
. Szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
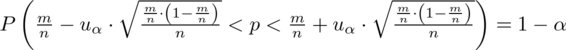 i tym samym formuła na względny błąd szacunku nie ulega zmianie.
i tym samym formuła na względny błąd szacunku nie ulega zmianie.
Po wstawieniu danych otrzymujemy:
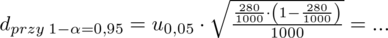
Brakuje odpowiedniej statystyki z tablic. W formule znajduje się literka u, zatem ponownie skorzystamy z tablic rozkładu normalnego (link). Zapis
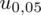 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
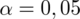 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
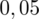 sumujemy
sumujemy
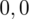 i
i
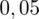 czyli
czyli
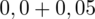 .
.
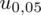 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
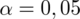 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
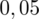 sumujemy
sumujemy
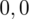 i
i
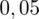 czyli
czyli
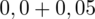 .
.
Wracamy do obliczeń i podstawiamy
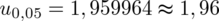 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
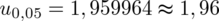 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
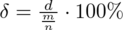
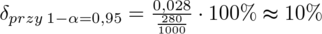
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
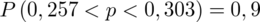
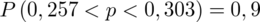
Interpretacja brzmi następująco: Z ufnością 0,9 odsetek wyrobów bez usterek w całej nowo wyprodukowanej partii odzieży mieści się w przedziale od 0,257 do 0,303.
Natomiast względny błąd losowy
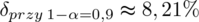 i
i
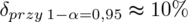
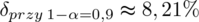 i
i
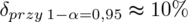
Interpretacja brzmi następująco:
Po zwiększeniu współczynnika ufności z 0,9 to 0,95 procentowa wartość względnego błędu losowego ulega zmniejszeniu i to jest uniwersalna zasada. Coś tu jednak się nie zgadza, prawda? Przecież otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im mniejsza wartość liczbowa otrzymana w wyniku tym lepsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku może być spowodowane zbyt wysokim współczynnikiem ufności, zbyt małą liczebnością próby oraz wysokim zróżnicowaniem wyników w próbie (np. duży rozstrzał danych).
Zadanie pochodzi z: Statystyka : elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka. Wyd. 6 popr., Wrocław : Wydawnictwo Akademii Ekonomicznej, 2006. - 455 s.: il.; 24 cm. ISBN 83-7011-783-X