
Na podstawie 200-elementowej próby prostej otrzymano następującą strukturę gospodarstw domowych, według liczby osób w gospodarstwie (dane umowne):
Liczba osób w gospodarstwie
|
1
|
2
|
3
|
4
|
5
|
6 i więcej
|
Odsetek gospodarstw
|
0,20
|
0,24
|
0,29
|
0,12
|
0,11
|
0,04
|
Na poziomie ufności 0,99 wyznaczyć przedział ufności dla frakcji gospodarstw domowych, liczących co najwyżej 3 osoby.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Na poziomie ufności 0,99 wyznaczyć przedział ufności dla frakcji gospodarstw domowych, liczących co najwyżej 3 osoby.
Występuje tu zwroty: wyznaczyć przedział ufności i poziom ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
Na podstawie 200-elementowej próby prostej otrzymano następującą strukturę gospodarstw domowych, według liczby osób w gospodarstwie (dane umowne):
Liczba osób w gospodarstwie
|
1
|
2
|
3
|
4
|
5
|
6 i więcej
|
Odsetek gospodarstw
|
0,20
|
0,24
|
0,29
|
0,12
|
0,11
|
0,04
|
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości jednostek spośród wszystkich gospodarstw domowych. Oznaczamy więc liczebność próby
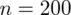 . Dysponujemy również tabelą z danymi, która obrazuje ilość osób w badanych gospodarstwach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje ilość osób w badanych gospodarstwach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
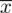 , wariancję
, wariancję
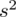 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak częściowo niemożliwe, ponieważ badana cecha (liczba osób w gospodarstwie) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
, itd. W tym przypadku jest to jednak częściowo niemożliwe, ponieważ badana cecha (liczba osób w gospodarstwie) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
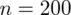 . Dysponujemy również tabelą z danymi, która obrazuje ilość osób w badanych gospodarstwach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
. Dysponujemy również tabelą z danymi, która obrazuje ilość osób w badanych gospodarstwach. Na podstawie tabeli jesteśmy w stanie policzyć różne parametry dla próby np. średnią
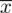 , wariancję
, wariancję
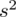 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak częściowo niemożliwe, ponieważ badana cecha (liczba osób w gospodarstwie) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
, itd. W tym przypadku jest to jednak częściowo niemożliwe, ponieważ badana cecha (liczba osób w gospodarstwie) w ostatniej kolumnie ma wartość 6 i więcej, a w obliczeniach stricte liczbowych taka wartość nie wchodzi w grę. Na razie jednak nie martwmy się i nie wyliczajmy żadnych parametrów próby na zapas, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru dowiemy się, które parametry próby będą nas interesowały.
Na poziomie ufności 0,99 wyznaczyć przedział ufności dla frakcji gospodarstw domowych, liczących co najwyżej 3 osoby.
Podano poziom ufności
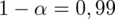 i od razu wyznaczamy
i od razu wyznaczamy
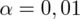 . Uzyskujemy również informację, że trzeba zbudować przedział ufności dla frakcji gospodarstw liczących co najwyżej 3 osoby, a więc może to być (zgodnie z tabelą) 1, 2 lub 3 osoby. Ich odsetek (na podstawie tabeli) to odpowiednio 0,20, 0,24 i 0,29. Sumując otrzymujemy
. Uzyskujemy również informację, że trzeba zbudować przedział ufności dla frakcji gospodarstw liczących co najwyżej 3 osoby, a więc może to być (zgodnie z tabelą) 1, 2 lub 3 osoby. Ich odsetek (na podstawie tabeli) to odpowiednio 0,20, 0,24 i 0,29. Sumując otrzymujemy
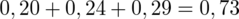 - jest to łączny odsetek obserwacji spośród próby. Opisujemy go symbolem
- jest to łączny odsetek obserwacji spośród próby. Opisujemy go symbolem
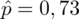 .
.
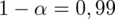 i od razu wyznaczamy
i od razu wyznaczamy
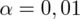 . Uzyskujemy również informację, że trzeba zbudować przedział ufności dla frakcji gospodarstw liczących co najwyżej 3 osoby, a więc może to być (zgodnie z tabelą) 1, 2 lub 3 osoby. Ich odsetek (na podstawie tabeli) to odpowiednio 0,20, 0,24 i 0,29. Sumując otrzymujemy
. Uzyskujemy również informację, że trzeba zbudować przedział ufności dla frakcji gospodarstw liczących co najwyżej 3 osoby, a więc może to być (zgodnie z tabelą) 1, 2 lub 3 osoby. Ich odsetek (na podstawie tabeli) to odpowiednio 0,20, 0,24 i 0,29. Sumując otrzymujemy
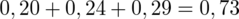 - jest to łączny odsetek obserwacji spośród próby. Opisujemy go symbolem
- jest to łączny odsetek obserwacji spośród próby. Opisujemy go symbolem
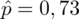 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
gospodarstwa domowe |
PRÓBA
200 wybranych gospodarstw |
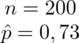
|
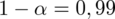 - współczynnik ufności,
- współczynnik ufności,
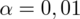
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
Na poziomie ufności 0,99 wyznaczyć przedział ufności dla frakcji gospodarstw domowych, liczących co najwyżej 3 osoby.
Słowo frakcja oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy do wyboru dwie formuły. W danych wypisano
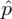 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
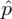 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
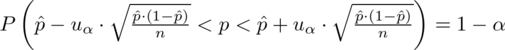 konkretnymi danymi.
konkretnymi danymi.
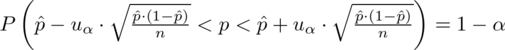 konkretnymi danymi.
konkretnymi danymi.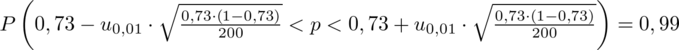
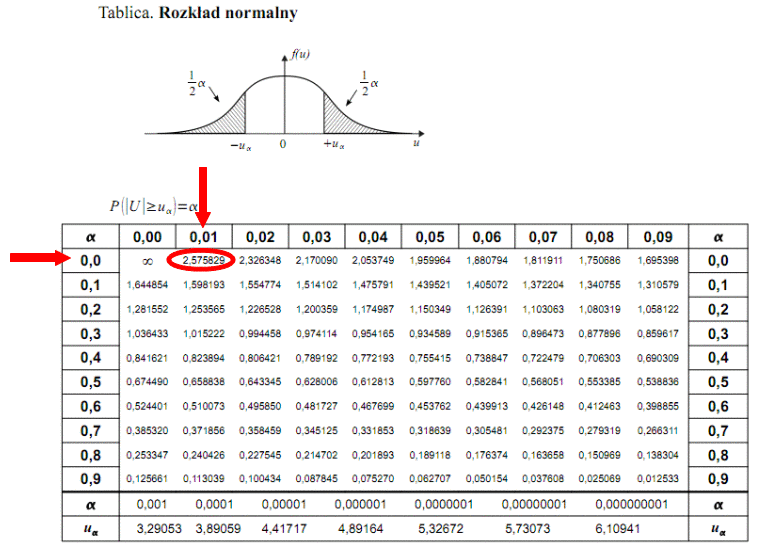
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
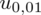 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
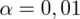 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
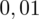 sumujemy
sumujemy
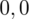 i
i
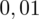 czyli
czyli
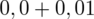 .
.
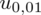 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
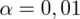 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
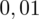 sumujemy
sumujemy
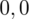 i
i
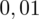 czyli
czyli
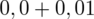 .
.
Wracamy do obliczeń i podstawiamy
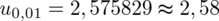 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
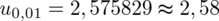 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)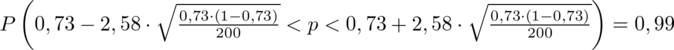
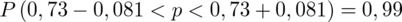
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
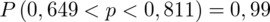
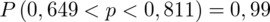
Interpretacja brzmi następująco: Z ufnością 0,99 frakcja gospodarstw domowych, liczących co najwyżej 3 osoby mieści się w przedziale od 0,649 do 0,811.
Zadanie pochodzi z: Statystyka : elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka. Wyd. 6 popr., Wrocław : Wydawnictwo Akademii Ekonomicznej, 2006. - 455 s.: il.; 24 cm. ISBN 83-7011-783-X