
Spośród pracowników uczelni ekonomicznych wylosowano 320 osób i zapytano o znajomość języków obcych. Jedno z pytań brzmiało: wybierz (jeden) język, którym chciałbyś się posługiwać na najbliżej konferencji międzynarodowej. Odpowiedzi zaprezentowano w następującej postaci:
Język
|
angielski
|
francuski
|
niemiecki
|
rosyjski
|
włoski
|
Liczba osób
|
120
|
50
|
100
|
30
|
20
|
Przyjmując współczynnik ufności równy 0,95, zbudować przedział ufności dla frakcji pracowników, którzy chcieliby na konferencji posługiwać się językiem francuskim.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Przyjmując współczynnik ufności równy 0,95, zbudować przedział ufności dla frakcji pracowników, którzy chcieliby na konferencji posługiwać się językiem francuskim.
Występuje tu zwroty: zbudować przedział ufności i współczynnik ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
Spośród pracowników uczelni ekonomicznych wylosowano 320 osób i zapytano o znajomość języków obcych.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości osób spośród wszystkich pracowników uczelni ekonomicznych. Oznaczamy więc liczebność próby
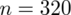 .
.
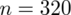 .
.
Jedno z pytań brzmiało: wybierz (jeden) język, którym chciałbyś się posługiwać na najbliżej konferencji międzynarodowej.
W tym zdaniu nie ma danych liczbowych, więc je pomijamy.
Odpowiedzi zaprezentowano w następującej postaci:
Język
|
angielski
|
francuski
|
niemiecki
|
rosyjski
|
włoski
|
Liczba osób
|
120
|
50
|
100
|
30
|
20
|
Dysponujemy tabelą z danymi, która obrazuje języki preferowane przez poszczególne osoby. Na ogół dysponując tabelą jesteśmy w stanie policzyć różne parametry dla próby np. średnią
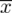 , wariancję
, wariancję
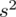 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak niemożliwe, ponieważ badana cecha (język) jest cechą jakościową, a nie ilościową (liczba). Na chłopski rozum przecież trudno wyliczyć chociażby średnią mając języki obce i ilość ludzi się nimi posługującymi - jest to niewykonalne i nielogiczne.
, itd. W tym przypadku jest to jednak niemożliwe, ponieważ badana cecha (język) jest cechą jakościową, a nie ilościową (liczba). Na chłopski rozum przecież trudno wyliczyć chociażby średnią mając języki obce i ilość ludzi się nimi posługującymi - jest to niewykonalne i nielogiczne.
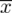 , wariancję
, wariancję
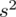 , odchylenie standardowe
, odchylenie standardowe
 , itd. W tym przypadku jest to jednak niemożliwe, ponieważ badana cecha (język) jest cechą jakościową, a nie ilościową (liczba). Na chłopski rozum przecież trudno wyliczyć chociażby średnią mając języki obce i ilość ludzi się nimi posługującymi - jest to niewykonalne i nielogiczne.
, itd. W tym przypadku jest to jednak niemożliwe, ponieważ badana cecha (język) jest cechą jakościową, a nie ilościową (liczba). Na chłopski rozum przecież trudno wyliczyć chociażby średnią mając języki obce i ilość ludzi się nimi posługującymi - jest to niewykonalne i nielogiczne.
Przyjmując współczynnik ufności równy 0,95, zbudować przedział ufności dla frakcji pracowników, którzy chcieliby na konferencji posługiwać się językiem francuskim.
Dopiero tu uzyskujemy informację, że trzeba zbudować przedział ufności dla frakcji osób posługujących się językiem francuskim. Ich ilość (na podstawie tabeli) to 50 - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
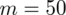 . Podano również współczynnik ufności
. Podano również współczynnik ufności
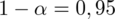 i od razu wyznaczamy
i od razu wyznaczamy
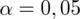 .
.
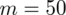 . Podano również współczynnik ufności
. Podano również współczynnik ufności
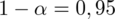 i od razu wyznaczamy
i od razu wyznaczamy
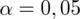 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
pracownicy uczelni ekonomicznych |
PRÓBA
320 wybranych osób |
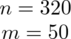
|
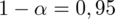 - współczynnik ufności,
- współczynnik ufności,
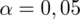
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
Przyjmując współczynnik ufności równy 0,95, zbudować przedział ufności dla frakcji pracowników, którzy chcieliby na konferencji posługiwać się językiem francuskim.
Słowo frakcja oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
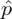 .
.
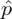 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
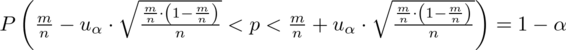 konkretnymi danymi.
konkretnymi danymi.
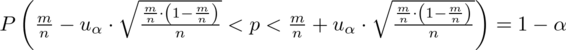 konkretnymi danymi.
konkretnymi danymi.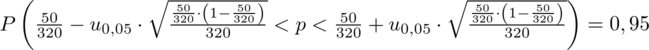
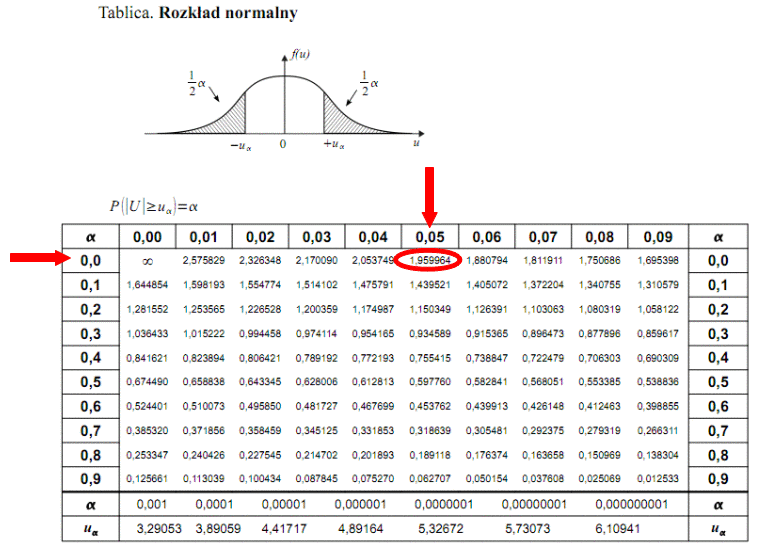
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
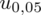 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
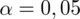 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
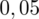 sumujemy
sumujemy
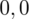 i
i
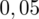 czyli
czyli
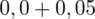 .
.
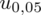 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
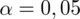 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
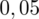 sumujemy
sumujemy
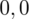 i
i
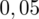 czyli
czyli
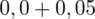 .
.
Wracamy do obliczeń i podstawiamy
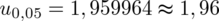 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
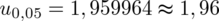 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)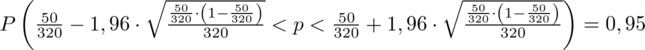
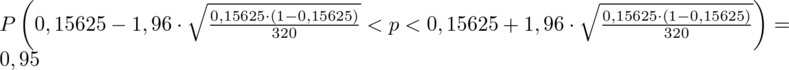
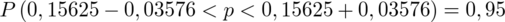
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
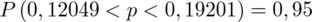
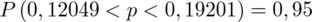
Interpretacja brzmi następująco: Z ufnością 0,95 frakcja pracowników, którzy chcieliby na konferencji posługiwać się językiem francuskim mieści się w przedziale od 0,12049 do 0,19201.
Zadanie pochodzi z: Statystyka ogólna w zadaniach / Woźniak Michał, Wyd. 2, Kraków: Wydawnictwo Akademii Ekonomicznej w Krakowie, ISBN: 978-83-7252-474-4