Rozkład liczby filiżanek kawy, wypijanych w ciągu dnia, przedstawia tabela:
Liczba filiżanek kawy
|
0
|
1
|
2
|
3
|
4
|
Liczba osób
|
14
|
28
|
36
|
28
|
14
|
Na poziomie ufności 0,95 wyznaczyć przedział ufności dla frakcji osób, które:
a) wypijają do dwóch filiżanek kawy dziennie (włącznie)
b) wypijają co najmniej 3 filiżanki kawy dziennie.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Na poziomie ufności 0,95 wyznaczyć przedział ufności dla frakcji osób, które: ...
Występują tu zwroty: wyznaczyć przedział ufności i poziom ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
Rozkład liczby filiżanek kawy, wypijanych w ciągu dnia, przedstawia tabela:
Liczba filiżanek kawy
|
0
|
1
|
2
|
3
|
4
|
Liczba osób
|
14
|
28
|
36
|
28
|
14
|
Dysponujemy tabelą z danymi, na podstawie których można policzyć różne parametry dla próby np. średnią
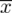 , wariancję
, wariancję
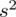 , odchylenie standardowe
, odchylenie standardowe
 , itd. Skąd wiemy, że jest to próba, a nie populacja? Populacja jest z reguły ogromną zbiorowością i jako całość jest niemożliwa do 100% zbadania. Tak więc mając w zadaniu tabelkę zawsze przyjmujemy, że jest to próba (chyba, że wyraźnie napisano, że tabela dotyczy populacji). Od razu możemy określić liczebność próby sumując liczbę osób pytanych o spożycie kawy w ciągu dnia, czyli
, itd. Skąd wiemy, że jest to próba, a nie populacja? Populacja jest z reguły ogromną zbiorowością i jako całość jest niemożliwa do 100% zbadania. Tak więc mając w zadaniu tabelkę zawsze przyjmujemy, że jest to próba (chyba, że wyraźnie napisano, że tabela dotyczy populacji). Od razu możemy określić liczebność próby sumując liczbę osób pytanych o spożycie kawy w ciągu dnia, czyli
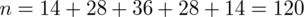 . Innych parametrów próby na razie nie będziemy wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
. Innych parametrów próby na razie nie będziemy wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
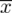 , wariancję
, wariancję
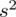 , odchylenie standardowe
, odchylenie standardowe
 , itd. Skąd wiemy, że jest to próba, a nie populacja? Populacja jest z reguły ogromną zbiorowością i jako całość jest niemożliwa do 100% zbadania. Tak więc mając w zadaniu tabelkę zawsze przyjmujemy, że jest to próba (chyba, że wyraźnie napisano, że tabela dotyczy populacji). Od razu możemy określić liczebność próby sumując liczbę osób pytanych o spożycie kawy w ciągu dnia, czyli
, itd. Skąd wiemy, że jest to próba, a nie populacja? Populacja jest z reguły ogromną zbiorowością i jako całość jest niemożliwa do 100% zbadania. Tak więc mając w zadaniu tabelkę zawsze przyjmujemy, że jest to próba (chyba, że wyraźnie napisano, że tabela dotyczy populacji). Od razu możemy określić liczebność próby sumując liczbę osób pytanych o spożycie kawy w ciągu dnia, czyli
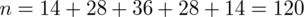 . Innych parametrów próby na razie nie będziemy wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
. Innych parametrów próby na razie nie będziemy wyliczać, ponieważ może się okazać, że jest to niepotrzebne. Dopiero po wybraniu odpowiedniego wzoru okaże się, które parametry próby będą nas interesowały.
Na poziomie ufności 0,95 wyznaczyć przedział ufności dla frakcji osób, które:
Podano współczynnik ufności
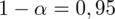 i od razu wyznaczamy
i od razu wyznaczamy
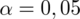 .
.
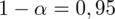 i od razu wyznaczamy
i od razu wyznaczamy
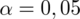 .
.
Na tym etapie zaczniemy równolegle robić dwa podpunkty zdania:
Ad. a)
a) wypijają do dwóch filiżanek kawy dziennie (włącznie)
Wybieramy z tabeli liczbę osób, które wypijają do dwóch filiżanek kawy dziennie. Oznacza to 0, 1 lub 2 filiżanki. Ilości osób odpowiadające podanym ilościom filiżanek to 14, 28 i 36. Sumując je otrzymujemy
 osób - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
osób - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
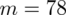 .
.
 osób - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
osób - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
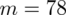 .
.
Ad. b)
b) wypijają co najmniej 3 filiżanki kawy dziennie.
Wybieramy z tabeli liczbę osób, które wypijają co najmniej 3 filiżanki kawy dziennie. Oznacza to 3 lub 4 filiżanki (większej ilości w tabeli nie ma). Ilości osób odpowiadające podanym ilościom filiżanek to 28 i 14. Sumując je otrzymujemy
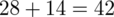 osoby - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
osoby - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
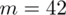 .
.
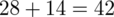 osoby - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
osoby - jest to ilość obserwacji spośród próby. Oznaczamy ją symbolem
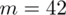 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
osoby spożywające napoje |
PRÓBA
120 wybranych osób |
||
|
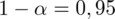 - współczynnik ufności,
- współczynnik ufności,
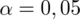
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności wyłapując w zadaniu słowo:
Na poziomie ufności 0,95 wyznaczyć przedział ufności dla frakcji osób, które:
Słowo frakcja oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji (dla obydwu podpunktów). Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
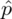 .
.
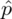 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
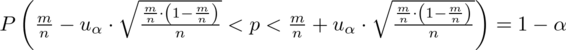 konkretnymi danymi.
konkretnymi danymi.
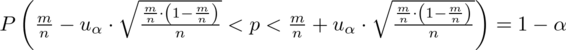 konkretnymi danymi.
konkretnymi danymi.
Ad. a)
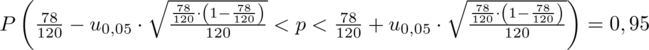
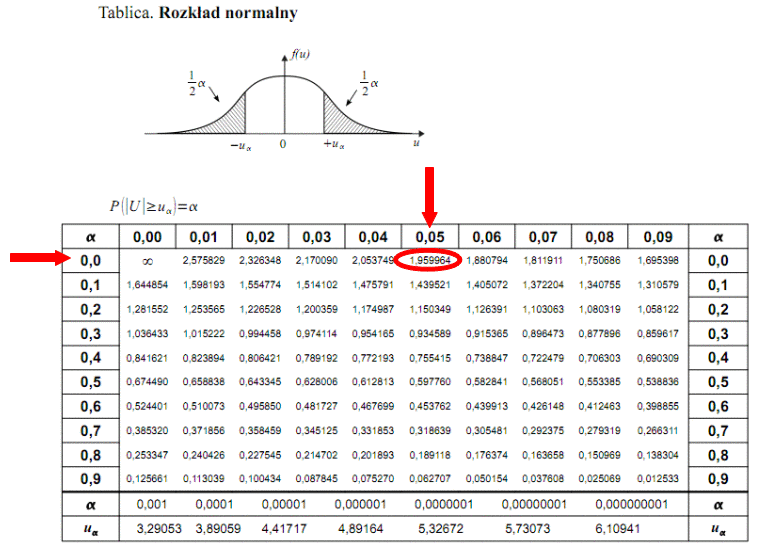
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
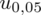 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
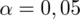 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
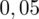 sumujemy
sumujemy
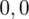 i
i
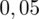 czyli
czyli
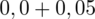 .
.
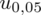 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
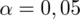 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
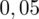 sumujemy
sumujemy
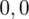 i
i
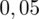 czyli
czyli
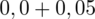 .
.
Wracamy do obliczeń i podstawiamy
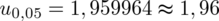 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
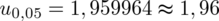 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)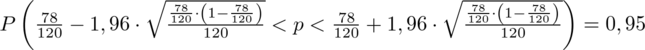
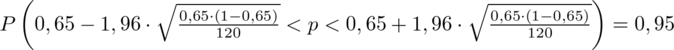
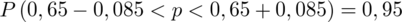
Ad. b)
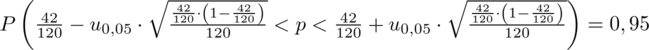
Statystyka
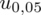 została odczytana w poprzednim podpunkcie:
została odczytana w poprzednim podpunkcie:
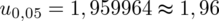 . Uzupełniamy:
. Uzupełniamy:
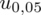 została odczytana w poprzednim podpunkcie:
została odczytana w poprzednim podpunkcie:
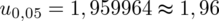 . Uzupełniamy:
. Uzupełniamy: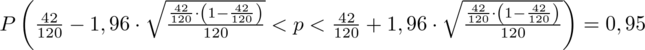
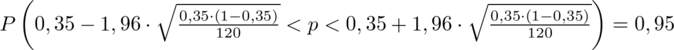
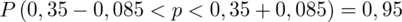
5. WYNIK I INTERPRETACJA.
Ad. a)
Ostatecznie otrzymujemy:
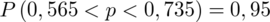
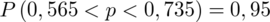
Interpretacja brzmi następująco: Z ufnością 0,95 frakcja osób wypijających do dwóch filiżanek kawy dziennie (włącznie) mieści się w przedziale od 0,565 do 0,735.
Ad. b)
Ostatecznie otrzymujemy:
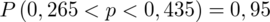
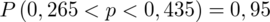
Interpretacja brzmi następująco: Z ufnością 0,95 frakcja osób wypijających co najmniej 3 filiżanki kawy dziennie mieści się w przedziale od 0,265 do 0,435.