
W grupie 3600 losowo wybranych pasażerów warszawskiego metra 1584 osoby stwierdziły, że metro jest dla nich jedynym środkiem dojazdu do pracy.
1. Zbudować przedział ufności dla nieznanej frakcji osób, dla których metro jest jedynym środkiem dojazdu do pracy wśród ogółu pasażerów. Przyjąć współczynnik ufności na poziomie 0,90.
2. Określić przeciętny i maksymalny błąd szacunku.
3. Ocenić, jak zmieni się precyzja oszacowania, jeśli liczebność próby zmniejszymy do 900 osób.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdania:
1. Zbudować przedział ufności dla nieznanej frakcji osób, dla których metro jest jedynym środkiem dojazdu do pracy wśród ogółu pasażerów. Przyjąć współczynnik ufności na poziomie 0,90.
Występują tu zwroty: przedział ufności i współczynnik ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
Zadanie składa się z trzech podpunktów. Każdy z nich zostanie wykonany oddzielnie.
AD. 1.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W grupie 3600 losowo wybranych pasażerów warszawskiego metra 1584 osoby stwierdziły, że metro jest dla nich jedynym środkiem dojazdu do pracy.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wybrania do próby konkretnej ilości osób spośród wszystkich pasażerów warszawskiego metra. Oznaczamy więc liczebność próby
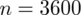 . Uzyskujemy również informację, że 1584 pasażerów spośród 3600 korzysta wyłącznie z metra jako środka transportu do pracy - jest to ilość wyróżnionych obserwacji spośród próby. Oznaczamy ją symbolem
. Uzyskujemy również informację, że 1584 pasażerów spośród 3600 korzysta wyłącznie z metra jako środka transportu do pracy - jest to ilość wyróżnionych obserwacji spośród próby. Oznaczamy ją symbolem
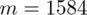 .
.
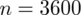 . Uzyskujemy również informację, że 1584 pasażerów spośród 3600 korzysta wyłącznie z metra jako środka transportu do pracy - jest to ilość wyróżnionych obserwacji spośród próby. Oznaczamy ją symbolem
. Uzyskujemy również informację, że 1584 pasażerów spośród 3600 korzysta wyłącznie z metra jako środka transportu do pracy - jest to ilość wyróżnionych obserwacji spośród próby. Oznaczamy ją symbolem
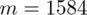 .
.
1. Zbudować przedział ufności dla nieznanej frakcji osób, dla których metro jest jedynym środkiem dojazdu do pracy wśród ogółu pasażerów.
W tym zdaniu nie ma danych liczbowych, więc je pomijamy.
Przyjąć współczynnik ufności na poziomie 0,90.
Podano również współczynnik ufności
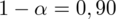 , od razu wyznaczamy
, od razu wyznaczamy
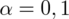 .
.
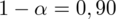 , od razu wyznaczamy
, od razu wyznaczamy
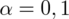 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
pasażerowie warszawskiego metra |
PRÓBA
3600 wybranych pasażerów |
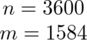
|
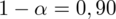 - współczynnik ufności,
- współczynnik ufności,
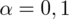
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
1. Zbudować przedział ufności dla nieznanej frakcji osób, dla których metro jest jedynym środkiem dojazdu do pracy wśród ogółu pasażerów.
Słowo frakcja oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
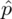 .
.
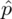 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
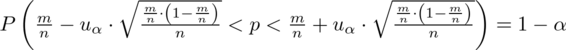 konkretnymi danymi.
konkretnymi danymi.
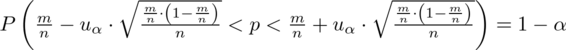 konkretnymi danymi.
konkretnymi danymi.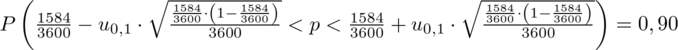
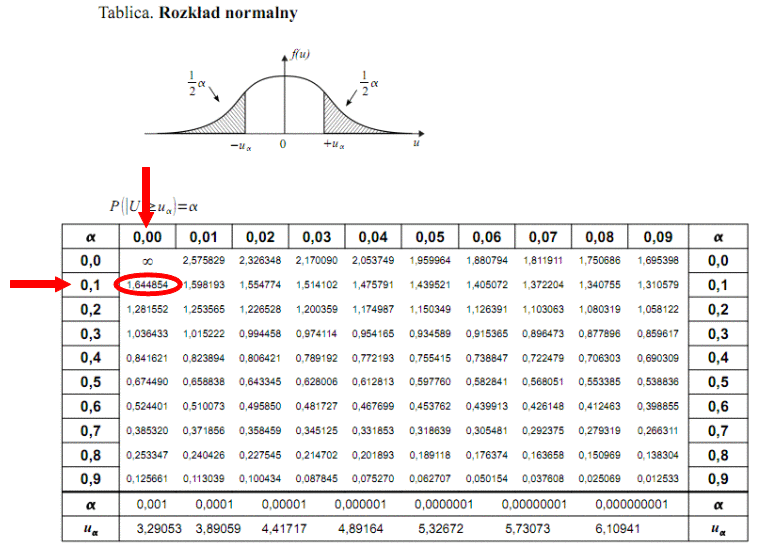
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
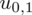 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
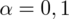 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
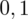 sumujemy
sumujemy
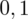 i
i
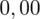 czyli
czyli
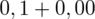 .
.
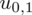 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
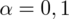 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
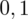 sumujemy
sumujemy
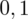 i
i
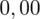 czyli
czyli
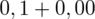 .
.
Wracamy do obliczeń i podstawiamy
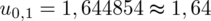 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
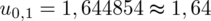 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):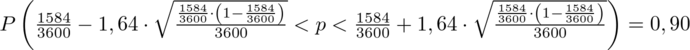
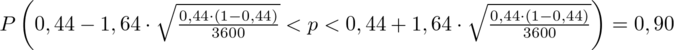
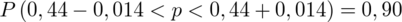
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
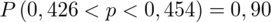
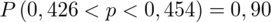
Interpretacja brzmi następująco: Z ufnością 0,90 nieznana frakcja ogółu pasażerów, dla których metro jest jedynym środkiem dojazdu do pracy mieści się w przedziale od 0,426 do 0,454.
AD. 2.
Zacznijmy od określenia maksymalnego błędu szacunku (bezwzględny błąd szacunku)
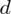 , który jest wielkością odejmowaną i dodawaną do wskaźnika struktury z próby
, który jest wielkością odejmowaną i dodawaną do wskaźnika struktury z próby
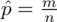 niezależnie od wybranego wzoru. Formuła na
niezależnie od wybranego wzoru. Formuła na
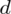 wygląda następująco:
wygląda następująco:
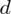 , który jest wielkością odejmowaną i dodawaną do wskaźnika struktury z próby
, który jest wielkością odejmowaną i dodawaną do wskaźnika struktury z próby
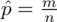 niezależnie od wybranego wzoru. Formuła na
niezależnie od wybranego wzoru. Formuła na
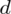 wygląda następująco:
wygląda następująco: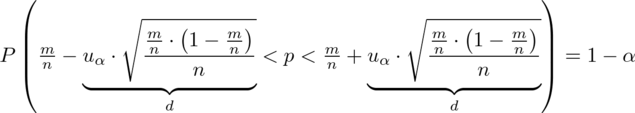
czyli
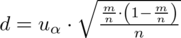 .
.
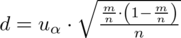 .
.
Wracamy do danych z tabeli w podpunkcie pierwszym i wartości statystyki
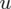 z tablic rozkładu normalnego i uzupełniamy:
z tablic rozkładu normalnego i uzupełniamy:
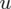 z tablic rozkładu normalnego i uzupełniamy:
z tablic rozkładu normalnego i uzupełniamy: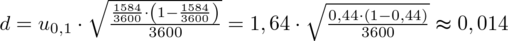
Natomiast przeciętny błąd szacunku jest „okrojoną” wersją wzoru na maksymalny błąd szacunku. Nie bierzemy pod uwagę wartości statystyki odczytanej z odpowiednich tablic, po prostu ją wyrzucamy. Tak więc:
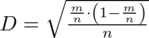 .
.
 .
.
Uzupełniamy wzór konkretnymi liczbami:
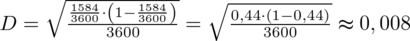
Maksymalny błąd szacunku wynosi 0,014, a przeciętny błąd szacunku 0,008.
AD. 3.
W tym podpunkcie posłużymy się względną precyzją oszacowania, którą w przypadku wskaźnika struktury określamy wzorem
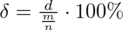 . Na początku obliczymy względną precyzję oszacowania dla pierwotnej treści zadania, tzn. liczebności próby
. Na początku obliczymy względną precyzję oszacowania dla pierwotnej treści zadania, tzn. liczebności próby
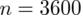 . Wartość
. Wartość
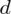 znamy z drugiego podpunktu, zatem ostatecznie otrzymujemy:
znamy z drugiego podpunktu, zatem ostatecznie otrzymujemy:
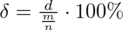 . Na początku obliczymy względną precyzję oszacowania dla pierwotnej treści zadania, tzn. liczebności próby
. Na początku obliczymy względną precyzję oszacowania dla pierwotnej treści zadania, tzn. liczebności próby
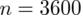 . Wartość
. Wartość
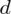 znamy z drugiego podpunktu, zatem ostatecznie otrzymujemy:
znamy z drugiego podpunktu, zatem ostatecznie otrzymujemy: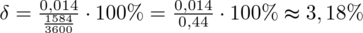
Teraz czas na określenie względnej precyzji szacunku dla liczebności próby
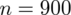 . Zgodnie z założeniami reszta danych pozostaje bez zmian. Istotne jest założenie niezmienności wskaźnika struktury, a więc
. Zgodnie z założeniami reszta danych pozostaje bez zmian. Istotne jest założenie niezmienności wskaźnika struktury, a więc
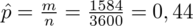 . Tym razem musimy obliczyć wartość
. Tym razem musimy obliczyć wartość
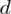 od początku ponownie korzystając ze wzoru
od początku ponownie korzystając ze wzoru
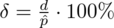 . Obliczamy:
. Obliczamy:
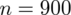 . Zgodnie z założeniami reszta danych pozostaje bez zmian. Istotne jest założenie niezmienności wskaźnika struktury, a więc
. Zgodnie z założeniami reszta danych pozostaje bez zmian. Istotne jest założenie niezmienności wskaźnika struktury, a więc
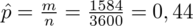 . Tym razem musimy obliczyć wartość
. Tym razem musimy obliczyć wartość
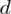 od początku ponownie korzystając ze wzoru
od początku ponownie korzystając ze wzoru
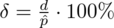 . Obliczamy:
. Obliczamy: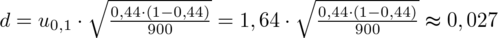
Na koniec względna precyzja szacunku:
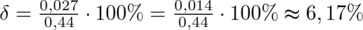
Po zmniejszeniu liczebności próby z 3600 osób do 900 osób względna precyzja oszacowania zmalała o
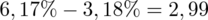 punktu procentowego, czyli prawie dwukrotnie. Coś tu jednak się nie zgadza, prawda? Przecież po zmniejszeniu liczebności próby otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku w tym przypadku spowodowane jest drastycznym zmniejszeniem liczebności próby.
punktu procentowego, czyli prawie dwukrotnie. Coś tu jednak się nie zgadza, prawda? Przecież po zmniejszeniu liczebności próby otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku w tym przypadku spowodowane jest drastycznym zmniejszeniem liczebności próby.
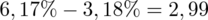 punktu procentowego, czyli prawie dwukrotnie. Coś tu jednak się nie zgadza, prawda? Przecież po zmniejszeniu liczebności próby otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku w tym przypadku spowodowane jest drastycznym zmniejszeniem liczebności próby.
punktu procentowego, czyli prawie dwukrotnie. Coś tu jednak się nie zgadza, prawda? Przecież po zmniejszeniu liczebności próby otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku) jest uprawnione i całkowicie bezpieczne, jeżeli mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku w tym przypadku spowodowane jest drastycznym zmniejszeniem liczebności próby.Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4