
W losowo wybranej próbie 100 studentów SGH 40 osób mieszkało na stałe w Warszawie. Przyjmując współczynnik ufności na poziomie 0,90:
a) oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów,
b) określić, o ile osób należy zwiększyć powyższą próbę, aby dwukrotnie wzrosła precyzja oszacowania.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
a) oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów,
Występuje tu zwrot: oszacować przedziałowo - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. W poprzednim zdaniu Przyjmując współczynnik ufności na poziomie 0,90. dodatkowo znajdujemy wyrażenie współczynnik ufności.
W drugiej części zadania interesuje nas precyzja oszacowania, a pytanie o tą wielkość dotyczy z reguły zadań z estymacji. Do stworzenia wzoru na względną precyzję szacunku potrzebujemy formuły na ten przedział. Będziemy postępować zgodnie ze znanym schematem dotyczącym estymacji przedziałowej i dodatkowo policzymy względną precyzję szacunku. Później zwiększymy dwukrotnie precyzję szacunku i ustalimy o ile należy zwiększyć próbę.
AD. a)
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W losowo wybranej próbie 100 studentów SGH 40 osób mieszkało na stałe w Warszawie.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wybrania do próby konkretnej ilości osób spośród wszystkich studentów SGH. Oznaczamy więc liczebność próby
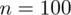 . Uzyskujemy również informację, że 40 studentów spośród 100 mieszka na stale w Warszawie - i byłaby to ilość wyróżnionych obserwacji spośród próby, ale w zdaniu oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów widać, że interesują nas osoby spoza Warszawy. Zatem poza stolicą mieszka
. Uzyskujemy również informację, że 40 studentów spośród 100 mieszka na stale w Warszawie - i byłaby to ilość wyróżnionych obserwacji spośród próby, ale w zdaniu oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów widać, że interesują nas osoby spoza Warszawy. Zatem poza stolicą mieszka
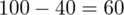 osób. Ilość obserwacji spośród próby wynosi zatem
osób. Ilość obserwacji spośród próby wynosi zatem
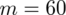 .
.
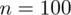 . Uzyskujemy również informację, że 40 studentów spośród 100 mieszka na stale w Warszawie - i byłaby to ilość wyróżnionych obserwacji spośród próby, ale w zdaniu oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów widać, że interesują nas osoby spoza Warszawy. Zatem poza stolicą mieszka
. Uzyskujemy również informację, że 40 studentów spośród 100 mieszka na stale w Warszawie - i byłaby to ilość wyróżnionych obserwacji spośród próby, ale w zdaniu oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów widać, że interesują nas osoby spoza Warszawy. Zatem poza stolicą mieszka
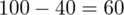 osób. Ilość obserwacji spośród próby wynosi zatem
osób. Ilość obserwacji spośród próby wynosi zatem
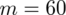 .
.
Przyjmując współczynnik ufności na poziomie 0,90:
Podano również współczynnik ufności
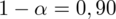 , od razu wyznaczamy
, od razu wyznaczamy
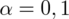 .
.
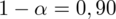 , od razu wyznaczamy
, od razu wyznaczamy
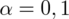 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
studenci SGH |
PRÓBA
100 wybranych studentów |
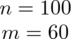

|
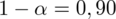 - współczynnik ufności,
- współczynnik ufności,
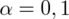
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
a) oszacować przedziałowo udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów,
Słowo udział oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
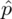 .
.
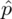 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
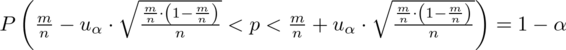 konkretnymi danymi.
konkretnymi danymi.
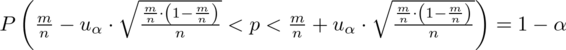 konkretnymi danymi.
konkretnymi danymi.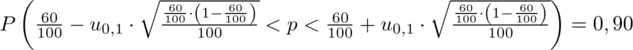
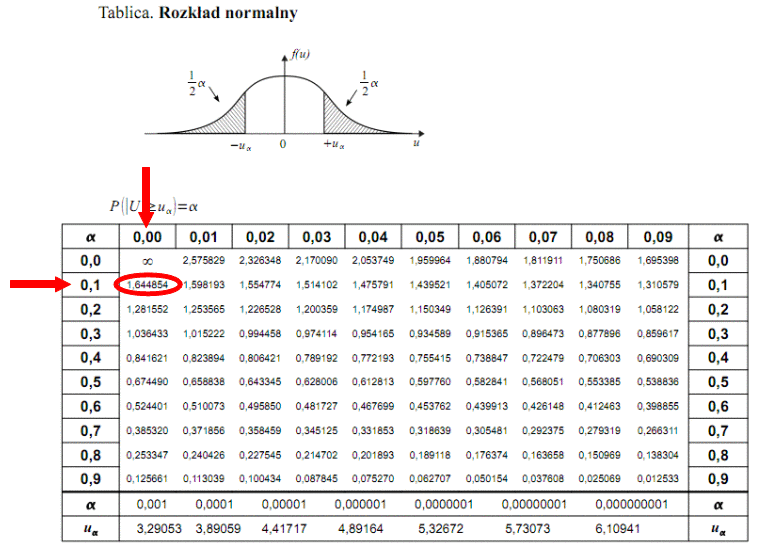
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
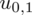 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
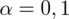 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
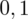 sumujemy
sumujemy
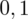 i
i
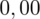 czyli
czyli
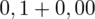 .
.
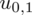 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
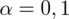 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
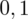 sumujemy
sumujemy
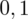 i
i
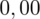 czyli
czyli
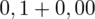 .
.
Wracamy do obliczeń i podstawiamy
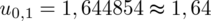 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
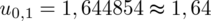 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):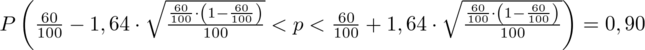
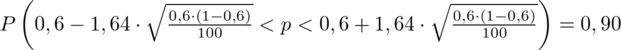
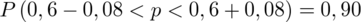
AD. b)
Na początku obliczymy względną precyzję oszacowania
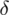 . A więc:
. A więc:
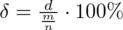 lub
lub
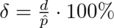 , gdzie
, gdzie
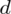 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
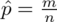 :
:
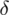 . A więc:
. A więc:
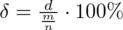 lub
lub
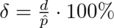 , gdzie
, gdzie
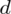 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
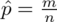 :
: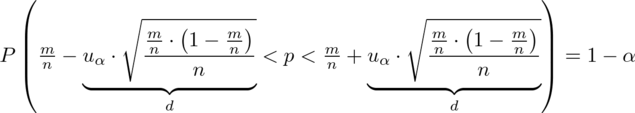
czyli
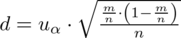 .
.
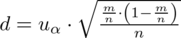 .
.
Formuła na obliczenie
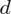 zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
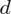 zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
Po wstawieniu danych otrzymujemy:
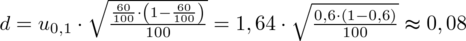
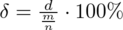
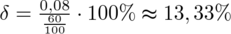
Teraz zgodnie z treścią zadania dwukrotnie zwiększamy precyzję szacunku:
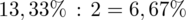
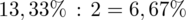
Coś tu jednak się nie zgadza, prawda? Przecież otrzymaliśmy mniejszą liczbę i na chłopski rozum względna precyzja uległa zmniejszeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Tak więc zwiększenie precyzji oszacowania w ujęciu matematycznym polega na zmniejszeniu wartości liczbowej.
Na koniec określimy o ile należy zwiększyć próbę aby precyzja oszacowania wyniosła 6,67%, ponownie skorzystamy ze wzoru na względną precyzję szacunku, ale wprowadzimy zmienną
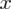 , która będzie oznaczać ilość osób, którą należy dodać do próby. Inne wartości nie ulegają zmianie. Ważne jest założenie niezmienności struktury próby - oznacza to wskaźnik struktury w próbie
, która będzie oznaczać ilość osób, którą należy dodać do próby. Inne wartości nie ulegają zmianie. Ważne jest założenie niezmienności struktury próby - oznacza to wskaźnik struktury w próbie
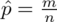 ma pozostać bez zmian, a więc
ma pozostać bez zmian, a więc
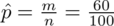 :
:
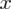 , która będzie oznaczać ilość osób, którą należy dodać do próby. Inne wartości nie ulegają zmianie. Ważne jest założenie niezmienności struktury próby - oznacza to wskaźnik struktury w próbie
, która będzie oznaczać ilość osób, którą należy dodać do próby. Inne wartości nie ulegają zmianie. Ważne jest założenie niezmienności struktury próby - oznacza to wskaźnik struktury w próbie
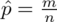 ma pozostać bez zmian, a więc
ma pozostać bez zmian, a więc
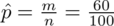 :
: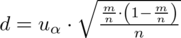 , a potem
, a potem
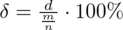
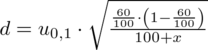
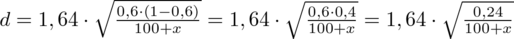
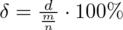

Powstało niezbyt przyjemne równanie i aby je rozwiązać będziemy powoli okrajać ułamek, w którym znajduje się niewiadoma
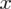 :
:
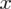 :
: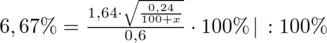
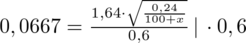
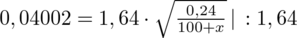
Aby pozbyć się pierwiastka podniesiemy równanie stronami do kwadratu:
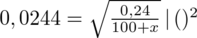
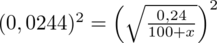
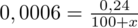
Powstało równanie wymierne, stosujemy dla wygody zapis
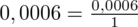 i rozwiązujemy równanie metodą na krzyż:
i rozwiązujemy równanie metodą na krzyż:
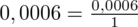 i rozwiązujemy równanie metodą na krzyż:
i rozwiązujemy równanie metodą na krzyż: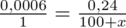
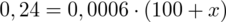
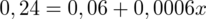
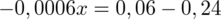
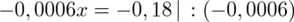
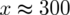
Jak widać podczas procesu rozwiązywania w kolejnych przekształceniach powstawały liczby z dużą ilością miejsc po przecinku. Dla wygody pośrednie wyniki były zaokrąglane. Oczywiście to nie jest jedyny sposób na rozwiązanie tego równania.
5. WYNIK I INTERPRETACJA.
Z podpunktu a) ostatecznie otrzymujemy:
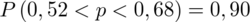
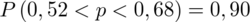
Interpretacja brzmi następująco: Z ufnością 0,90 udział studentów mieszkających na stałe poza Warszawą wśród ogółu studentów mieści się w przedziale od 0,52 do 0,68.
Z podpunktu a) ostatecznie otrzymujemy: Aby dwukrotnie wzrosła precyzja oszacowania należy dolosować do próby około 300 osób.
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4