
W losowo wybranej próbie 200 studentów pewnej uczelni 70 osób wydaje miesięcznie na gazety i czasopisma ponad 10 zł.
a) Wyznaczyć przedział ufności dla odsetka studentów, którzy wydają miesięcznie na ten cel co najwyżej 10 zł na poziomie ufności
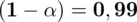 . Jaka jest dokładność oszacowania?
. Jaka jest dokładność oszacowania?
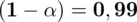 . Jaka jest dokładność oszacowania?
. Jaka jest dokładność oszacowania?
b) Jak zmieni się długość przedziału ufności, gdy poziom ufności
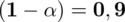 ?
?
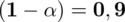 ?
?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Wyznaczyć przedział ufności dla odsetka studentów, którzy wydają miesięcznie na ten cel co najwyżej 10 zł na poziomie ufności
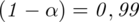 .
.
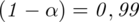 .
.
Występują tu zwroty: przedział ufności i poziom ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. W ostatnim zdaniu (podpunkt b) również odnajdziemy obydwa wyrażenia.
Dodatkowo w pierwszej części zadania interesuje nas dokładność oszacowania, a pytanie o tą wielkość dotyczy z reguły zadań z estymacji. Dokładność oszacowania zbadamy obliczając względny błąd szacunku. Do stworzenia wzoru na względną precyzję szacunku potrzebujemy formuły na przedział ufności. Będziemy postępować zgodnie ze znanym schematem dotyczącym estymacji przedziałowej i dodatkowo policzymy względny błąd losowy zwany inaczej względną precyzją szacunku. W drugiej części zadania stworzymy przedział ufności, tylko przyjmiemy inny współczynnik ufności i porównamy wyniki.
AD. a)
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W losowo wybranej próbie 200 studentów pewnej uczelni 70 osób wydaje miesięcznie na gazety i czasopisma ponad 10 zł.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wybrania do próby konkretnej ilości osób spośród wszystkich studentów pewnej uczelni. Oznaczamy więc liczebność próby
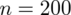 . Uzyskujemy również informację, że 70 studentów spośród 200 wydaje miesięcznie na prasę ponad 10 zł - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Uzyskujemy również informację, że 70 studentów spośród 200 wydaje miesięcznie na prasę ponad 10 zł - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
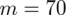 .
.
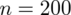 . Uzyskujemy również informację, że 70 studentów spośród 200 wydaje miesięcznie na prasę ponad 10 zł - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Uzyskujemy również informację, że 70 studentów spośród 200 wydaje miesięcznie na prasę ponad 10 zł - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
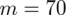 .
.
Wyznaczyć przedział ufności dla odsetka studentów, którzy wydają miesięcznie na ten cel co najwyżej 10 zł na poziomie ufności
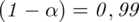 .
.
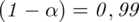 .
.
Podano również współczynnik ufności
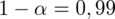 , od razu wyznaczamy
, od razu wyznaczamy
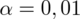 .
.
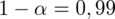 , od razu wyznaczamy
, od razu wyznaczamy
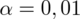 .
.
Jaka jest dokładność oszacowania?
W tym zdaniu nie ma danych liczbowych, więc je pomijamy.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
studenci pewnej uczelni |
PRÓBA
200 wybranych studentów |
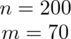

|
 - współczynnik ufności,
- współczynnik ufności,
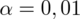
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
Wyznaczyć przedział ufności dla odsetka studentów, którzy wydają miesięcznie na ten cel co najwyżej 10 zł na poziomie ufności
 .
.
 .
.
Słowo odsetek oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
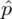 .
.
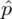 .
.
Nadszedł czas by określić wzór na względną precyzję oszacowania wskaźnika struktury
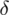 .
.
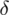 .
.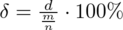 lub
lub
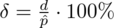 , gdzie
, gdzie
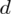 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
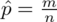 :
:
czyli
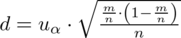 .
.
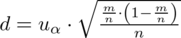 .
.
Formuła na obliczenie
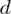 zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
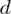 zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zawsze zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
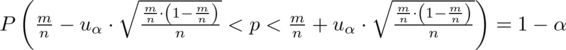 konkretnymi danymi.
konkretnymi danymi.
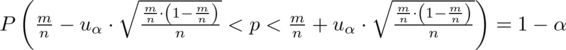 konkretnymi danymi.
konkretnymi danymi.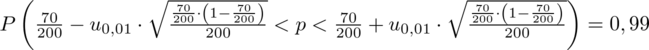
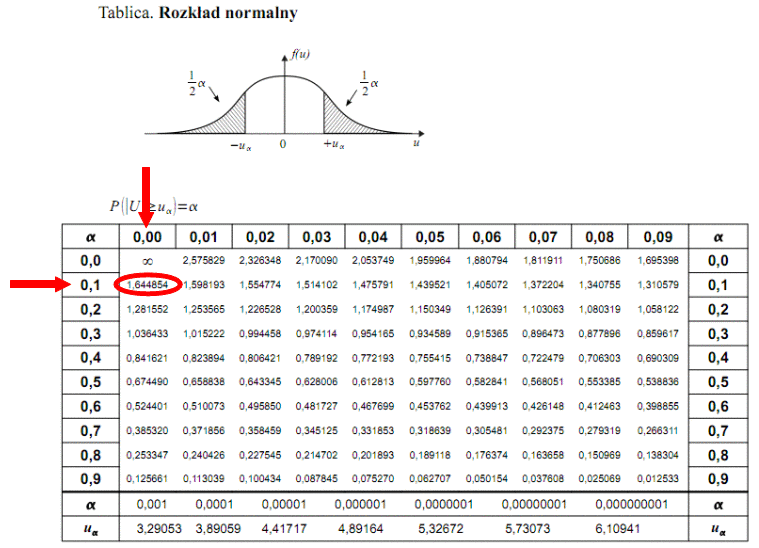
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
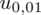 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
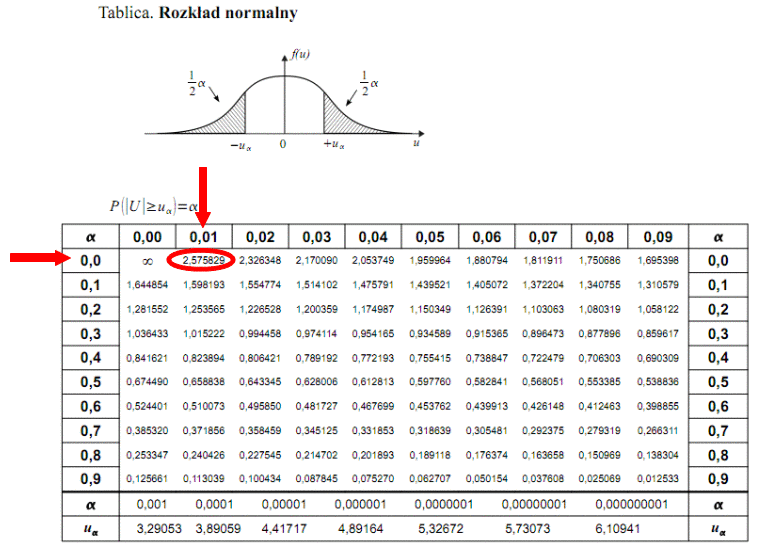
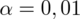 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
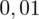 sumujemy
sumujemy
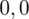 i
i
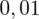 czyli
czyli
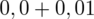 .
.
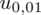 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
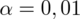 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
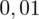 sumujemy
sumujemy
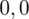 i
i
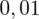 czyli
czyli
 .
.
Wracamy do obliczeń i podstawiamy
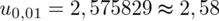 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
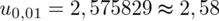 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):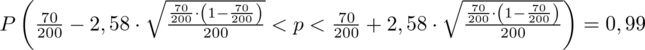
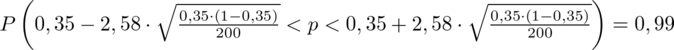
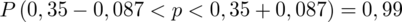
Z kolei względna precyzja szacunku:
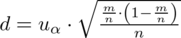
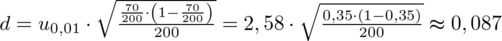
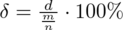
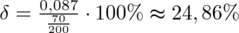
AD. b)
W tym podpunkcie zmienia się tylko współczynnik ufności
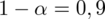 (
(
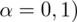 , szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
, szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
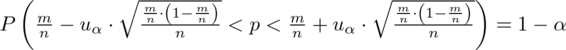 .
.
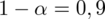 (
(
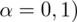 , szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
, szacujemy ponownie wskaźnik struktury, a więc wzór na przedział ufności pozostaje bez zmian:
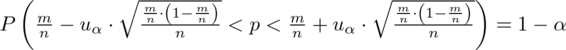 .
.
Uzupełniamy zatem wzór zmieniając jedynie
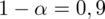 (
(
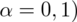 :
:
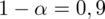 (
(
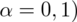 :
: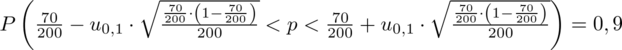
Ponownie odczytujemy odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
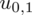 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
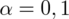 . Sumujemy wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Sumujemy wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
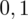 sumujemy
sumujemy
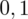 i
i
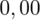 czyli
czyli
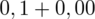 .
.
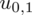 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
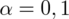 . Sumujemy wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Sumujemy wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
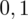 sumujemy
sumujemy
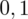 i
i
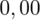 czyli
czyli
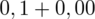 .
.
Wracamy do obliczeń i podstawiamy
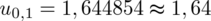 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
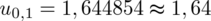 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):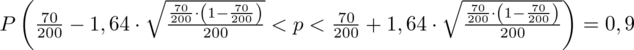
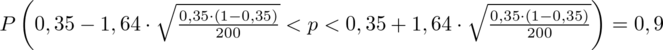

5. WYNIK I INTERPRETACJA.
Z podpunktu a) ostatecznie otrzymujemy:
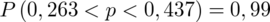
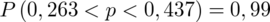
Interpretacja brzmi następująco: Z ufnością 0,99 odsetek studentów, którzy wydają miesięcznie na gazety i czasopisma co najwyżej 10 zł mieści się w przedziale od 0,263 do 0,437. Względna precyzja szacunku wynosząca 24,86% przekracza 10%, a więc wnioskowanie jest niebezpieczne i należy je niezwłocznie przerwać.
Z podpunktu b) ostatecznie otrzymujemy:
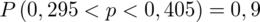
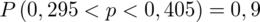
Interpretacja brzmi następująco: Z ufnością 0,9 odsetek studentów, którzy wydają miesięcznie na gazety i czasopisma co najwyżej 10 zł mieści się w przedziale od 0,295 do 0,405.
Porównując otrzymane wyniki można stwierdzić, że po zmniejszeniu współczynnika ufności z 0,99 do 0,9 długość przedziału ufności uległa zmniejszeniu. Wizualnie można to przedstawić w taki sposób:
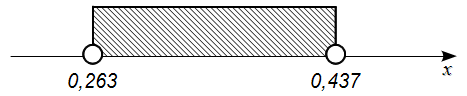
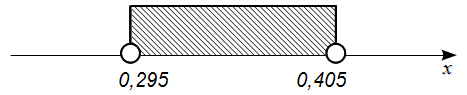
Prawdopodobieństwo trafienia w odpowiedni wynik przy szacowaniu odsetka jest większa przy 0,99 (bo mamy dłuższy przedział), ale dokładność szacunku się zmniejsza, ponieważ zakres w który będziemy trafiać jest znacznie dłuższy, więc można bardziej się pomylić. Na chłopski rozum: wyobraźmy sobie dwie tarcze strzeleckie. Jedna z nich (krótszy przedział) to środek tarczy stanowiący czarny obszar z dziesiątką, a druga (dłuższy przedział) to normalna tarcza strzelecka również z białymi polami. Prawdopodobieństwo jakiegokolwiek trafienia jest wyższe w przypadku drugiej tarczy, bo jest większa, ale już dokładność strzału w przypadku trafienia (jeśli za cel postawimy 10) jest wyższe w przypadku małej tarczy, bo jeśli w nią trafimy to strzał w czarne pole jest bliżej 10 niż np. strzał w białe pole dużej tarczy.
Zadanie pochodzi z: Statystyka : elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka. Wyd. 6 popr., Wrocław : Wydawnictwo Akademii Ekonomicznej, 2006. - 455 s.: il.; 24 cm. ISBN 83-7011-783-X