
Wylosowano 300 mieszkańców pewnego miasta. 200 spośród nich było wyposażonych w telefon. Co można sądzić o odsetku mieszkańców wyposażonych w telefon? Współczynnik ufności wynosi 0,90. Ile wynosi poziom precyzji względnej?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
W tym zadaniu nie ma słowa, które jednoznacznie wskazywałoby, że jest to zadanie dotyczące estymacji przedziałowej.
„Co można sądzić o odsetku mieszkańców wyposażonych w telefon? Współczynnik ufności wynosi 0,90.”
Co prawda występuje wyrażenie współczynnik ufności, ale to trochę za mało. Bardziej naprowadzają nas na właściwy trop słowa: co można sądzić o odsetku, ponieważ oznacza to, że odsetek należy oszacować przedziałem ufności. Bardzo rzadko stosuje się tzw. estymację punktową (czyli jedna konkretna liczba), ponieważ prawdopodobieństwo właściwego wyniku jest praktycznie równe zero. Poza tym interesuje nas poziom względnej precyzji szacunku, a pytanie o tą wielkość dotyczy z reguły zadań z estymacji. W zadaniu interesuje nas przedział ufności, a do podania wzoru na względną precyzję szacunku potrzebujemy formuły na ten przedział. Będziemy postępować zgodnie ze znanym schematem dotyczącym estymacji przedziałowej i dodatkowo policzymy względną precyzję szacunku.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
Wylosowano 300 mieszkańców pewnego miasta.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wybrania do próby konkretnej ilości osób spośród wszystkich mieszkańców pewnego miasta. Oznaczamy więc liczebność próby
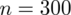 .
.
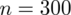 .
.
200 spośród nich było wyposażonych w telefon.
Uzyskujemy informację, że 200 mieszkańców spośród 300 posiada telefon - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
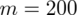 .
.
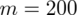 .
.
Co można sądzić o odsetku mieszkańców wyposażonych w telefon?
W tym zdaniu nie ma danych liczbowych, więc je pomijamy.
Współczynnik ufności wynosi 0,90.
Podano również współczynnik ufności
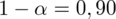 , od razu wyznaczamy
, od razu wyznaczamy
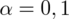 .
.
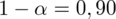 , od razu wyznaczamy
, od razu wyznaczamy
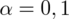 .
.
Ile wynosi poziom precyzji względnej?
Tu też nie ma danych liczbowych.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
mieszkańcy pewnego miasta |
PRÓBA
300 wybranych mieszkańców |
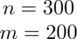

|
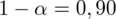 - współczynnik ufności,
- współczynnik ufności,
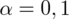
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
Co można sądzić o odsetku mieszkańców wyposażonych w telefon?
Słowo odsetek oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
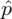 .
.
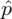 .
.
Nadszedł czas by określić wzór na względną precyzję oszacowania wskaźnika struktury
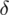 .
.
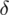 .
.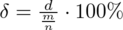 lub
lub
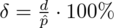 , gdzie
, gdzie
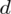 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną wskaźnika struktury z próby
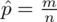 :
: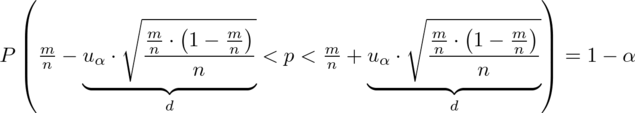
czyli
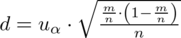 .
.
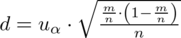 .
.
Powtarzam jeszcze raz, że formuła na obliczenie
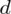 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
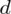 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do wskaźnika struktury z próby.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
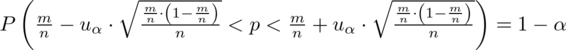 konkretnymi danymi.
konkretnymi danymi.
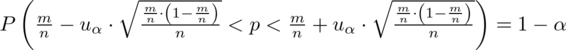 konkretnymi danymi.
konkretnymi danymi.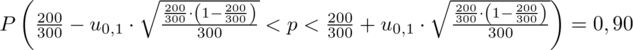
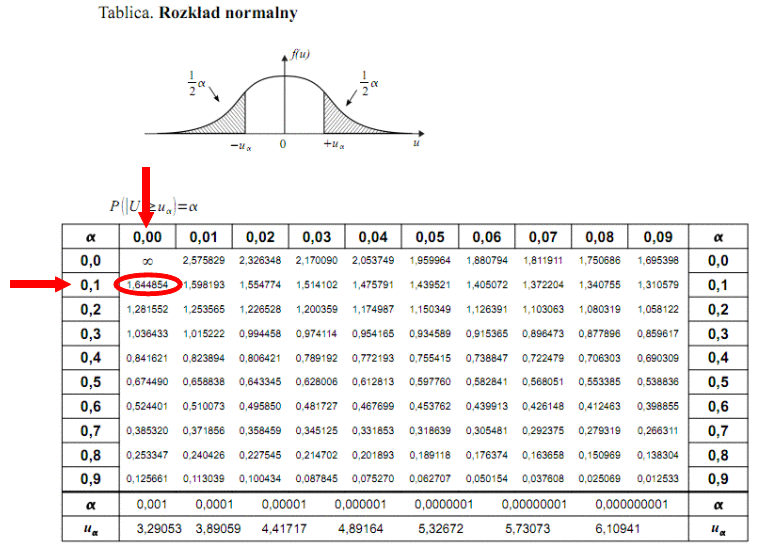
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
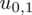 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
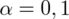 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
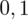 sumujemy
sumujemy
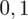 i
i
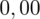 czyli
czyli
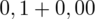 .
.
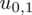 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
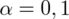 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
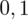 sumujemy
sumujemy
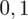 i
i
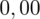 czyli
czyli
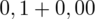 .
.
Wracamy do obliczeń i podstawiamy
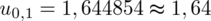 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
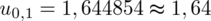 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):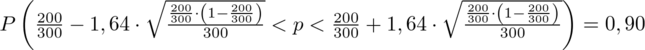
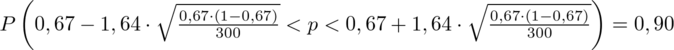
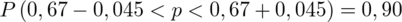
Z kolei względna precyzja szacunku:
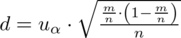
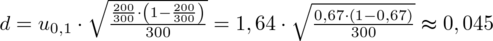
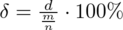
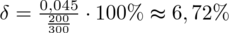
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
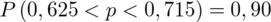
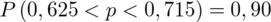
Interpretacja brzmi następująco: Z ufnością 0,90 odsetek ogółu mieszkańców miasta wyposażonych w telefon mieści się w przedziale od 0,625 do 0,715. Względna precyzja szacunku wynosząca 6,72% mieści się od 5% do 10%, a więc wnioskowanie jest możliwe, ale z zalecaną ostrożnością.