
W losowej próbie 1217 dorosłych Polaków postawiono pytanie ”Czy premiera powinien zastąpić inny polityk?”. Odsetek odpowiedzi „tak” w całej populacji oszacowano przedziałem ufności i uzyskano wynik
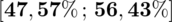 . Jaki był odsetek odpowiedzi „tak” w próbie?
. Jaki był odsetek odpowiedzi „tak” w próbie?
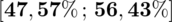 . Jaki był odsetek odpowiedzi „tak” w próbie?
. Jaki był odsetek odpowiedzi „tak” w próbie?
a) nie można określić, gdyż nie podano współczynnika ufności, przy którym zbudowano przedział;
b) nie można określić, gdyż nie podano liczby odpowiedzi „tak” w próbie;
c) 49%;
d) 52%;
e) inny wniosek, jaki?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Odsetek odpowiedzi „tak” w całej populacji oszacowano przedziałem ufności i uzyskano wynik
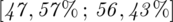 .
.
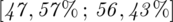 .
.
Występuje tu zwrot: oszacowano przedziałem ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. W jednym z wariantów odpowiedzi nie można określić, gdyż nie podano współczynnika ufności, przy którym zbudowano przedział; znajdujemy dodatkowo wyrażenie: współczynnik ufności.
Podano końcówki przedziału ufności
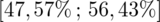 , a szukany jest odsetek odpowiedzi na tak z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
, a szukany jest odsetek odpowiedzi na tak z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
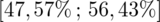 , a szukany jest odsetek odpowiedzi na tak z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
, a szukany jest odsetek odpowiedzi na tak z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W losowej próbie 1217 dorosłych Polaków postawiono pytanie ”Czy premiera powinien zastąpić inny polityk?
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości osób spośród Polaków. Oznaczamy więc liczebność próby
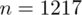 .
.
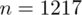 .
.
Odsetek odpowiedzi „tak” w całej populacji oszacowano przedziałem ufności i uzyskano wynik
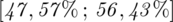 .
.
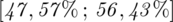 .
.
Podano również przedział ufności. Wiemy, że odsetek odpowiedzi na tak mieści się w przedziale od 47,57% do 56,43%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
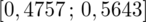 .
.
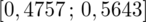 .
.
Jaki był odsetek odpowiedzi „tak” w próbie?
Naszą niewiadomą jest odsetek obserwacji w próbie, który oznacza się symbolem
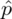 .
.
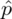 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
dorośli Polacy |
PRÓBA
1217 wybranych Polaków |
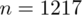
|
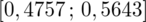 - końcówki przedziału ufności dla odsetka z populacji
- końcówki przedziału ufności dla odsetka z populacji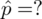 - odsetek obserwacji w próbie
- odsetek obserwacji w próbie
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który został oszacowany przedziałem ufności i wyłapujemy słowo:
Odsetek odpowiedzi „tak” w całej populacji oszacowano przedziałem ufności i uzyskano wynik
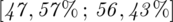 .
.
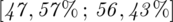 .
.
Słowo odsetek oznacza, że będziemy zbudowano przedział ufności dla wskaźnika struktury p z populacji. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy do wyboru dwie formuły. Szukamy
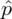 , dlatego użyjemy drugiego wzoru.
, dlatego użyjemy drugiego wzoru.
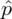 , dlatego użyjemy drugiego wzoru.
, dlatego użyjemy drugiego wzoru. 
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
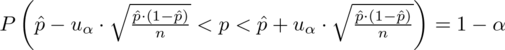 konkretnymi liczbami.
konkretnymi liczbami.
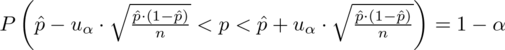 konkretnymi liczbami.
konkretnymi liczbami.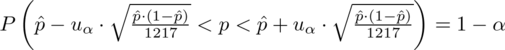
Jak widać, niewiele zostało wpisane, ponieważ oprócz szukanego parametru
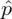 nie możemy uzupełnić współczynnika ufności
nie możemy uzupełnić współczynnika ufności
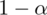 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
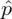 nie możemy uzupełnić współczynnika ufności
nie możemy uzupełnić współczynnika ufności
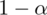 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.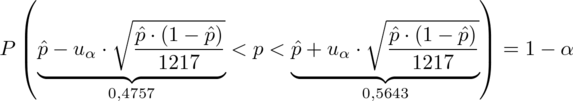
Nie znamy wartości
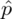 i
i
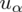 , więc potraktujmy te parametry jako niewiadome i rozwiążemy układ równań aby je wyznaczyć. Wykorzystamy podane końcówki przedziału ufności. Dlaczego układ równań? Do wyznaczenia jednej niewiadomej wystarczy jedno równanie, do wyznaczenia dwóch niewiadomych potrzebujemy układu dwóch równań. Wobec tego otrzymujemy:
, więc potraktujmy te parametry jako niewiadome i rozwiążemy układ równań aby je wyznaczyć. Wykorzystamy podane końcówki przedziału ufności. Dlaczego układ równań? Do wyznaczenia jednej niewiadomej wystarczy jedno równanie, do wyznaczenia dwóch niewiadomych potrzebujemy układu dwóch równań. Wobec tego otrzymujemy:
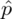 i
i
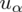 , więc potraktujmy te parametry jako niewiadome i rozwiążemy układ równań aby je wyznaczyć. Wykorzystamy podane końcówki przedziału ufności. Dlaczego układ równań? Do wyznaczenia jednej niewiadomej wystarczy jedno równanie, do wyznaczenia dwóch niewiadomych potrzebujemy układu dwóch równań. Wobec tego otrzymujemy:
, więc potraktujmy te parametry jako niewiadome i rozwiążemy układ równań aby je wyznaczyć. Wykorzystamy podane końcówki przedziału ufności. Dlaczego układ równań? Do wyznaczenia jednej niewiadomej wystarczy jedno równanie, do wyznaczenia dwóch niewiadomych potrzebujemy układu dwóch równań. Wobec tego otrzymujemy: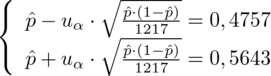
Sam układ nie wygląda zbyt zachęcająco, ponieważ pojawiają się w nim pierwiastki, ale zauważmy, że wyrażenie
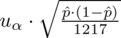 znajduje się w obu równaniach z przeciwnymi znakami. Jest to wymarzona sytuacja z punktu widzenia rozwiązywania układu równań za pomocą metody przeciwnych współczynników, ponieważ po dodaniu stronami obu równań wyrażenie to po prostu zredukuje się do zera i zniknie, a więc:
znajduje się w obu równaniach z przeciwnymi znakami. Jest to wymarzona sytuacja z punktu widzenia rozwiązywania układu równań za pomocą metody przeciwnych współczynników, ponieważ po dodaniu stronami obu równań wyrażenie to po prostu zredukuje się do zera i zniknie, a więc:
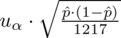 znajduje się w obu równaniach z przeciwnymi znakami. Jest to wymarzona sytuacja z punktu widzenia rozwiązywania układu równań za pomocą metody przeciwnych współczynników, ponieważ po dodaniu stronami obu równań wyrażenie to po prostu zredukuje się do zera i zniknie, a więc:
znajduje się w obu równaniach z przeciwnymi znakami. Jest to wymarzona sytuacja z punktu widzenia rozwiązywania układu równań za pomocą metody przeciwnych współczynników, ponieważ po dodaniu stronami obu równań wyrażenie to po prostu zredukuje się do zera i zniknie, a więc: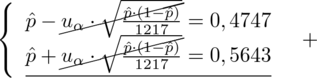
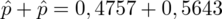
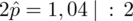
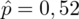
Oczywiście możemy już obliczyć wartość
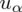 , ale nie będziemy tego robić, ponieważ pytano nas tylko o wartość
, ale nie będziemy tego robić, ponieważ pytano nas tylko o wartość
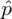 . Jak widać tablice rozkładu normalnego w tym zadaniu są zbędne, ponieważ nie interesuje nas wartość współczynnika ufności.
. Jak widać tablice rozkładu normalnego w tym zadaniu są zbędne, ponieważ nie interesuje nas wartość współczynnika ufności.
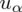 , ale nie będziemy tego robić, ponieważ pytano nas tylko o wartość
, ale nie będziemy tego robić, ponieważ pytano nas tylko o wartość
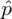 . Jak widać tablice rozkładu normalnego w tym zadaniu są zbędne, ponieważ nie interesuje nas wartość współczynnika ufności.
. Jak widać tablice rozkładu normalnego w tym zadaniu są zbędne, ponieważ nie interesuje nas wartość współczynnika ufności.
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy odsetek obserwacji w próbie dotyczący odpowiedzi na tak równy
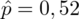 . Po zamianie na procenty (mnożenie przez 100) otrzymujemy
. Po zamianie na procenty (mnożenie przez 100) otrzymujemy
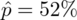 , a więc prawidłowa jest odpowiedź D.
, a więc prawidłowa jest odpowiedź D.
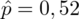 . Po zamianie na procenty (mnożenie przez 100) otrzymujemy
. Po zamianie na procenty (mnożenie przez 100) otrzymujemy
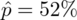 , a więc prawidłowa jest odpowiedź D.
, a więc prawidłowa jest odpowiedź D.
Interpretacja przedziału ufności nie jest w tym zadaniu potrzebna.