
W wyniku kontroli jakości losowo wybranych urządzeń elektrotechnicznych produkowanych przez jeden z zakładów tej branży stwierdzono, że 6 urządzeń miało usterki techniczne. Przedziałowe oszacowanie odsetka urządzeń wadliwych w całej wyprodukowanej partii urządzeń, przy współczynniku ufności równym 0,9545, dało wynik: (0,3%; 2,7%). Ile sztuk wyrobów pobrano do próby w celu oszacowania odsetka ogółu urządzeń wadliwych?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Przedziałowe oszacowanie odsetka urządzeń wadliwych w całej wyprodukowanej partii urządzeń, przy współczynniku ufności równym 0,9545, dało wynik: (0,3%; 2,7%).
Występuje tu zwroty: przedziałowe oszacowanie oraz współczynnik ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. Określono również sam przedział.
Podano końcówki przedziału ufności (0,3%; 2,7%), a niewiadomą stanowi liczebność próby z reguły występująca w danych, wobec tego określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W wyniku kontroli jakości losowo wybranych urządzeń elektrotechnicznych produkowanych przez jeden z zakładów tej branży stwierdzono, że 6 urządzeń miało usterki techniczne.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat kontroli losowo wybranych urządzeń spośród wszystkich maszyn z jednego zakładu. Samej liczebności próby nie podano, ale uzyskujemy informację, że 6 urządzeń spośród badanych ma problemy techniczne - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
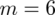 .
.
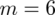 .
.
Przedziałowe oszacowanie odsetka urządzeń wadliwych w całej wyprodukowanej partii urządzeń, przy współczynniku ufności równym 0,9545, dało wynik: (0,3%; 2,7%).
Poznajemy wartość współczynnika ufności
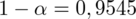 , od razu wyznaczamy
, od razu wyznaczamy
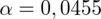 . Podano również przedział ufności. Wiemy, że odsetek urządzeń wadliwych mieści się w przedziale od 0,3% do 2,7%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
. Podano również przedział ufności. Wiemy, że odsetek urządzeń wadliwych mieści się w przedziale od 0,3% do 2,7%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
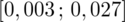 .
.
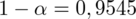 , od razu wyznaczamy
, od razu wyznaczamy
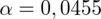 . Podano również przedział ufności. Wiemy, że odsetek urządzeń wadliwych mieści się w przedziale od 0,3% do 2,7%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
. Podano również przedział ufności. Wiemy, że odsetek urządzeń wadliwych mieści się w przedziale od 0,3% do 2,7%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
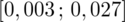 .
.
Ile sztuk wyrobów pobrano do próby w celu oszacowania odsetka ogółu urządzeń wadliwych?
Naszą niewiadomą jest liczebność próby, a więc
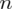 .
.
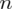 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
urządzenia elektrotechniczne produkowane przez dany zakład |
PRÓBA
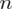 wybranych urządzeń
wybranych urządzeń |
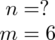
|
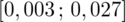 - końcówki przedziału ufności dla odsetka z populacji
- końcówki przedziału ufności dla odsetka z populacji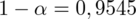 - współczynnik ufności,
- współczynnik ufności,
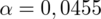
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w przedostatnim zdaniu wyłapujemy słowo:
Przedziałowe oszacowanie odsetka urządzeń wadliwych w całej wyprodukowanej partii urządzeń, przy współczynniku ufności równym 0,9545, dało wynik: (0,3%; 2,7%).
Słowo odsetek oznacza, że przedział ufności zbudowano dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
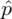 .
.
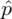 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
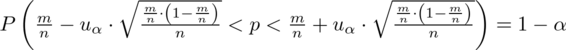 konkretnymi danymi.
konkretnymi danymi.
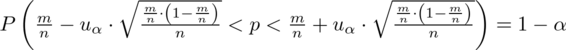 konkretnymi danymi.
konkretnymi danymi.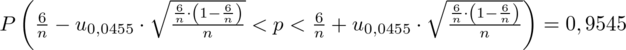
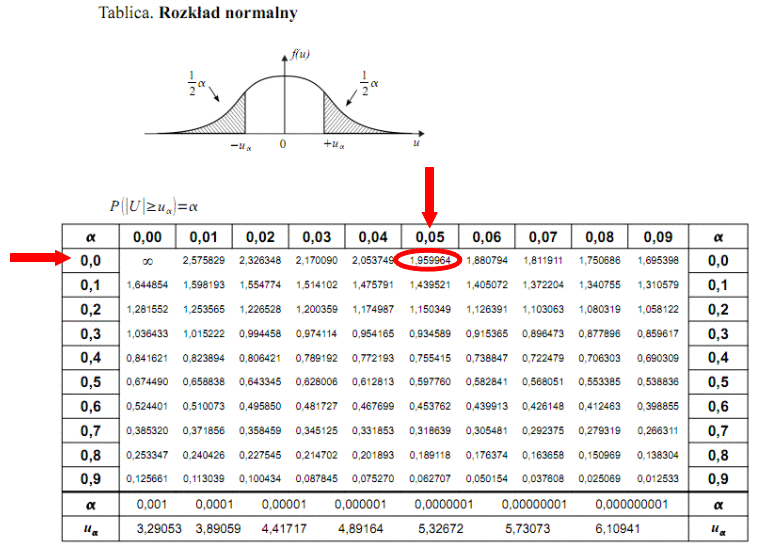
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
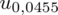 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
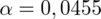 . Niestety, z reguły rzadko dysponujemy aż tak dokładnymi tablicami rozkładu normalnego, więc przyjmiemy najbliższą wartość
. Niestety, z reguły rzadko dysponujemy aż tak dokładnymi tablicami rozkładu normalnego, więc przyjmiemy najbliższą wartość
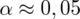 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
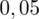 sumujemy
sumujemy
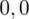 i
i
 czyli
czyli
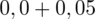 .
.
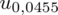 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
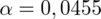 . Niestety, z reguły rzadko dysponujemy aż tak dokładnymi tablicami rozkładu normalnego, więc przyjmiemy najbliższą wartość
. Niestety, z reguły rzadko dysponujemy aż tak dokładnymi tablicami rozkładu normalnego, więc przyjmiemy najbliższą wartość
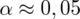 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
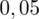 sumujemy
sumujemy
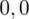 i
i
 czyli
czyli
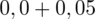 .
.
Wracamy do obliczeń i podstawiamy
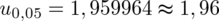 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
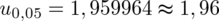 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)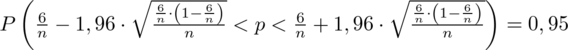
Jak widać, nie możemy uzupełnić liczebności próby oznaczonej jako
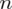 i tym samym doprowadzić obliczeń do końca. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
i tym samym doprowadzić obliczeń do końca. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
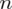 i tym samym doprowadzić obliczeń do końca. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
i tym samym doprowadzić obliczeń do końca. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.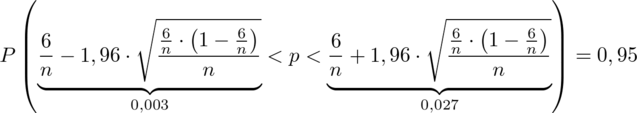
Nie znamy wartości
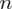 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,003 czy 0,027? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,003 czy 0,027? Jest to całkowicie obojętne, ponieważ w obu przypadkach
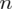 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
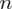 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,003 czy 0,027? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,003 czy 0,027? Jest to całkowicie obojętne, ponieważ w obu przypadkach
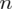 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład: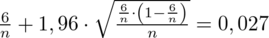
Powyższe równanie zawiera tylko jedną niewiadomą, ale z matematycznego punktu widzenia nie należy do najprzyjemniej rozwiązujących się równań (pierwiastek praktycznie zawsze komplikuje sprawę). Oczywiście można się pomęczyć lub wpisać je do dowolnego programu komputerowego rozwiązującego właściwie każde równanie, ale w tym przypadku istnieje możliwość obejścia problemu, ponieważ dysponujemy (jak już wcześniej wspomniałam) drugą końcówką przedziału ufności, a więc:

Na pierwszy rzut oka te drugie równanie nie zmienia naszej sytuacji, bo jest prawie identyczne mając na uwadze sposób rozwiązywania, ale łącząc te dwa równania i dodając je stronami otrzymujemy zapis:
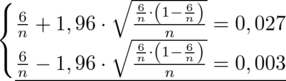 +
+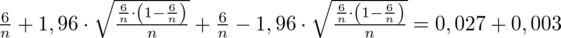
Teraz dokładniej przyjrzyjmy się się powstałemu równaniu. Wydaje się bardziej skomplikowane niż dwa poprzednie, ale brzydkie wyrażenie z pierwiastkiem elegancko się skraca:
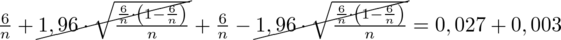
Otrzymujemy banalne równanie:
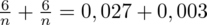
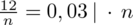
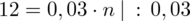

5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy liczebność próby
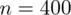 .
.
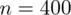 .
.
Interpretacja przedziału ufności nie jest potrzebna, ponieważ pytano nas o liczebność próby.
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4