
W 100-osobowej losowo wybranej próbie studentów 36 mieszkało na stale w Białymstoku. Przedział ufności wyznaczony dla odsetka ogółu studentów mieszkających w Białymstoku ma postać
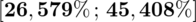 . Przy jakim współczynniku ufności wyznaczano ten przedział?
. Przy jakim współczynniku ufności wyznaczano ten przedział?
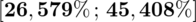 . Przy jakim współczynniku ufności wyznaczano ten przedział?
. Przy jakim współczynniku ufności wyznaczano ten przedział?
a) 0,98 b) 0,95 c) 0,99 d) 0,90
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Przedział ufności wyznaczony dla odsetka ogółu studentów mieszkających w Białymstoku ma postać
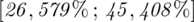 .
.
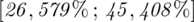 .
.
Występuje tu zwrot: przedział ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej. W kolejnym zdaniu Przy jakim współczynniku ufności wyznaczano ten przedział? znajdujemy dodatkowo wyrażenie: współczynnik ufności.
Podano końcówki przedziału ufności
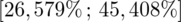 , a szukany jest współczynnik ufności z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
, a szukany jest współczynnik ufności z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
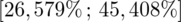 , a szukany jest współczynnik ufności z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
, a szukany jest współczynnik ufności z reguły występujący w danych, z tego względu określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W 100-osobowej losowo wybranej próbie studentów 36 mieszkało na stale w Białymstoku.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości osób spośród studentów. Oznaczamy więc liczebność próby
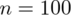 . Ponadto uzyskujemy informację, że 36 osób spośród 100 mieszka na stałe w Białymstoku - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Ponadto uzyskujemy informację, że 36 osób spośród 100 mieszka na stałe w Białymstoku - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
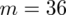 .
.
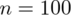 . Ponadto uzyskujemy informację, że 36 osób spośród 100 mieszka na stałe w Białymstoku - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Ponadto uzyskujemy informację, że 36 osób spośród 100 mieszka na stałe w Białymstoku - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
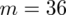 .
.
Przedział ufności wyznaczony dla odsetka ogółu studentów mieszkających w Białymstoku ma postać
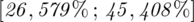 .
.
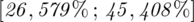 .
.
Podano również przedział ufności. Wiemy, że odsetek populacji studentów mieszkających w Białymstoku mieści się w przedziale od 26,579% do 45,408%. Od razu przeliczmy końcówki przedziału ufności z procentów na ułamki (dzielimy przez 100), a więc
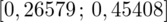 .
.
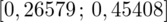 .
.
Przy jakim współczynniku ufności wyznaczano ten przedział?
Naszą niewiadomą jest współczynnik ufności
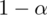 .
.
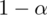 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
studenci |
PRÓBA
100 wybranych studentów |
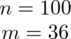
|
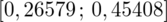 - końcówki przedziału ufności dla odsetka z populacji
- końcówki przedziału ufności dla odsetka z populacji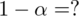 - współczynnik ufności,
- współczynnik ufności,
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w przedostatnim zdaniu wyłapujemy słowo:
Przedział ufności wyznaczony dla odsetka ogółu studentów mieszkających w Białymstoku ma postać
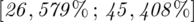 .
.
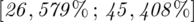 .
.
Słowo odsetek oznacza, że przedział ufności zbudowano dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
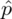 .
.
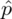 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
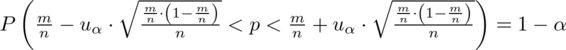 konkretnymi danymi.
konkretnymi danymi.
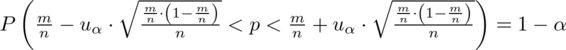 konkretnymi danymi.
konkretnymi danymi.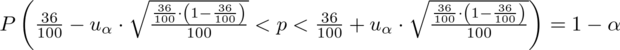
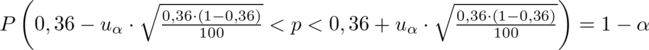
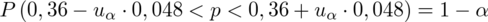
Jak widać, nie możemy uzupełnić współczynnika ufności
 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
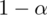 , a tym samym nieznana jest
, a tym samym nieznana jest
 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.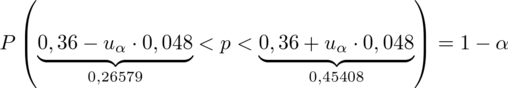
Nie znamy wartości
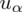 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,26579 czy 0,45408? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,26579 czy 0,45408? Jest to całkowicie obojętne, ponieważ w obu przypadkach
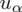 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
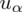 , więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,26579 czy 0,45408? Jest to całkowicie obojętne, ponieważ w obu przypadkach
, więc potraktujmy ją jak niewiadomą i rozwiążemy równanie aby ją wyznaczyć. Którą końcówkę przedziału wybrać tzn. 0,26579 czy 0,45408? Jest to całkowicie obojętne, ponieważ w obu przypadkach
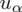 jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład:
jest tą samą wartością. Poza tym szukamy jednej niewiadomej, a do wyznaczenia jednej niewiadomej wystarczy jedno równanie. A więc na przykład: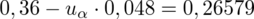
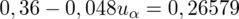
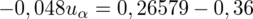
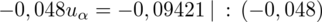
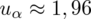
Jeśli komuś z Was jest wygodniej rozwiązywać równania z literką x, to może nią spokojnie na początku zastąpić symbol
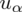 .
.
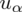 .
.
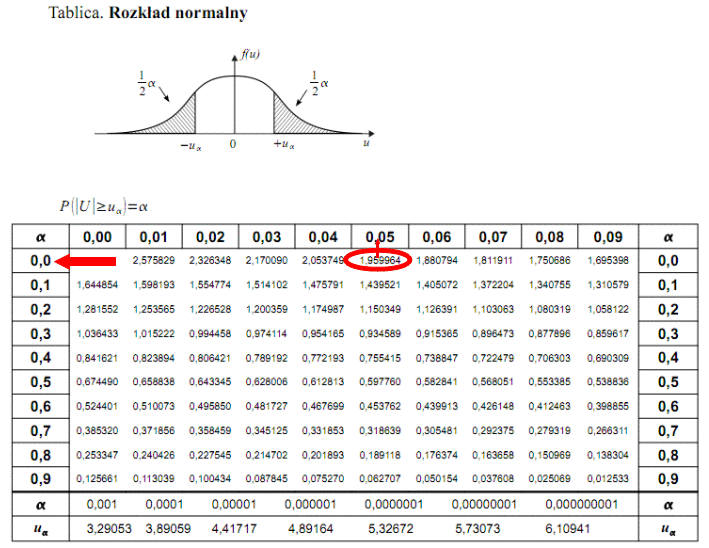
Dopiero teraz wracamy do odczytywania z tablic, jest to tzw. „zadanie od tyłu”, więc i z tablic czytamy od tyłu, a więc szukamy wartości najbliższej
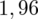 , ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
, ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
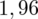 we wnętrzu tablicy stanowi
we wnętrzu tablicy stanowi
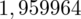 . Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
. Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
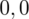 i
i
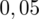 , czyli
, czyli
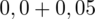 . Pamiętajmy, że jest to
. Pamiętajmy, że jest to
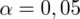 .
.
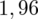 , ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
, ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle. Najbliższą wartością
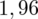 we wnętrzu tablicy stanowi
we wnętrzu tablicy stanowi
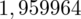 . Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
. Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
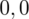 i
i
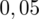 , czyli
, czyli
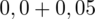 . Pamiętajmy, że jest to
. Pamiętajmy, że jest to
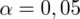 .
.
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy współczynnik ufności
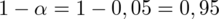 , a więc prawidłowa jest odpowiedź B.
, a więc prawidłowa jest odpowiedź B.
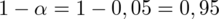 , a więc prawidłowa jest odpowiedź B.
, a więc prawidłowa jest odpowiedź B.
Interpretacja brzmi następująco (nie jest tu potrzebna): Z ufnością 0,95 odsetek studentów zamieszkujących na stale w Białymstoku mieści się w przedziale od 26,579% do 45,408%.