
W pobranej w sposób niezależny 900-osobowej grupie emerytów i rencistów zamieszkałych w Warszawie średnio 12 osób na 100 otrzymało w ostatnim miesiącu przed badaniem świadczenia w wysokości od 300 do 400 PLN. Zbudować przedział ufności dla odsetka ogółu emerytów i rencistów zamieszkałych w Warszawie, pobierających emerytury lub renty w wysokości od 300 do 400 PLN. Przyjąć współczynnik ufności równy 0,98.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdania:
Zbudować przedział ufności dla odsetka ogółu emerytów i rencistów zamieszkałych w Warszawie, pobierających emerytury lub renty w wysokości od 300 do 400 PLN. Przyjąć współczynnik ufności równy 0,98.
Występują tu zwroty: zbudować przedział ufności i współczynnik ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
W pobranej w sposób niezależny 900-osobowej grupie emerytów i rencistów zamieszkałych w Warszawie średnio 12 osób na 100 otrzymało w ostatnim miesiącu przed badaniem świadczenia w wysokości od 300 do 400 PLN.
Od razu zaczyna się opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości osób spośród wszystkich emerytów i rencistów zamieszkałych w Warszawie. Oznaczamy więc liczebność próby
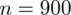 . Dowiadujemy się również, że 12 osób na 100 otrzymuje świadczenia w wysokości od 300 do 400 PLN - jest to wskaźnik struktury w próbie
. Dowiadujemy się również, że 12 osób na 100 otrzymuje świadczenia w wysokości od 300 do 400 PLN - jest to wskaźnik struktury w próbie
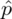 , tylko podany w nieco innej formie
, tylko podany w nieco innej formie
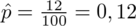 . Na upartego można wyliczyć ile osób spośród próby otrzymuje świadczenia od 300 do 400 PLN. Wystarczy zastosować zwykłą proporcję:
. Na upartego można wyliczyć ile osób spośród próby otrzymuje świadczenia od 300 do 400 PLN. Wystarczy zastosować zwykłą proporcję:
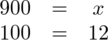 . Po przekształceniu otrzymujemy
. Po przekształceniu otrzymujemy
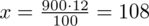 i jest to ilość obserwacji wyróżnionych spośród próby, a więc
i jest to ilość obserwacji wyróżnionych spośród próby, a więc
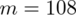 . Dalsze obliczenia będziemy jednak wykonywać z użyciem wskaźnika struktury z próby
. Dalsze obliczenia będziemy jednak wykonywać z użyciem wskaźnika struktury z próby
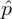 , ponieważ będą krótsze.
, ponieważ będą krótsze.
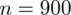 . Dowiadujemy się również, że 12 osób na 100 otrzymuje świadczenia w wysokości od 300 do 400 PLN - jest to wskaźnik struktury w próbie
. Dowiadujemy się również, że 12 osób na 100 otrzymuje świadczenia w wysokości od 300 do 400 PLN - jest to wskaźnik struktury w próbie
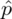 , tylko podany w nieco innej formie
, tylko podany w nieco innej formie
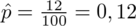 . Na upartego można wyliczyć ile osób spośród próby otrzymuje świadczenia od 300 do 400 PLN. Wystarczy zastosować zwykłą proporcję:
. Na upartego można wyliczyć ile osób spośród próby otrzymuje świadczenia od 300 do 400 PLN. Wystarczy zastosować zwykłą proporcję:
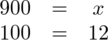 . Po przekształceniu otrzymujemy
. Po przekształceniu otrzymujemy
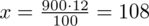 i jest to ilość obserwacji wyróżnionych spośród próby, a więc
i jest to ilość obserwacji wyróżnionych spośród próby, a więc
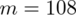 . Dalsze obliczenia będziemy jednak wykonywać z użyciem wskaźnika struktury z próby
. Dalsze obliczenia będziemy jednak wykonywać z użyciem wskaźnika struktury z próby
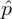 , ponieważ będą krótsze.
, ponieważ będą krótsze.
Zbudować przedział ufności dla odsetka ogółu emerytów i rencistów zamieszkałych w Warszawie, pobierających emerytury lub renty w wysokości od 300 do 400 PLN.
W tym zdaniu nie ma ważnych informacji z punktu widzenia danych potrzebnych do obliczeń. Podana wysokość świadczeń nie jest istotna.
Przyjąć współczynnik ufności równy 0,98.
Podano również współczynnik ufności
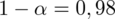 , od razu wyznaczamy
, od razu wyznaczamy
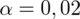 .
.
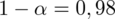 , od razu wyznaczamy
, od razu wyznaczamy
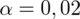 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
emeryci i renciści zamieszkali w Warszawie |
PRÓBA
900 wybranych emerytów i rencistów |
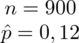
|
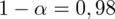 - współczynnik ufności,
- współczynnik ufności,
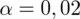
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w przedostatnim zdaniu wyłapujemy słowo:
Zbudować przedział ufności dla odsetka ogółu emerytów i rencistów zamieszkałych w Warszawie, pobierających emerytury lub renty w wysokości od 300 do 400 PLN.
Słowo odsetek oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy do wyboru dwie formuły. W danych wypisano
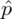 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, (w analizie zostało to zrobione). Jednak użycie drugiego wzoru odrobinę ułatwi obliczenia.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, (w analizie zostało to zrobione). Jednak użycie drugiego wzoru odrobinę ułatwi obliczenia.
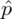 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, (w analizie zostało to zrobione). Jednak użycie drugiego wzoru odrobinę ułatwi obliczenia.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, (w analizie zostało to zrobione). Jednak użycie drugiego wzoru odrobinę ułatwi obliczenia.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
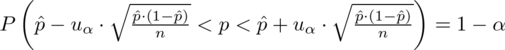 konkretnymi danymi.
konkretnymi danymi.
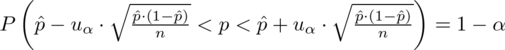 konkretnymi danymi.
konkretnymi danymi.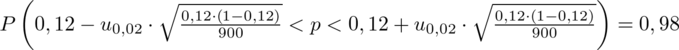
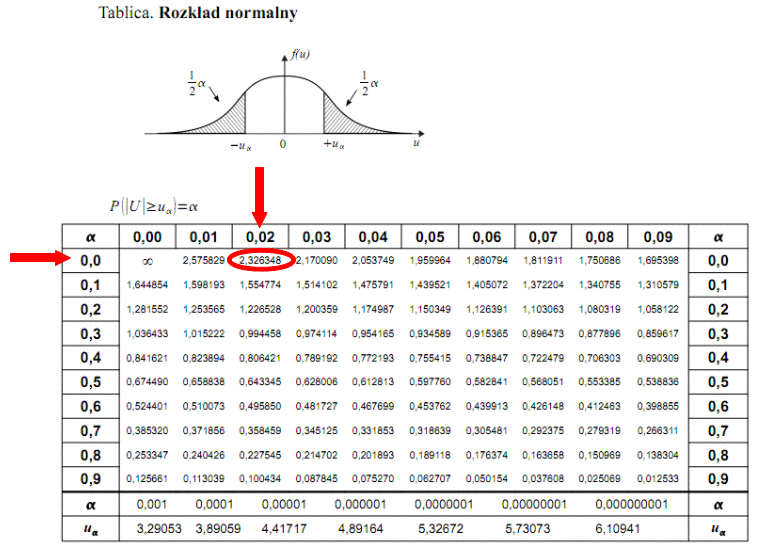
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
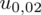 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
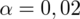 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
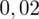 sumujemy
sumujemy
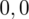 i
i
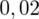 czyli
czyli
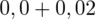 .
.
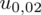 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
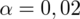 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
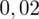 sumujemy
sumujemy
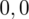 i
i
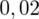 czyli
czyli
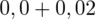 .
.
Wracamy do obliczeń i podstawiamy
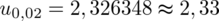 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
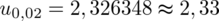 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):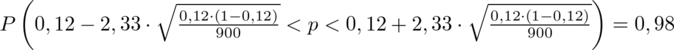
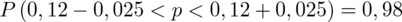
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
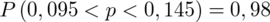
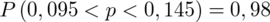
Interpretacja brzmi następująco: Z ufnością 0,98 odsetek ogółu emerytów i rencistów zamieszkałych w Warszawie, pobierających emerytury lub renty w wysokości od 300 do 400 PLN mieści się w przedziale od 0,095 do 0,145.
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4