
Z prawdopodobieństwem 0,95 oszacować, jaka część młodzieży szkół średnich pali papierosy, jeżeli w próbie liczącej 1000 uczniów wybranych w losowaniu niezależnym, 360 uczniów paliło papierosy.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na część zdania:
Z prawdopodobieństwem 0,95 oszacować, jaka część młodzieży...
Co prawda nie użyto bezpośrednio zwrotu przedział ufności, ale musimy oszacować część młodzieży palącą papierosy, więc wypadałoby podać przedział ufności, bo tzw. estymacja punktowa (tzn. konkretna liczba, a nie przedział) daje wynik o prawdopodobieństwie praktycznie równym zero. Dodatkowo występuje tu wyrażenie: prawdopodobieństwo = współczynnik ufności i w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zadanie.
Z prawdopodobieństwem 0,95 oszacować, jaka część młodzieży szkół średnich pali papierosy, jeżeli w próbie liczącej 1000 uczniów wybranych w losowaniu niezależnym, 360 uczniów paliło papierosy.
Na wstępie podano prawdopodobieństwo, czyli współczynnik ufności
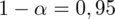 , od razu wyznaczamy
, od razu wyznaczamy
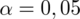 . Później zaczyna się opis próby, ponieważ pojawia się informacja na temat badania konkretnej ilości uczniów spośród wszystkich uczniów szkół średnich. Oznaczamy więc liczebność próby
. Później zaczyna się opis próby, ponieważ pojawia się informacja na temat badania konkretnej ilości uczniów spośród wszystkich uczniów szkół średnich. Oznaczamy więc liczebność próby
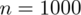 . Ponadto uzyskujemy informację, że 360 uczniów spośród 1000 pali papierosy - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Ponadto uzyskujemy informację, że 360 uczniów spośród 1000 pali papierosy - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
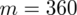 .
.
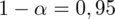 , od razu wyznaczamy
, od razu wyznaczamy
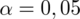 . Później zaczyna się opis próby, ponieważ pojawia się informacja na temat badania konkretnej ilości uczniów spośród wszystkich uczniów szkół średnich. Oznaczamy więc liczebność próby
. Później zaczyna się opis próby, ponieważ pojawia się informacja na temat badania konkretnej ilości uczniów spośród wszystkich uczniów szkół średnich. Oznaczamy więc liczebność próby
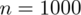 . Ponadto uzyskujemy informację, że 360 uczniów spośród 1000 pali papierosy - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
. Ponadto uzyskujemy informację, że 360 uczniów spośród 1000 pali papierosy - jest to ilość wyróżnionych obserwacji spośród próby. Opisujemy ją symbolem
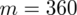 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
wszyscy uczniowie szkół średnich |
PRÓBA
1000 wybranych uczniów |
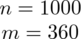
|
 - współczynnik ufności,
- współczynnik ufności,
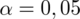
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności wyłapując w zadaniu słowo:
Z prawdopodobieństwem 0,95 oszacować, jaka część młodzieży szkół średnich pali papierosy, jeżeli w próbie liczącej 1000 uczniów wybranych w losowaniu niezależnym, 360 uczniów paliło papierosy.
Słowo część nie jest mocno charakterystyczne, ale będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Na wskaźnik struktury wskazuje również wypisana w danych ilość wyróżnionych obserwacji spośród próby oznaczana jako m. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy dwie formuły. W danych wypisano m w związku z tym wybieramy pierwszy wzór. Oczywiście można użyć drugiego wzoru, bo są one równoważne, ale na początku należy wyliczyć wskaźnik struktury z próby
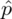 .
.
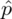 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
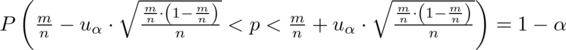 konkretnymi danymi.
konkretnymi danymi.
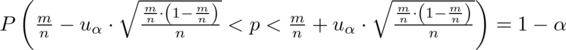 konkretnymi danymi.
konkretnymi danymi.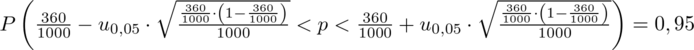
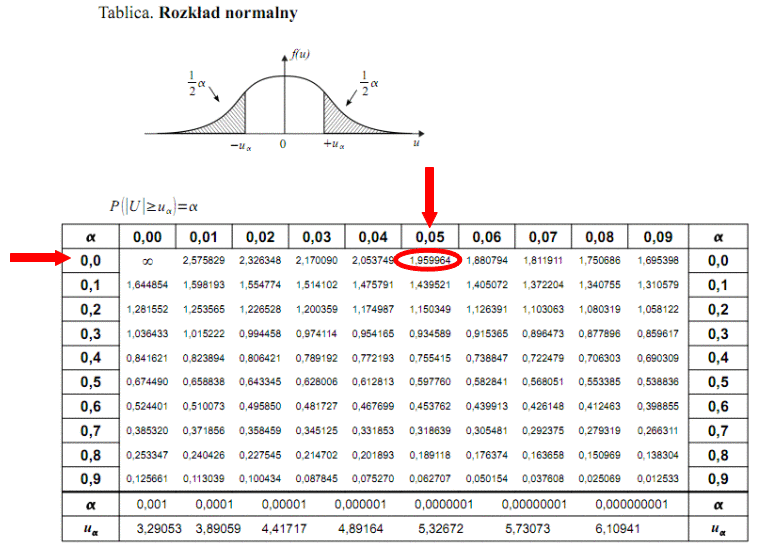
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
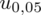 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
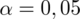 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
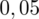 sumujemy
sumujemy
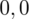 i
i
 czyli
czyli
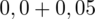 .
.
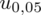 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
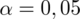 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
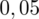 sumujemy
sumujemy
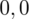 i
i
 czyli
czyli
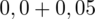 .
.
Wracamy do obliczeń i podstawiamy
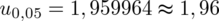 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
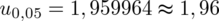 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)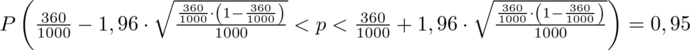
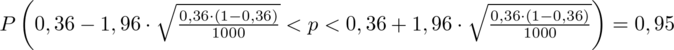
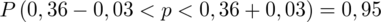
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
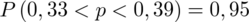
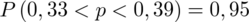
Interpretacja brzmi następująco: Z ufnością 0,95 część młodzieży szkół średnich palących papierosy z populacji wszystkich uczniów mieści się w przedziale od 0,33 do 0,39.
Statystyka: podstawy teoretyczne, przykłady, zadania / Mieczysław Sobczyk. - Wyd.1 - Lublin : Wydaw.Uniw.M.Curie-Skłodowskiej, 2000 - 425 s. ; 25 cm. - ISBN 83-227-1608-7