
W firmie produkującej chemikalia z populacji 800 robotników wylosowano niezależną próbę o liczebności 260 osób w celu przeprowadzenia ankiety dotyczącej m.in. warunków pracy. Okazało się, że 70% wylosowanych robotników oceniło warunki pracy jako niezadowalające. Przyjmując współczynnik ufności 0,95, zbudować przedział ufności dla frakcji robotników niezadowolonych z warunków pracy.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
Przyjmując współczynnik ufności 0,95, zbudować przedział ufności dla frakcji robotników niezadowolonych z warunków pracy.
Występują tu zwroty: zbudować przedział ufności i współczynnik ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
W firmie produkującej chemikalia z populacji 800 robotników wylosowano niezależną próbę o liczebności 260 osób w celu przeprowadzenia ankiety dotyczącej m.in. warunków pracy.
Dowiadujemy się, że populacja robotników liczy 800 osób, więc oznaczamy jej liczebność jako
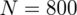 . Później mamy już opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości robotników. Oznaczamy więc liczebność próby
. Później mamy już opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości robotników. Oznaczamy więc liczebność próby
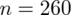 .
.
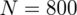 . Później mamy już opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości robotników. Oznaczamy więc liczebność próby
. Później mamy już opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości robotników. Oznaczamy więc liczebność próby
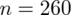 .
.
Okazało się, że 70% wylosowanych robotników oceniło warunki pracy jako niezadowalające.
Ponadto dowiadujemy się, że 70% robotników oceniło warunki pracy negatywnie. Jest to procent procent robotników, a więc wskaźnik struktury w próbie. Opisujemy go symbolem
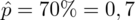 .
.
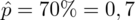 .
.
Przyjmując współczynnik ufności 0,95, zbudować przedział ufności dla frakcji robotników niezadowolonych z warunków pracy.
Podano również współczynnik ufności
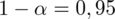 , od razu wyznaczamy
, od razu wyznaczamy
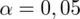 .
.
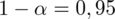 , od razu wyznaczamy
, od razu wyznaczamy
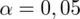 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
POPULACJA
800 robotników |
PRÓBA
260 wybranych robotników |
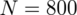
|
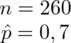
|
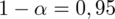 - współczynnik ufności,
- współczynnik ufności,
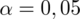
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
Przyjmując współczynnik ufności 0,95, zbudować przedział ufności dla frakcji robotników niezadowolonych z warunków pracy.
Słowo frakcja oznacza, że będziemy budować przedział ufności dla wskaźnika struktury p z populacji. Spójrzmy w kartę wzorów. Dla wskaźnika struktury mamy do wyboru dwie formuły. W danych wypisano
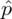 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
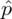 w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
w związku z tym użyjemy drugiego wzoru. Oczywiście można wybrać pierwszy wzór, bo są one równoważne, ale na początku należałoby wyliczyć ilość wyróżnionych obserwacji spośród próby czyli m, a o to nas w zadaniu nie pytają, więc nie dokładajmy sobie dodatkowych niepotrzebnych obliczeń.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych z tabeli i uzupełniamy wzór
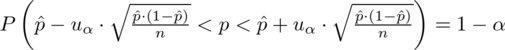 konkretnymi danymi.
konkretnymi danymi.
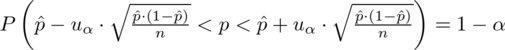 konkretnymi danymi.
konkretnymi danymi.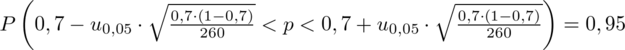
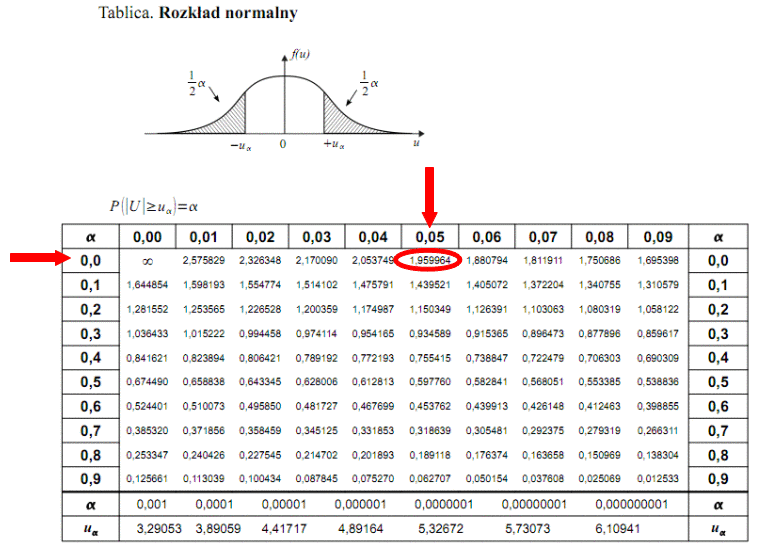
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego (link). Zapis
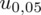 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
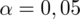 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
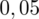 sumujemy
sumujemy
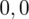 i
i
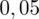 czyli
czyli
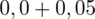 .
.
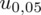 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla
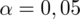 . Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
. Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku
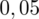 sumujemy
sumujemy
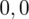 i
i
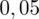 czyli
czyli
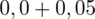 .
.
Wracamy do obliczeń i podstawiamy
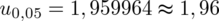 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
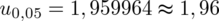 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)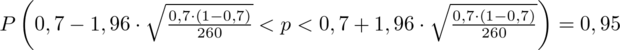
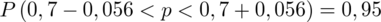
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy:
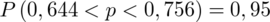
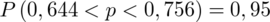
Interpretacja brzmi następująco: Z ufnością 0,95 frakcja robotników niezadowolonych z warunków pracy mieści się w przedziale od 0,644 do 0,756. Po zamianie na procent (czyli mnożenie przez 100%) przedział kształtuje się od 64,4% do 75,6%.
Statystyka: podstawy teoretyczne, przykłady, zadania / Mieczysław Sobczyk. - Wyd.1 - Lublin : Wydaw.Uniw.M.Curie-Skłodowskiej, 2000 - 425 s. ; 25 cm. - ISBN 83-227-1608-7