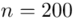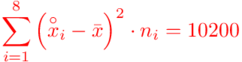Zadanie 43
Spośród kandydatów na studia ekonomiczne wybrano w losowaniu niezależnym 200 osób i zbadano je testem logicznego myślenia. Otrzymano następujące wyniki (w punktach):
|
Wyniki testu |
5 - 9 |
10 - 14 |
15 - 19 |
20 - 24 |
25 - 29 |
30 - 34 |
35 - 39 |
40 - 44 |
|
Liczba osób |
2 |
16 |
25 |
50 |
50 |
40 |
15 |
2 |
Oszacować metodą przedziałową średni wynik testu logicznego myślenia wśród kandydatów. Przyjąć współczynnik ufności 0,95 oraz 0,99. Które oszacowanie jest bardziej precyzyjne?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdania:
„Oszacować metodą przedziałową średni wynik testu logicznego myślenia wśród kandydatów. Przyjąć współczynnik ufności 0,95 oraz 0,99.”
Odnajdujemy w nich zwroty: oszacować metodą przedziałową i współczynnik ufności. Teraz mamy pewność, że zadanie dotyczy estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Spośród kandydatów na studia ekonomiczne wybrano w losowaniu niezależnym 200 osób i zbadano je testem logicznego myślenia.”
W tym momencie wiemy, że wylosowano próbę, a jej liczebność to 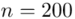 osób i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
osób i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
„Otrzymano następujące wyniki (w punktach):”
|
Wyniki testu |
5 - 9 |
10 - 14 |
15 - 19 |
20 - 24 |
25 - 29 |
30 - 34 |
35 - 39 |
40 - 44 |
|
Liczba osób |
2 |
16 |
25 |
50 |
50 |
40 |
15 |
2 |
Podano również wyniki z próby w tabeli. Jeżeli dysponujemy danymi dotyczącymi próby ujętymi w tabeli zawsze możemy policzyć średnią 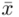 , wariancję
, wariancję 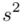 i odchylenie standardowe
i odchylenie standardowe 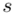 (lub
(lub 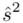 ,
, 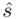 ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
„Oszacować metodą przedziałową średni wynik testu logicznego myślenia wśród kandydatów.”
Z punktu widzenia analizy danych nie mamy w tym zdaniu istotnych informacji.
„Przyjąć współczynnik ufności 0,95 oraz 0,99. Które oszacowanie jest bardziej precyzyjne?”
Podano też współczynniki ufności 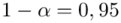 i
i 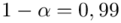 , od razu wyznaczamy odpowiednio
, od razu wyznaczamy odpowiednio 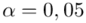 i
i 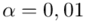 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA kandydaci na studia ekonomiczne |
PRÓBA 200 wybranych osób |
|
|
dane tabelaryczne - (można obliczyć średnią |
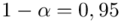 - współczynnik ufności,
- współczynnik ufności, 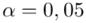
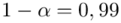 - współczynnik ufności,
- współczynnik ufności, 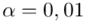
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w końcówce zadania wyłapujemy słowo:
„Oszacować metodą przedziałową średni wynik testu logicznego myślenia wśród kandydatów. ”
Słowo średni oznacza, że będziemy budować przedział ufności dla wartości średniej 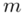 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 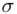 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 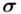 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 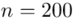 jest większa od 30 (
jest większa od 30 ( 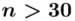 ), zatem wybieramy model III.
), zatem wybieramy model III.

Ten sam wzór będzie użyty dla obydwu przyjętych współczynników ufności. Oprócz podania przedziałów ufności należy określić stopień precyzji oszacowania obu wyników. Najbardziej miarodajnym miernikiem jest względna precyzja szacunku 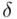 określona wzorem
określona wzorem 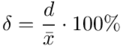 , gdzie
, gdzie 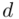 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej 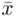
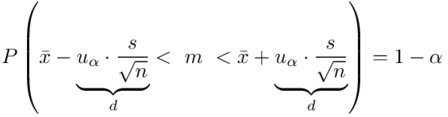
czyli 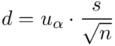 . Powtarzam jeszcze raz, że formuła na obliczenie
. Powtarzam jeszcze raz, że formuła na obliczenie 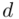 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej 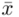 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 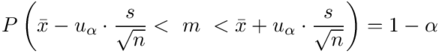 konkretnymi liczbami. Jak widać potrzebujemy średniej z próby
konkretnymi liczbami. Jak widać potrzebujemy średniej z próby 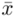 i odchylenia standardowego
i odchylenia standardowego 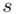 . W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
. W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
Dysponujemy danymi tabelarycznymi, gdzie warianty cechy (wyniki testu) są w formie przedziałów tzn. od jednej wartości do drugiej wartości. Taki szereg określa się szeregiem rozdzielczym przedziałowym. Przeredagujmy zatem tabelę z zadania właśnie na tą postać szeregu.
|
(wyniki testu) |
(liczba osób) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W przypadku szeregu rozdzielczego przedziałowego nie ma możliwości pomyłki do tego co jest wariantem cechy, a co liczebnością 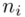 , ponieważ nie zdarza się, aby
, ponieważ nie zdarza się, aby 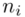 było zapisane w formie przedziałów. Symbol
było zapisane w formie przedziałów. Symbol 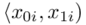 to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. Tabela z zadania niestety nie spełnia tego wymogu np.
to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. Tabela z zadania niestety nie spełnia tego wymogu np.  ,
,  (przedział kończy się 9, następny zaczyna się od 10), itd. w związku z tym musimy nieco przebudować przedziały aby zachować ciągłość. Liczebności poszczególnych przedziałów nie ulegają zmianie. Co prawda spotkałam się z obliczeniami bez zachowania ciągłości, niemniej jednak były to wyjątki. Jeśli nie jesteśmy pewni jak mamy postępować w takim przypadku, po prostu spytajmy prowadzącego zajęcia. Z reguły zmianie ulegają końcówki przedziałów, a początki pozostają bez zmian. Zaczynamy od 5 i zamiast 9 przedział zakończymy na 10, ponieważ kolejny zaczyna się właśnie od 10 itd. Sama dziesiątka i tak nie wchodzi do pierwszego przedziału, ponieważ jest on prawostronnie otwarty. Tabela z przebudowanymi przedziałami wygląda następująco:
(przedział kończy się 9, następny zaczyna się od 10), itd. w związku z tym musimy nieco przebudować przedziały aby zachować ciągłość. Liczebności poszczególnych przedziałów nie ulegają zmianie. Co prawda spotkałam się z obliczeniami bez zachowania ciągłości, niemniej jednak były to wyjątki. Jeśli nie jesteśmy pewni jak mamy postępować w takim przypadku, po prostu spytajmy prowadzącego zajęcia. Z reguły zmianie ulegają końcówki przedziałów, a początki pozostają bez zmian. Zaczynamy od 5 i zamiast 9 przedział zakończymy na 10, ponieważ kolejny zaczyna się właśnie od 10 itd. Sama dziesiątka i tak nie wchodzi do pierwszego przedziału, ponieważ jest on prawostronnie otwarty. Tabela z przebudowanymi przedziałami wygląda następująco:
|
(wyniki testu) |
(liczba osób) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Przechodzimy do liczenia brakującej średniej i odchylenia standardowego.
W szeregu przedziałowym średnią liczymy ze wzoru 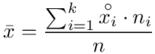 .
.
Na początku wyjaśnijmy symbol 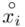 . Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły
. Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły 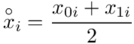 . Upraszczając należy zsumować początek
. Upraszczając należy zsumować początek 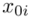 i koniec
i koniec 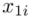 każdego przedziału i wynik podzielić na dwa.
każdego przedziału i wynik podzielić na dwa.
Wracamy do wzoru na średnią. Znak 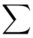 oznacza sumę. Pod tym symbolem znajduje się zapis
oznacza sumę. Pod tym symbolem znajduje się zapis 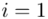 , a nad nim
, a nad nim 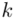 ,
, 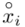 to środki kolejnych przedziałów, a
to środki kolejnych przedziałów, a 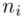 liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny
liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny 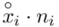 , gdzie
, gdzie 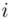 będzie rosło od
będzie rosło od 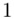 aż do wartości
aż do wartości 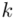 , a więc
, a więc 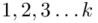 , a więc ogólnie:
, a więc ogólnie:
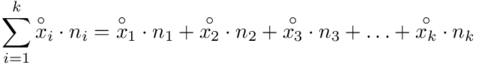
W naszym przypadku 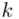 znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
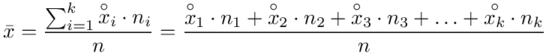
Czym jest 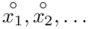 ,
, 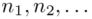 oraz
oraz 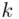 ? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
|
Numer klasy |
(wiek pracowników) |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uzupełniając 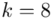 otrzymujemy wzór:
otrzymujemy wzór:
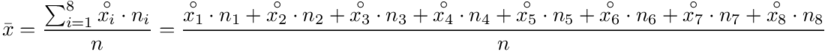 i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość
i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość 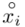 mnożymy przez odpowiadającą jej wartość
mnożymy przez odpowiadającą jej wartość 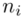 , a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem
, a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem 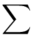 i kolumny
i kolumny 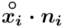 daje kompletny licznik wzoru na średnią.
daje kompletny licznik wzoru na średnią.
|
Numer klasy |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
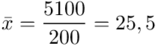
Zostało nam jeszcze odchylenie standardowe 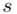 . Na początek i tak musimy obliczyć wariancję
. Na początek i tak musimy obliczyć wariancję 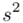 , bo
, bo 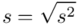 . Wzór na wariancję z danych szeregu przedziałowego wygląda następująco:
. Wzór na wariancję z danych szeregu przedziałowego wygląda następująco: 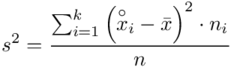 . Jest też alternatywa
. Jest też alternatywa 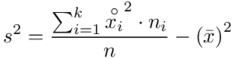 , ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
, ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
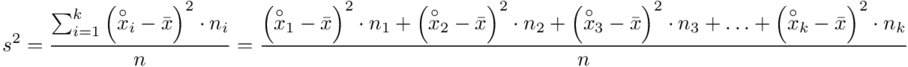
i dla ilości klas z zadania 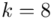 :
:
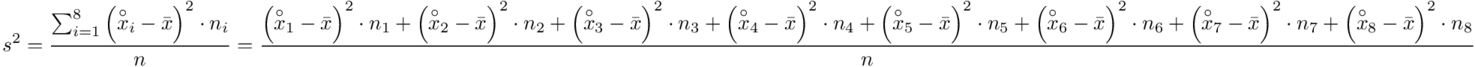
Tu też można podstawiać dane z tabeli, ale ponownie proponuję trzymać się obliczeń tabelarycznych. Można kontynuować poprzednią tabelę dopisując kolejne kolumny. Znowu krok po kroku będziemy tworzyć licznik ze wzoru. Dopisana pierwsza kolumna - od każdego środka przedziału 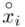 odejmujemy wcześniej wyliczoną średnią
odejmujemy wcześniej wyliczoną średnią 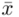 , druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości
, druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości 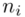 i dopiero ona jest sumowana (przecięcie wiersza z symbolem
i dopiero ona jest sumowana (przecięcie wiersza z symbolem 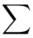 i
i 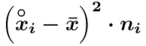 daje kompletny licznik wzoru na wariancję ).
daje kompletny licznik wzoru na wariancję ).
|
Numer klasy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
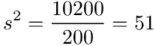
Odchylenie standardowe 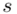 to pierwiastek z wariancji
to pierwiastek z wariancji 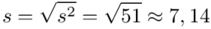 .
.
Wracamy do istoty zadania i wreszcie uzupełniamy wzór 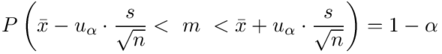 . Na początku przyjmiemy współczynnik ufności
. Na początku przyjmiemy współczynnik ufności 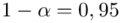 (
( 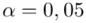 ), a następnie
), a następnie 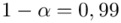 (
( 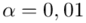 ).
).
Dla 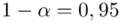 otrzymujemy:
otrzymujemy:
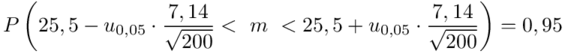
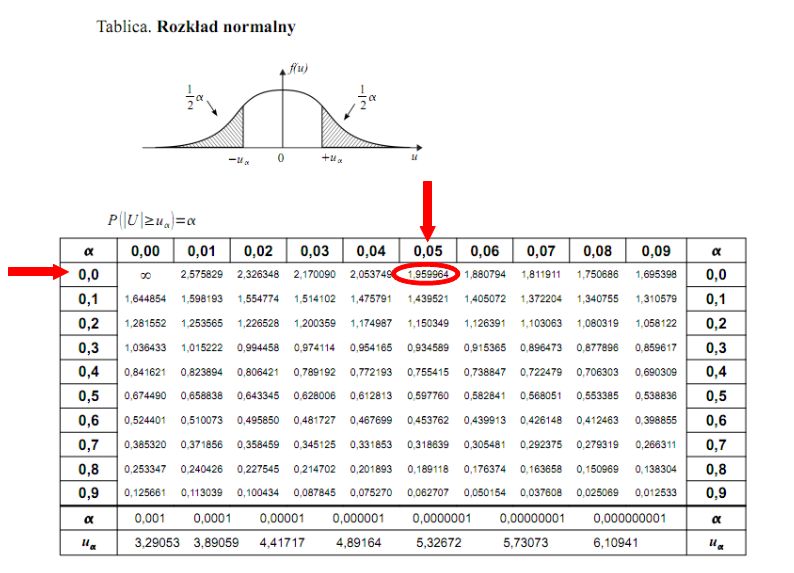
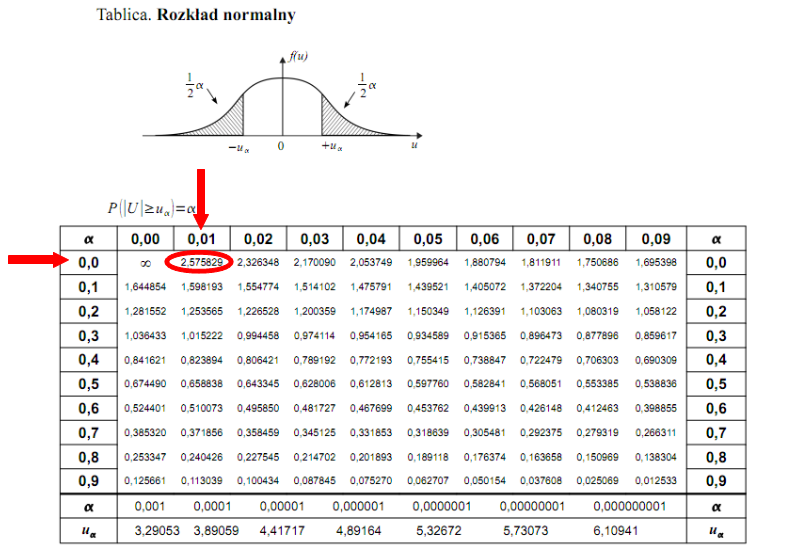
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego. Zapis 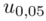 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla 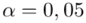 .
.
Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku 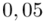 sumujemy
sumujemy 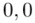 i
i 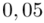 czyli
czyli 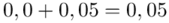 .
.
Wracamy do obliczeń i podstawiamy 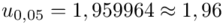 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
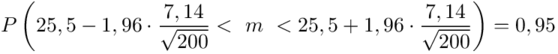
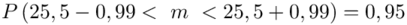
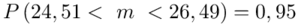
Z kolei dla 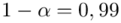 otrzymujemy:
otrzymujemy:
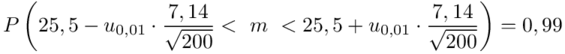
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego. Zapis 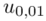 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla 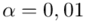 .
.
Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku 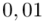 sumujemy
sumujemy 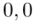 i
i 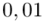 czyli
czyli 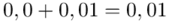 .
.
Wracamy do obliczeń i podstawiamy 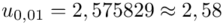 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
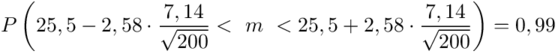
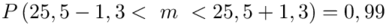
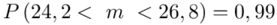
Analogicznie określimy względną precyzję szacunku 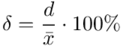 , gdzie
, gdzie 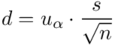 .
.
Względna precyzja szacunku dla 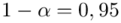 :
:
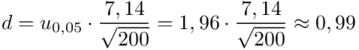 , tak więc
, tak więc 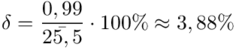 .
.
Względna precyzja szacunku dla 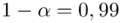 :
:
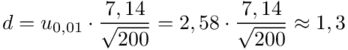 , tak więc
, tak więc 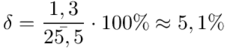 .
.
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy dla 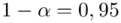 :
: 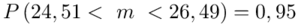
Interpretacja brzmi następująco:
Z ufnością 0,95 nieznany średni wynik testu logicznego myślenia dla ogółu kandydatów mieści się się w przedziale od 24,51 punktów do 26,49 punktów.
Ostatecznie otrzymujemy dla 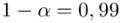 :
: 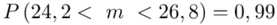
Interpretacja brzmi następująco:
Z ufnością 0,99 nieznany średni wynik testu logicznego myślenia dla ogółu kandydatów mieści się się w przedziale od 24,2 punktów do 26,8 punktów.
Po zmianie współczynnika ufności z 0,95 do 0,99 względna precyzja oszacowania zmalała z poziomu 3,88% do 5,1%. Coś tu jednak się nie zgadza, prawda? Przecież po zwiększeniu współczynnika ufności otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu? Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość 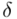 poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku
poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku 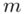 ) jest uprawnione i całkowicie bezpieczne, jeżeli
) jest uprawnione i całkowicie bezpieczne, jeżeli 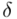 mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli
mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli 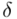 przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku
przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku 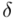 może być spowodowane zbyt wysokim współczynnikiem ufności, zbyt małą liczebnością próby oraz wysokim zróżnicowaniem wyników w próbie (np. duży rozstrzał danych). Tak więc oszacowanie przy współczynniku ufności 0,95 jest bardziej precyzyjne.
może być spowodowane zbyt wysokim współczynnikiem ufności, zbyt małą liczebnością próby oraz wysokim zróżnicowaniem wyników w próbie (np. duży rozstrzał danych). Tak więc oszacowanie przy współczynniku ufności 0,95 jest bardziej precyzyjne.
Statystyka: podstawy teoretyczne, przykłady, zadania / Mieczysław Sobczyk. - Wyd.1 - Lublin : Wydaw.Uniw.M.Curie-Skłodowskiej, 2000 - 425 s. ; 25 cm. - ISBN 83-227-1608-7
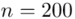
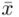 , wariancję
, wariancję 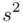 , odchylenie standardowe
, odchylenie standardowe 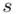 )
)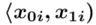 - warianty obserwacji
- warianty obserwacji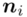 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych
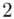

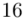

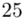

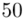

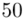

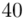

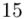

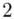
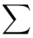 (suma)
(suma)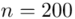
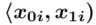 - warianty obserwacji
- warianty obserwacji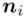 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych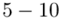
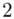

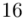

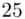

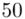

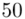

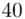

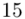

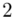
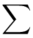 (suma)
(suma)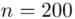
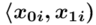 - przedziały klasowe
- przedziały klasowe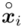 -
-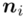 -liczebności poszczególnych przedziałów klasowych
-liczebności poszczególnych przedziałów klasowych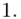
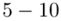
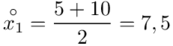
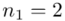
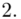

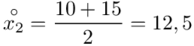
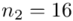
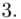

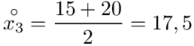
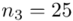
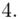

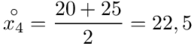
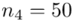
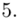

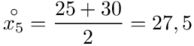
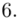

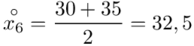
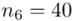
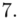

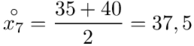
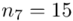
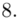

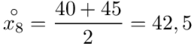
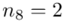
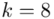
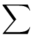 (suma)
(suma)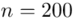
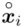 -
-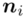 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych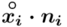
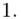
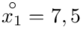
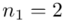
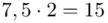
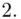
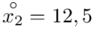
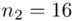
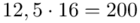
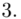
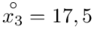
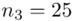
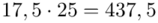
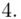
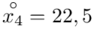
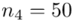
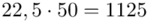
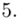
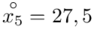
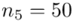
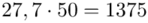
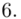
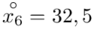
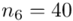
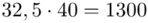
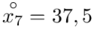
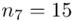
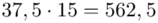
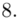
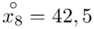
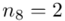
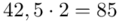
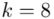
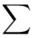 (suma)
(suma)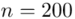
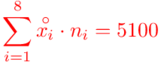
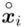 - środki przedziałów
- środki przedziałów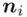 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych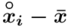
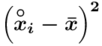
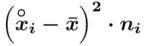
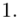
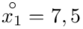
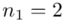
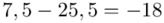
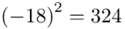
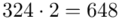
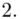
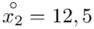
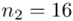
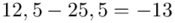
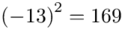
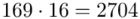
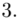
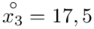
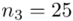
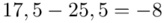
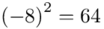
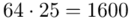
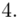
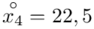
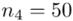
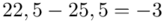
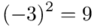
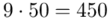
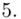
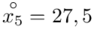
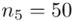
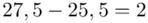
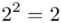
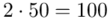
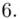
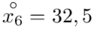
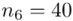
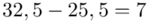
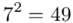
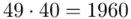
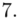
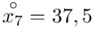
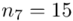
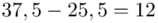
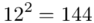
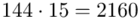
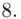
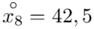
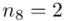
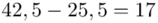
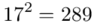
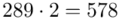
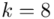
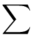 (suma)
(suma)