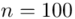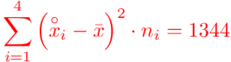Zadanie 41
Dla potrzeb oszacowania średniego trwania życia kineskopów pewnej klasy telewizorów wylosowano 100 kineskopów. Poniższe dane prezentują długość trwania życia wylosowanych kineskopów.
|
Długość trwania |
0 - 4 |
4 - 8 |
8 - 12 |
12 - 16 |
|
Ilość kineskopów |
10 |
40 |
30 |
20 |
Na poziomie 90% ufności oszacować przeciętne trwanie życia kineskopów badanej klasy.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
„Na poziomie 90% ufności oszacować przeciętne trwanie życia kineskopów badanej klasy.”
Co prawda nie użyto bezpośrednio zwrotu przedział ufności, ale musimy oszacować trwanie życia kineskopów, więc wypadałoby podać przedział ufności, bo tzw. estymacja punktowa (tzn. konkretna liczba, a nie przedział) daje wynik o prawdopodobieństwie praktycznie równym zero. Dodatkowo występuje tu wyrażenie: poziom ufności i w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Dla potrzeb oszacowania średniego trwania życia kineskopów pewnej klasy telewizorów wylosowano 100 kineskopów.”
W tym momencie wiemy, że wylosowano próbę, a jej liczebność to 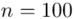 kineskopów i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
kineskopów i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
„Poniższe dane prezentują długość trwania życia wylosowanych kineskopów.”
|
Długość trwania |
0 - 4 |
4 - 8 |
8 - 12 |
12 - 16 |
|
Ilość kineskopów |
10 |
40 |
30 |
20 |
Podano również wyniki z próby w tabeli. Jeżeli dysponujemy danymi dotyczącymi próby ujętymi w tabeli zawsze możemy policzyć średnią 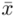 , wariancję
, wariancję 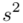 i odchylenie standardowe
i odchylenie standardowe 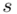 (lub
(lub 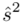 ,
, 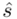 ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
„Na poziomie 90% ufności oszacować przeciętne trwanie życia kineskopów badanej klasy..”
Podano też współczynnik ufności  , od razu wyznaczamy
, od razu wyznaczamy 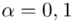 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA kineskopy pewnej klasy telewizorów |
PRÓBA 100 wybranych kineskopów |
|
|
dane tabelaryczne - (można obliczyć średnią |
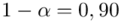 - współczynnik ufności,
- współczynnik ufności, 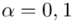
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
„Na poziomie 90% ufności oszacować przeciętne trwanie życia kineskopów badanej klasy. ”
Również w zdaniu pierwszym:
„Dla potrzeb oszacowania średniego trwania życia kineskopów pewnej klasy telewizorów wylosowano 100 kineskopów.”
Wyrażenie przeciętny/średniego oznacza, że będziemy budować przedział ufności dla wartości średniej 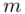 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 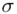 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 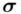 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 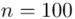 jest większa od 30 (
jest większa od 30 ( 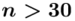 ), zatem wybieramy model III.
), zatem wybieramy model III.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 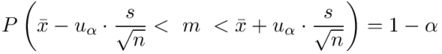 konkretnymi liczbami. Jak widać potrzebujemy średniej z próby
konkretnymi liczbami. Jak widać potrzebujemy średniej z próby 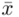 i odchylenia standardowego
i odchylenia standardowego 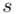 . W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
. W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
Dysponujemy danymi tabelarycznymi, gdzie warianty cechy (długość trwania życia) są w formie przedziałów tzn. od jednej wartości do drugiej wartości. Taki szereg określa się szeregiem rozdzielczym przedziałowym. Przeredagujmy zatem tabelę z zadania właśnie na tą postać szeregu.
|
(długość trwania życia) |
(liczba kineskopów) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W przypadku szeregu rozdzielczego przedziałowego nie ma możliwości pomyłki do tego co jest wariantem cechy, a co liczebnością 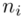 , ponieważ nie zdarza się, aby
, ponieważ nie zdarza się, aby 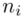 było zapisane w formie przedziałów. Symbol
było zapisane w formie przedziałów. Symbol 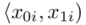 to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. W tabeli z zadania mamy właśnie przedstawioną sytuację
to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. W tabeli z zadania mamy właśnie przedstawioną sytuację  ,
,  (kończymy przedział na 4, następny również zaczynamy od 4), itd. w związku z tym nie musimy nic zmieniać, zachowana jest ciągłość.
(kończymy przedział na 4, następny również zaczynamy od 4), itd. w związku z tym nie musimy nic zmieniać, zachowana jest ciągłość.
W szeregu przedziałowym średnią liczymy ze wzoru 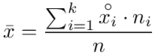 .
.
Na początku wyjaśnijmy symbol 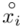 . Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły
. Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły 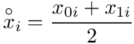 . Upraszczając należy zsumować początek
. Upraszczając należy zsumować początek 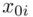 i koniec
i koniec 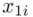 każdego przedziału i wynik podzielić na dwa.
każdego przedziału i wynik podzielić na dwa.
Wracamy do wzoru na średnią. Znak 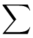 oznacza sumę. Pod tym symbolem znajduje się zapis
oznacza sumę. Pod tym symbolem znajduje się zapis 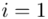 , a nad nim
, a nad nim 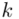 ,
, 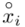 to środki kolejnych przedziałów, a
to środki kolejnych przedziałów, a 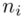 liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny
liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny 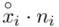 , gdzie
, gdzie 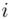 będzie rosło od
będzie rosło od 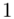 aż do wartości
aż do wartości 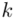 , a więc
, a więc 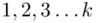 , a więc ogólnie:
, a więc ogólnie:
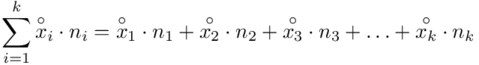
W naszym przypadku 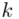 znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
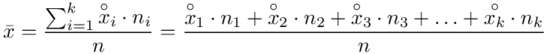
Czym jest 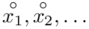 ,
, 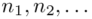 oraz
oraz 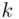 ? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
|
Numer klasy |
(wiek pracowników) |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uzupełniając 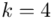 otrzymujemy wzór:
otrzymujemy wzór:
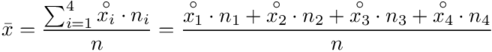 i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość
i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość 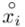 mnożymy przez odpowiadającą jej wartość
mnożymy przez odpowiadającą jej wartość 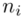 , a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem
, a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem 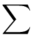 i kolumny
i kolumny 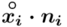 daje kompletny licznik wzoru na średnią.
daje kompletny licznik wzoru na średnią.
|
Numer klasy |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
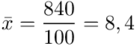
Zostało nam jeszcze odchylenie standardowe 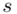 . Na początek i tak musimy obliczyć wariancję
. Na początek i tak musimy obliczyć wariancję 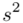 , bo
, bo 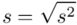 . Wzór na wariancję z danych szeregu przedziałowego wygląda następująco:
. Wzór na wariancję z danych szeregu przedziałowego wygląda następująco: 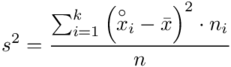 . Jest też alternatywa
. Jest też alternatywa 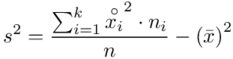 , ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
, ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
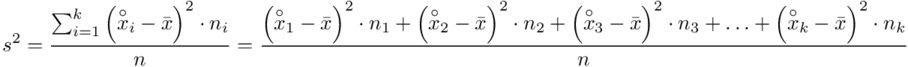
i dla ilości klas z zadania 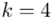 :
:
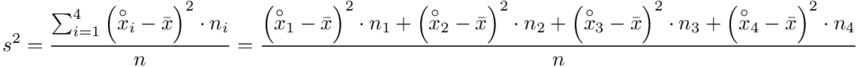
Tu też można podstawiać dane z tabeli, ale ponownie proponuję trzymać się obliczeń tabelarycznych. Można kontynuować poprzednią tabelę dopisując kolejne kolumny. Znowu krok po kroku będziemy tworzyć licznik ze wzoru. Dopisana pierwsza kolumna - od każdego środka przedziału 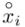 odejmujemy wcześniej wyliczoną średnią
odejmujemy wcześniej wyliczoną średnią 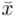 , druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości
, druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości 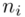 i dopiero ona jest sumowana (przecięcie wiersza z symbolem
i dopiero ona jest sumowana (przecięcie wiersza z symbolem 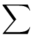 i
i 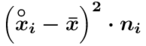 daje kompletny licznik wzoru na wariancję ).
daje kompletny licznik wzoru na wariancję ).
|
Numer klasy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
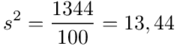
Odchylenie standardowe 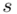 to pierwiastek z wariancji
to pierwiastek z wariancji 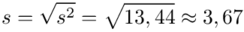 .
.
Wracamy do istoty zadania i wreszcie uzupełniamy wzór 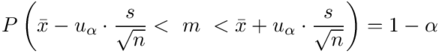 :
:
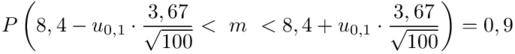
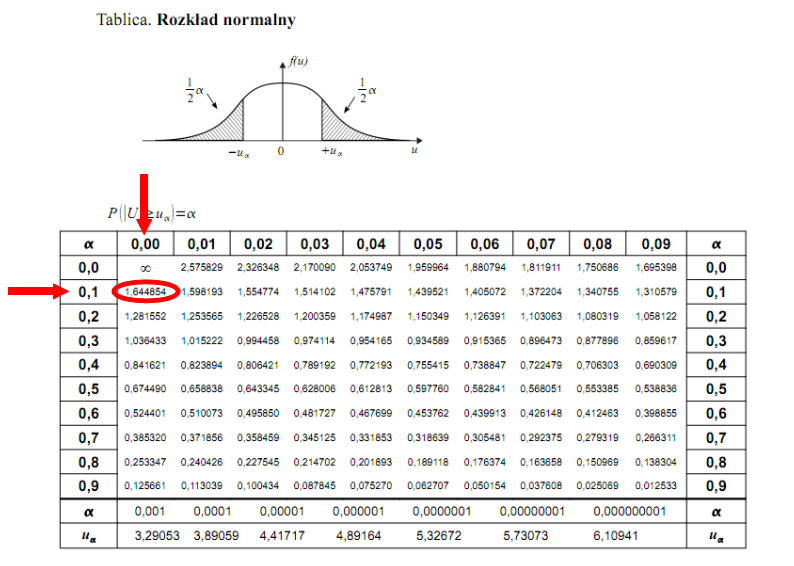
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego. Zapis 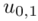 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla 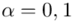 .
.
Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku 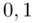 sumujemy
sumujemy 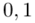 i
i 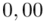 czyli
czyli 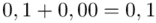 .
.
Wracamy do obliczeń i podstawiamy 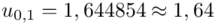 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
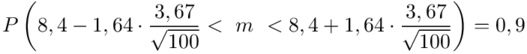
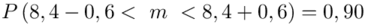
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy: 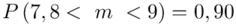
Interpretacja brzmi następująco:
Z ufnością 0,90 przeciętny czas trwania życia kineskopów badanej klasy mieści się w przedziale od 7,8 lat do 9 lat.
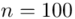
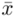 , wariancję
, wariancję 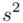 , odchylenie standardowe
, odchylenie standardowe 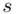 )
)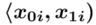 - warianty obserwacji
- warianty obserwacji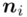 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych
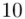

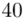
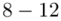
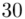

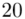
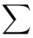 (suma)
(suma)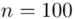
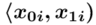 - przedziały klasowe
- przedziały klasowe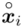 -
-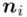 -liczebności poszczególnych przedziałów klasowych
-liczebności poszczególnych przedziałów klasowych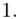

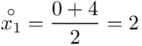
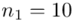
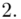

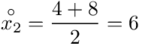
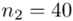
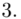
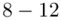
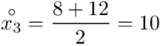
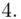

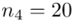
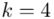
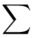 (suma)
(suma)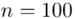
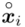 -
-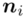 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych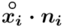
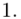
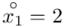
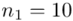
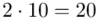
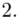
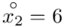
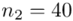
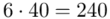
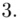
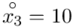
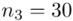
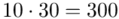
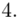
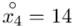
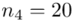
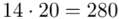
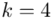
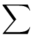 (suma)
(suma)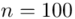
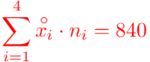
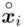 - środki przedziałów
- środki przedziałów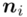 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych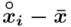
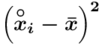
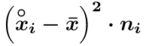
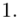
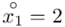
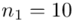
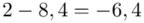
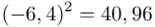
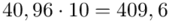
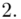
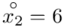
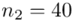
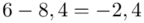
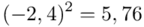
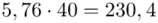
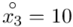
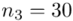
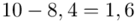
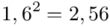
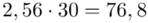
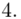
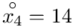
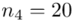
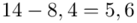
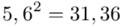
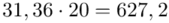
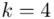
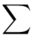 (suma)
(suma)