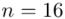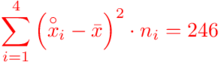Zadanie 40
W zakładzie Z dla 16 wybranych losowo pracowników otrzymano następujące informacje o zatrudnionych:
|
Wiek pracowników |
20-24 |
24-28 |
28-32 |
32-36 |
|
Liczba pracowników |
4 |
6 |
4 |
2 |
Zakładając, że rozkład wieku jest normalny, wyznaczyć przedział ufności dla przeciętnego wieku pracowników tego zakładu, jeśli poziom ufności wynosi 0,98.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu zadania zwracamy uwagę na ostatnie zdanie:
„Zakładając, że rozkład wieku jest normalny, wyznaczyć przedział ufności dla przeciętnego wieku pracowników tego zakładu, jeśli poziom ufności wynosi 0,98.”
Odnajdujemy w nim zwroty: wyznaczyć przedział ufności i poziom ufności. Teraz mamy pewność, że zadanie dotyczy estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„W zakładzie Z dla 16 wybranych losowo pracowników otrzymano następujące informacje o zatrudnionych:”
|
Wiek pracowników |
20-24 |
24-28 |
28-32 |
32-36 |
|
Liczba pracowników |
4 |
6 |
4 |
2 |
Losowo wybranych pracowników traktujemy jako próbę, a jej liczebność to 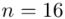 i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
Podano również wyniki z próby w tabeli. Jeżeli dysponujemy danymi dotyczącymi próby ujętymi w tabeli zawsze możemy policzyć średnią 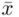 , wariancję
, wariancję 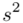 i odchylenie standardowe
i odchylenie standardowe 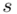 (lub
(lub 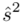 ,
, 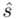 ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
„Zakładając, że rozkład wieku jest normalny, wyznaczyć przedział ufności dla przeciętnego wieku pracowników tego zakładu, jeśli poziom ufności wynosi 0,98.”
W zadaniu występuje założenie normalności rozkładu wieku i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Nie mamy informacji na temat tego rozkładu, zatem możemy tylko zapisać 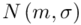 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 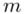 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 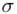 .
.
Podano też współczynnik ufności 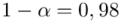 . Od razu wyznaczamy
. Od razu wyznaczamy 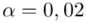 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA pracownicy zakładu Z |
PRÓBA 16 wybranych pracowników |
|
|
dane tabelaryczne - (można obliczyć średnią |
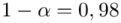 - współczynnik ufności,
- współczynnik ufności, 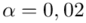
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
„Zakładając, że rozkład wieku jest normalny, wyznaczyć przedział ufności dla przeciętnego wieku pracowników tego zakładu, jeśli poziom ufności wynosi 0,98.” ”
Słowo przeciętnego oznacza, że będziemy budować przedział ufności dla wartości średniej 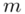 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 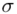 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 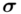 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 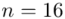 jest mniejsza od 30 (
jest mniejsza od 30 ( 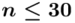 ), zatem wybieramy model II. Dysponujemy tabelą z danymi, więc możemy wyznaczyć z nich
), zatem wybieramy model II. Dysponujemy tabelą z danymi, więc możemy wyznaczyć z nich 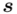 lub
lub 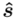 . Decyzja, którą opcję wybrać należy do nas, jest to właściwie obojętne, ale najczęściej wybiera się
. Decyzja, którą opcję wybrać należy do nas, jest to właściwie obojętne, ale najczęściej wybiera się 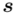 (o ile nie zostanie narzucone inaczej), także interesuje nas pierwsza wersja wzoru z wybranego modelu.
(o ile nie zostanie narzucone inaczej), także interesuje nas pierwsza wersja wzoru z wybranego modelu.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 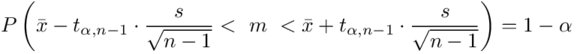 konkretnymi liczbami. Jak widać potrzebujemy średniej z próby
konkretnymi liczbami. Jak widać potrzebujemy średniej z próby 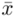 i odchylenia standardowego
i odchylenia standardowego 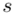 . W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
. W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej.
Dysponujemy danymi tabelarycznymi, gdzie warianty cechy (wiek pracowników) są w formie przedziałów tzn. od jednej wartości do drugiej wartości. Taki szereg określa się szeregiem rozdzielczym przedziałowym. Przeredagujmy zatem tabelę z zadania właśnie na tą postać szeregu.
|
(wiek pracowników) |
(liczba pracowników) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W przypadku szeregu rozdzielczego przedziałowego nie ma możliwości pomyłki do tego co jest wariantem cechy, a co liczebnością 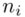 , ponieważ nie zdarza się, aby
, ponieważ nie zdarza się, aby 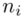 było zapisane w formie przedziałów. Symbol
było zapisane w formie przedziałów. Symbol 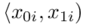 to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. W tabeli z zadania mamy właśnie przedstawioną sytuację
to po prostu ogólny zapis przedziału lewostronnie domkniętego i prawostronnie otwartego (chyba najczęściej używany – chociaż zależy od preferencji prowadzącego). Należy pilnować, aby końcówka każdego przedziału była początkiem następnego. W tabeli z zadania mamy właśnie przedstawioną sytuację  ,
,  (kończymy przedział na 24, następny również zaczynamy od 24), itd. w związku z tym nie musimy nic zmieniać, zachowana jest ciągłość.
(kończymy przedział na 24, następny również zaczynamy od 24), itd. w związku z tym nie musimy nic zmieniać, zachowana jest ciągłość.
W szeregu przedziałowym średnią liczymy ze wzoru 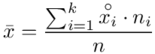 .
.
Na początku wyjaśnijmy symbol 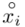 . Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły
. Oznacza on środek każdego z podanych przedziałów, a obliczany jest na podstawie formuły 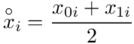 . Upraszczając należy zsumować początek
. Upraszczając należy zsumować początek 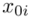 i koniec
i koniec 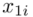 każdego przedziału i wynik podzielić na dwa.
każdego przedziału i wynik podzielić na dwa.
Wracamy do wzoru na średnią. Znak 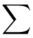 oznacza sumę. Pod tym symbolem znajduje się zapis
oznacza sumę. Pod tym symbolem znajduje się zapis 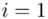 , a nad nim
, a nad nim 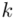 ,
, 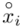 to środki kolejnych przedziałów, a
to środki kolejnych przedziałów, a 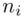 liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny
liczebności dla kolejnych przedziałów. Wszytko razem oznacza, że będziemy sumować kolejne iloczyny 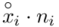 , gdzie
, gdzie 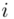 będzie rosło od
będzie rosło od 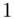 aż do wartości
aż do wartości 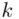 , a więc
, a więc 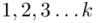 , a więc ogólnie:
, a więc ogólnie:
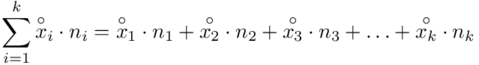
W naszym przypadku 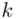 znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
znad znaku sumy oznacza liczbę przedziałów klasowych (ilość wierszy w tabeli z danymi). Tak więc średnia będzie miała uproszczony wzór:
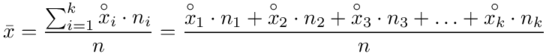
Czym jest 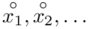 ,
, 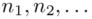 oraz
oraz 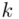 ? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
? Wszystko to zostanie pokazane dokładnie w tabeli. Obliczmy również środki poszczególnych przedziałów.
|
Numer klasy |
(wiek pracowników) |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uzupełniając 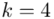 otrzymujemy wzór:
otrzymujemy wzór:
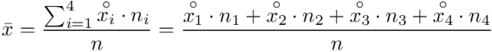 i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość
i oczywiście możemy uzupełnić go danymi z tabeli, ale proponuję nadal korzystać z tabeli i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na średnią z szeregu przedziałowego, a jej nagłówki zawsze wyglądają tak samo. Każdą wartość 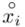 mnożymy przez odpowiadającą jej wartość
mnożymy przez odpowiadającą jej wartość 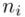 , a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem
, a następnie sumujemy powstałe iloczyny. Przecięcie wiersza z symbolem 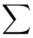 i kolumny
i kolumny 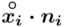 daje kompletny licznik wzoru na średnią.
daje kompletny licznik wzoru na średnią.
|
Numer klasy |
środki przedziałów |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
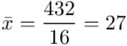
Zostało nam jeszcze odchylenie standardowe 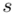 . Na początek i tak musimy obliczyć wariancję
. Na początek i tak musimy obliczyć wariancję 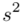 , bo
, bo 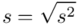 . Wzór na wariancję z danych szeregu przedziałowego wygląda następująco:
. Wzór na wariancję z danych szeregu przedziałowego wygląda następująco: 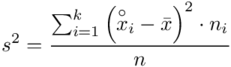 . Jest też alternatywa
. Jest też alternatywa 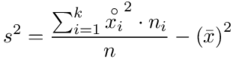 , ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
, ale będziemy używać pierwszej wersji. Rozpisanie wzoru analogiczne jak w przypadku średniej. Jak widać do policzenia wariancji i tak niezbędna jest średnia. Na początek ogólnie:
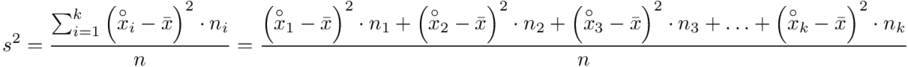
i dla ilości klas z zadania 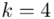 :
:
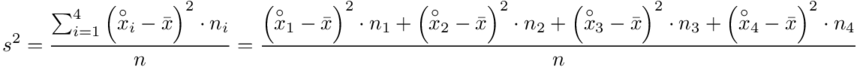
Tu też można podstawiać dane z tabeli, ale ponownie proponuję trzymać się obliczeń tabelarycznych. Można kontynuować poprzednią tabelę dopisując kolejne kolumny. Znowu krok po kroku będziemy tworzyć licznik ze wzoru. Dopisana pierwsza kolumna - od każdego środka przedziału 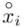 odejmujemy wcześniej wyliczoną średnią
odejmujemy wcześniej wyliczoną średnią 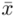 , druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości
, druga kolumna to podniesienie wyników z poprzedniej do kwadratu. Ostatnia to wymnożenie wyników z drugiej przez odpowiadające im wartości 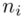 i dopiero ona jest sumowana (przecięcie wiersza z symbolem
i dopiero ona jest sumowana (przecięcie wiersza z symbolem 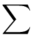 i
i 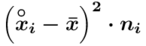 daje kompletny licznik wzoru na wariancję ).
daje kompletny licznik wzoru na wariancję ).
|
Numer klasy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
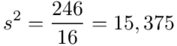
Odchylenie standardowe 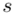 to pierwiastek z wariancji
to pierwiastek z wariancji 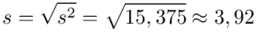 .
.
Wracamy do istoty zadania i wreszcie uzupełniamy wzór 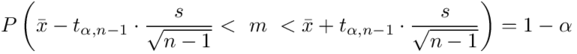 .
.
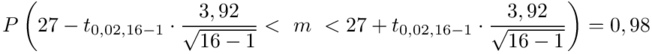
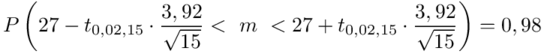
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t, zatem skorzystamy z tablic t-Studenta. Zapis 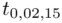 oznacza statystykę dla
oznacza statystykę dla 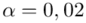 i 15 stopni swobody.
i 15 stopni swobody.
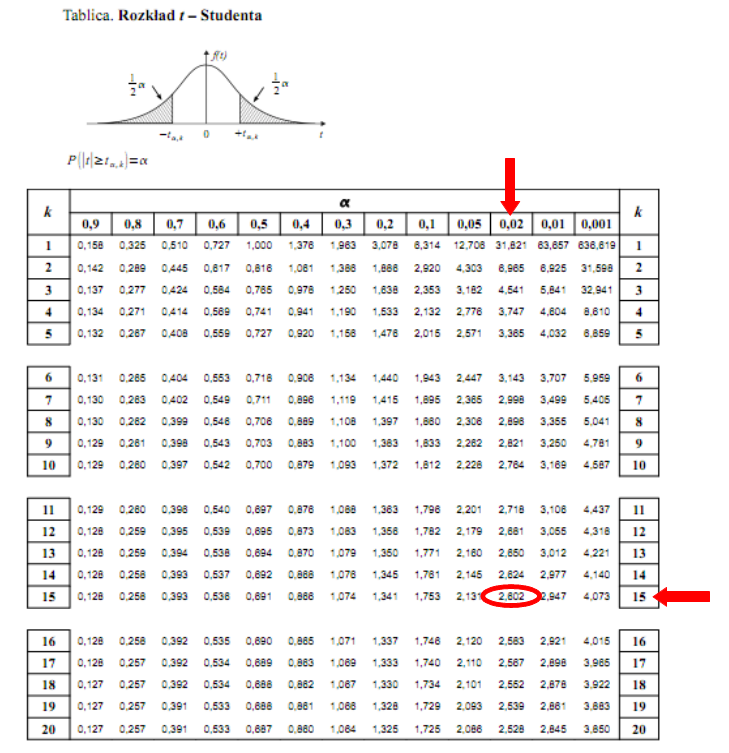
Wracamy do obliczeń i podstawiamy: 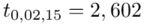
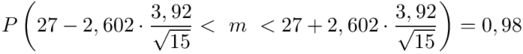
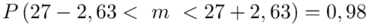
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy: 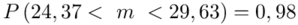 .
.
Interpretacja brzmi następująco:
Z ufnością 0,98 przeciętny wiek ogółu pracowników zakładu Z mieści się w przedziale od 24,37 lat do 29,63 lat.
Zadanie pochodzi z: Statystyka : elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka. Wyd. 6 popr., Wrocław : Wydawnictwo Akademii Ekonomicznej, 2006. - 455 s.: il.; 24 cm. ISBN 83-7011-783-X
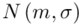 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 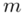 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 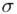
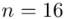
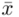 , wariancję
, wariancję 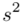 , odchylenie standardowe
, odchylenie standardowe 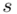 )
)
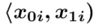 - warianty obserwacji
- warianty obserwacji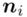 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych
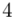

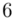

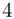

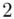
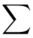 (suma)
(suma)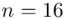
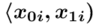 - przedziały klasowe
- przedziały klasowe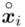 -
-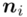 -liczebności poszczególnych przedziałów klasowych
-liczebności poszczególnych przedziałów klasowych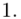

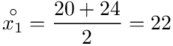
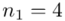
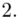

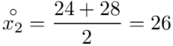
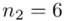

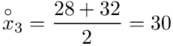
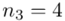
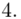

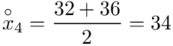
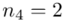
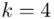
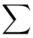 (suma)
(suma)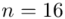
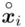 -
-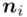 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych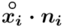
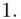
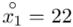
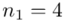
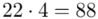
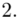
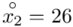
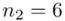
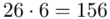
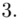
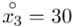
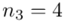
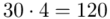
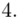
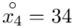
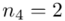
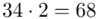
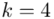
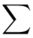 (suma)
(suma)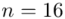
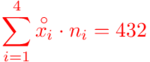
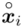 - środki przedziałów
- środki przedziałów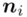 - liczebności poszczególnych przedziałów klasowych
- liczebności poszczególnych przedziałów klasowych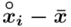
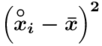
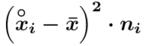
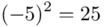
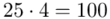
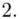
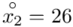
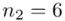
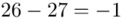
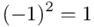
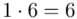
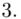
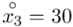
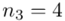
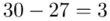
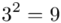
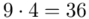
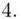
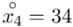
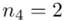
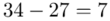
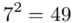
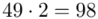
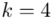
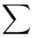 (suma)
(suma)