
Zadanie 37
Wytrzymałość pewnego materiału budowlanego (w kg/cm2) jest zmienną losową o rozkładzie 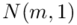 . W celu oszacowania nieznanej średniej wytrzymałości tego materiału dokonano pomiaru wytrzymałości 5 wylosowanych niezależnie sztuk tego materiału. Wyniki pomiarów były następujące: 20,4; 19,6; 22,1; 20,8; 21,1.
. W celu oszacowania nieznanej średniej wytrzymałości tego materiału dokonano pomiaru wytrzymałości 5 wylosowanych niezależnie sztuk tego materiału. Wyniki pomiarów były następujące: 20,4; 19,6; 22,1; 20,8; 21,1.
1. Przyjmując współczynnik ufności 0,90, zbudować przedział ufności dla średniej wytrzymałości badanego materiału budowlanego.
2. O ile zmieni się długość oszacowanego przedziału, jeśli liczebność próby zwiększymy do 45 elementów?
3. Jak zmieni się precyzja oszacowania, jeśli wielkość współczynnika ufności zwiększymy do 0,95?
W celu zachowania przejrzystości każdy z podpunktów będzie wykonany oddzielnie.
Ad. 1
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na zdanie:
„Przyjmując współczynnik ufności 0,90, zbudować przedział ufności dla średniej wytrzymałości badanego materiału budowlanego.”
Mamy tu zwroty: zbudować przedział ufności i współczynnik ufności- w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Wytrzymałość pewnego materiału budowlanego (w kg/cm2) jest zmienną losową o rozkładzie 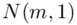 .”
.”
Dowiadujemy się, że wytrzymałość pewnego materiału budowlanego jest cechą o rozkładzie normalnym i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Ponadto możemy odczytać jeden z parametrów rozkładu 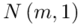 tzn. odchylenie standardowe dla populacji
tzn. odchylenie standardowe dla populacji 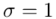 i ostatecznie zapisać jako rozkład normalny o nieznanej średniej
i ostatecznie zapisać jako rozkład normalny o nieznanej średniej 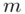 i znanym odchyleniu standardowym
i znanym odchyleniu standardowym 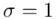 .
.
„W celu oszacowania nieznanej średniej wytrzymałości tego materiału dokonano pomiaru wytrzymałości 5 wylosowanych niezależnie sztuk tego materiału.”
W tym momencie wiemy, że wybrano próbę, a jej liczebność to 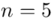 i w związku z tym będziemy stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji. Podano również informacje o konkretnych wynikach z próby. Jeżeli dysponujemy wartościami wypisanymi po przecinku tzw. danymi indywidualnymi, to zawsze możemy policzyć średnią
i w związku z tym będziemy stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji. Podano również informacje o konkretnych wynikach z próby. Jeżeli dysponujemy wartościami wypisanymi po przecinku tzw. danymi indywidualnymi, to zawsze możemy policzyć średnią 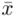 , wariancję
, wariancję 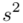 i odchylenie standardowe
i odchylenie standardowe 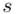 (lub
(lub 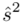 ,
, 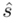 ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
„Przyjmując współczynnik ufności 0,90, zbudować przedział ufności dla średniej wytrzymałości badanego materiału budowlanego.”
Na końcu podano współczynnik ufności 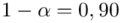 . Od razu wyznaczamy
. Od razu wyznaczamy 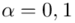 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA materiał budowlany |
PRÓBA 5 wybranych sztuk materiału budowlanego |
|
|
|
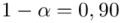 - współczynnik ufności,
- współczynnik ufności, 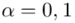
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:
„Przyjmując współczynnik ufności 0,90, zbudować przedział ufności dla średniej wytrzymałości badanego materiału budowlanego.”
Wyrażenie średniej oznacza, że będziemy budować przedział ufności dla wartości średniej 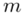 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 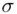 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 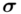 jest znana
jest znana 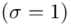 i tylko model I jest odpowiedni. Liczebność próby nie jest w ogóle istotna.
i tylko model I jest odpowiedni. Liczebność próby nie jest w ogóle istotna.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 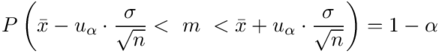 konkretnymi liczbami. Jak widać potrzebujemy średniej z próby
konkretnymi liczbami. Jak widać potrzebujemy średniej z próby 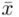 . W związku z tym, zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć (na razie) nieznany parametr. Liczenie średniej jest zagadnieniem ze statystyki opisowej. Dysponujemy danymi indywidualnymi (wypisanymi po przecinku), jest ich niewiele i nie powtarzają się - zatem średnią liczymy ze wzoru
. W związku z tym, zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć (na razie) nieznany parametr. Liczenie średniej jest zagadnieniem ze statystyki opisowej. Dysponujemy danymi indywidualnymi (wypisanymi po przecinku), jest ich niewiele i nie powtarzają się - zatem średnią liczymy ze wzoru 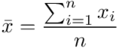 . Oczywiście na chłopski rozum średnią można policzyć sumując wszystkie dane, a potem dzieląc przez ilość – i jest to jak najbardziej prawidłowe rozwiązanie, a ten wzór oznacza to samo. Jednak zdaję sobie sprawę, że widząc „hieroglify” tego typu wiele osób nie wie co robić, a tym bardziej jak je rozpisywać :). Mając to na uwadze postaram się przybliżyć kwestię wzorów rozpisując je na czynniki pierwsze.
. Oczywiście na chłopski rozum średnią można policzyć sumując wszystkie dane, a potem dzieląc przez ilość – i jest to jak najbardziej prawidłowe rozwiązanie, a ten wzór oznacza to samo. Jednak zdaję sobie sprawę, że widząc „hieroglify” tego typu wiele osób nie wie co robić, a tym bardziej jak je rozpisywać :). Mając to na uwadze postaram się przybliżyć kwestię wzorów rozpisując je na czynniki pierwsze.
Znak 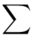 oznacza sumę. Pod tym symbolem znajduje się zapis
oznacza sumę. Pod tym symbolem znajduje się zapis 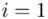 , a nad nim
, a nad nim 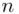 ,
, 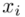 to wartości kolejnych obserwacji. Wszytko razem oznacza, że będziemy sumować kolejne obserwacje oznaczone symbolem
to wartości kolejnych obserwacji. Wszytko razem oznacza, że będziemy sumować kolejne obserwacje oznaczone symbolem 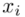 , gdzie
, gdzie 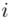 będzie rosło od
będzie rosło od 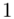 aż do wartości
aż do wartości 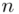 , a więc
, a więc 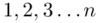 .
.
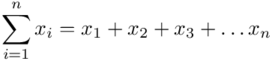
Tak więc średnia będzie miała uproszczony wzór:
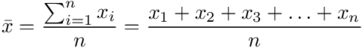
Teraz przełożymy wszystko na dane z zadania. Liczebność próby wynosi 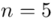 , a więc wzór na średnią możemy zapisać następująco:
, a więc wzór na średnią możemy zapisać następująco:
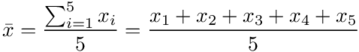
Czym jest 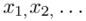 ? To są konkretne wyniki z próby, a więc
? To są konkretne wyniki z próby, a więc 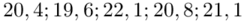 . Jeśli ktoś chciałby uporządkować dane indywidualne od najmniejszej do największej, może to spokojnie zrobić. Porządkowanie liczb nie wpływa na wynik, także może zostać tak jak jest. A więc
. Jeśli ktoś chciałby uporządkować dane indywidualne od najmniejszej do największej, może to spokojnie zrobić. Porządkowanie liczb nie wpływa na wynik, także może zostać tak jak jest. A więc 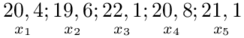 .
.
Obliczamy średnią:
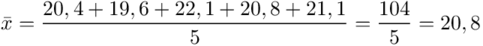
Wracamy do istoty zadania i wreszcie uzupełniamy wzór 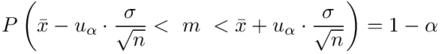 :
:
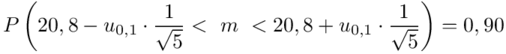
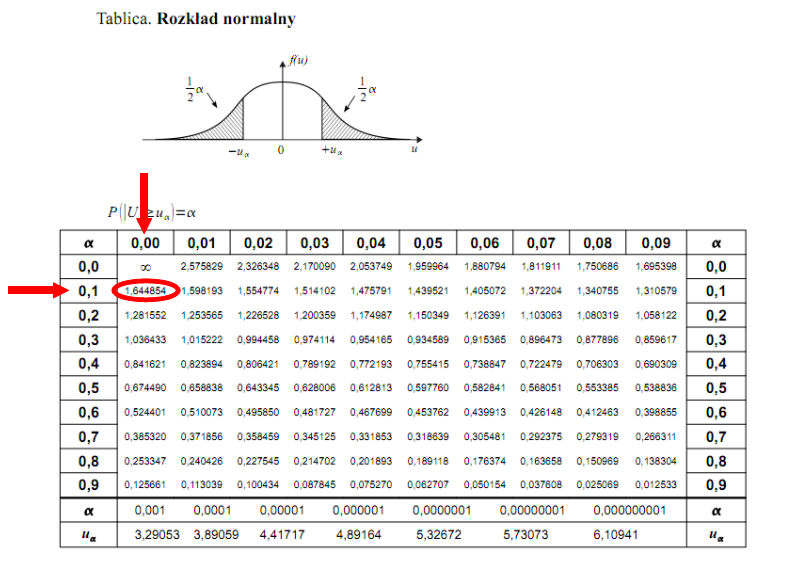
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka u, zatem skorzystamy z tablic rozkładu normalnego. Zapis 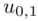 oznacza konieczność odnalezienia statystyki dla
oznacza konieczność odnalezienia statystyki dla 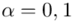 .
.
Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku 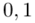 sumujemy
sumujemy 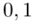 i
i 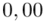 czyli
czyli 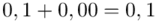 .
.
Wracamy do obliczeń i podstawiamy 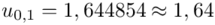 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego)
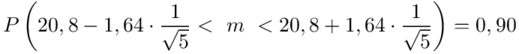
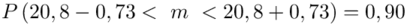
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy: 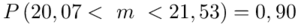 .
.
Interpretacja brzmi następująco:
Z ufnością 0,90 średnia wytrzymałość badanego materiału budowlanego mieści się w przedziale od 20,07 kg/cm2 do 21,53 kg/cm2.
Ad. 2
Na początku ustalimy przedział ufności dla liczebności próby 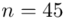 elementów. Zakładamy, że reszta danych nie ulega zmianie i nadal budujemy przedział ufności dla średniej
elementów. Zakładamy, że reszta danych nie ulega zmianie i nadal budujemy przedział ufności dla średniej 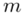 . Sprawdźmy zatem, czy wzór na estymację pozostanie bez zmian. Nadal znamy
. Sprawdźmy zatem, czy wzór na estymację pozostanie bez zmian. Nadal znamy 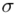 , ponieważ
, ponieważ 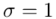 , więc pozostajemy przy formule z modelu I:
, więc pozostajemy przy formule z modelu I: 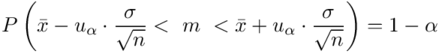 , liczebność próby nie wpływa na wybór.
, liczebność próby nie wpływa na wybór.
Uzupełniamy wybrany wzór:
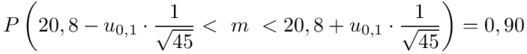
również wartość statystyki 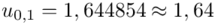 odczytana w poprzednim podpunkcie nie ulega zmianie.
odczytana w poprzednim podpunkcie nie ulega zmianie.
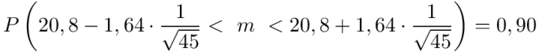
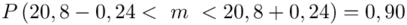
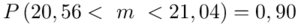
Znamy już przedział po zmianie liczebności próby, ale pytanie w zadaniu dotyczy zmiany długości przedziału.
Na początek przypomnienie na zwykłych liczbach. Weźmy przykładowo przedział 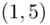 i naszkicujmy go na osi.
i naszkicujmy go na osi.
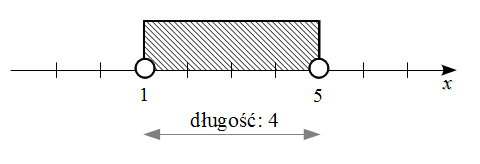
Aby obliczyć długość przedziału należy od końcówki odjąć jego początek, a więc 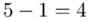 .
.
Teraz policzmy długość przedziału z podpunktu pierwszego dla 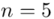 , czyli
, czyli 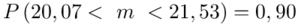 :
:
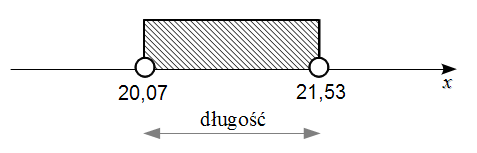
Długość przed zmianą: 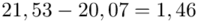
Analogicznie długość przedziału po zmianie liczebności próby do 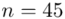 , czyli
, czyli 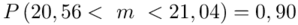 :
:
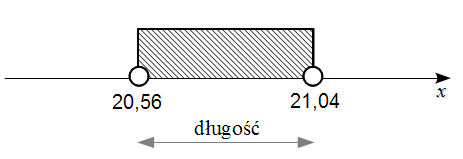
Długość po zmianie: 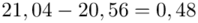
Ja widać długość przedziału uległa skróceniu z 1,46 do 0,48, a to oznacza 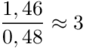 , że 3-krotnie.
, że 3-krotnie.
Ad. 3
Na początku ustalimy precyzję oszacowania dla poziomu ufności 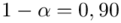 . Aby porównać precyzję oszacowania po zmianie poziomu ufności do poziomu
. Aby porównać precyzję oszacowania po zmianie poziomu ufności do poziomu 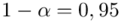 próby najlepiej posłużyć się względną precyzją szacunku, ponieważ porównywanie wielkości wyrażonych w procentach jest najbezpieczniejsze.
próby najlepiej posłużyć się względną precyzją szacunku, ponieważ porównywanie wielkości wyrażonych w procentach jest najbezpieczniejsze.
Względną precyzję oszacowania wartości oczekiwanej 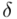 określamy wzorem:
określamy wzorem: 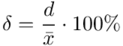 , gdzie
, gdzie 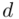 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej 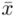 , a w związku z tym, że wybraliśmy w pierwszym podpunkcie dla
, a w związku z tym, że wybraliśmy w pierwszym podpunkcie dla 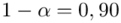 formułę na estymację średniej: ,
formułę na estymację średniej: , 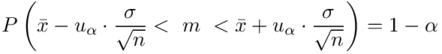 to
to 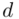 wygląda tak:
wygląda tak:
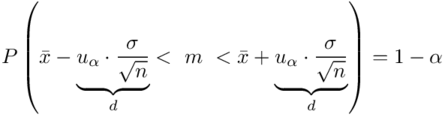
czyli 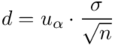 . Powtarzam jeszcze raz, że formuła na obliczenie
. Powtarzam jeszcze raz, że formuła na obliczenie 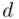 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej 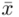 .
.
Uzupełniamy wzór:
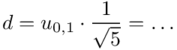
Uzupełniamy odczytane wcześniej 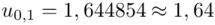
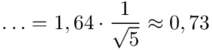 .
.
I względny błąd szacunku 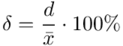 , czyli:
, czyli: 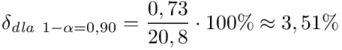 .
.
Teraz policzmy względną precyzję szacunku dla 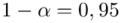 -
- 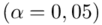 . Musimy się jednak upewnić, czy wzór na bezwzględny błąd szacunku
. Musimy się jednak upewnić, czy wzór na bezwzględny błąd szacunku 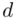 nie ulegnie zmianie. Na wybór formuły dotyczącej estymacji ma wpływ jedynie znajomość
nie ulegnie zmianie. Na wybór formuły dotyczącej estymacji ma wpływ jedynie znajomość 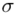 i ewentualnie liczebność próby – a to pozostało bez zmian. Wybór innego współczynnika ufności nie wpływa na wybór wzoru, a więc pozostajemy przy
i ewentualnie liczebność próby – a to pozostało bez zmian. Wybór innego współczynnika ufności nie wpływa na wybór wzoru, a więc pozostajemy przy 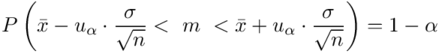 i
i 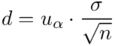 .
.
Obliczamy 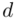 :
:
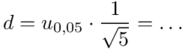
Symbol u oznacza konieczność odczytania odpowiedniej statystyki z tablic rozkładu normalnego.
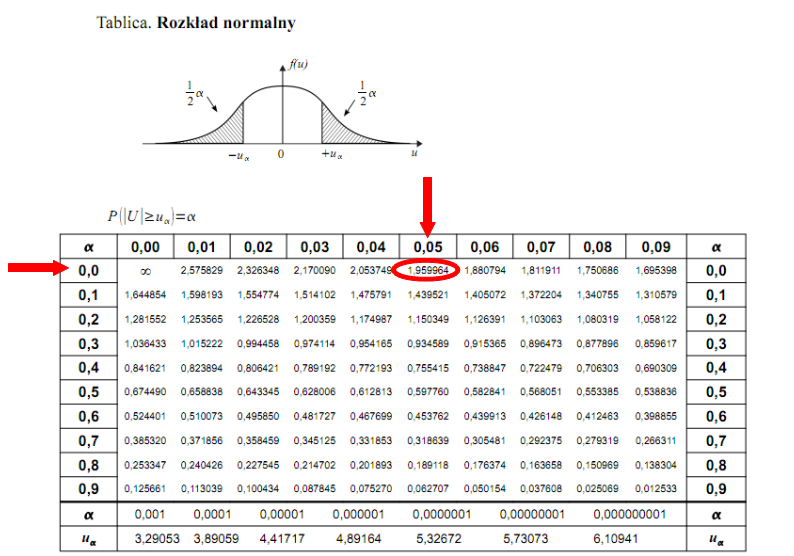
Czytanie z tablic rozkładu normalnego nie jest trudne. Sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. W przypadku 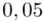 sumujemy
sumujemy 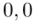 i
i 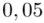 czyli
czyli 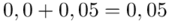 .
.
Wracamy do obliczeń i podstawiamy 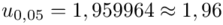 (zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
(zaokrąglanie to indywidualna sprawa wynikająca najczęściej z preferencji prowadzącego):
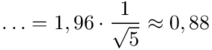
I względny błąd szacunku 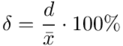 , czyli:
, czyli: 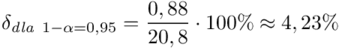 .
.
Precyzja oszacowania zmalała o 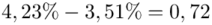 punktu procentowego lub jeśli ktoś się uprze może policzyć o ile procent wzrósł bezwzględny błąd szacunku
punktu procentowego lub jeśli ktoś się uprze może policzyć o ile procent wzrósł bezwzględny błąd szacunku 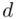 (od 19,5% do 20,5% w zależności od zaokrąglania). Coś tu jednak się nie zgadza, prawda? Przecież po zwiększeniu współczynnika ufności z 0,90 do 0,95 otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu. Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość
(od 19,5% do 20,5% w zależności od zaokrąglania). Coś tu jednak się nie zgadza, prawda? Przecież po zwiększeniu współczynnika ufności z 0,90 do 0,95 otrzymaliśmy większą liczbę i na chłopski rozum względna precyzja uległa zwiększeniu. Z względną precyzją szacunku jest tak, że im większa wartość liczbowa otrzymana w wyniku tym gorsza precyzja oszacowania. Jeśli interpretuje się względną precyzję szacunku to wartość 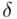 poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku
poniżej 5% mówi nam, że wnioskowanie o parametrze (w tym przypadku 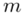 ) jest uprawnione i całkowicie bezpieczne, jeżeli
) jest uprawnione i całkowicie bezpieczne, jeżeli 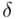 mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli
mieści się od 5% do 10% wnioskowanie jest możliwe, ale z zalecaną ostrożnością, a jeśli 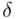 przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku
przekracza 10% wnioskowanie jest niewiarygodne i należy je przerwać. Uzyskiwanie niezadowalającej (powyżej 5%, a tym bardziej powyżej 10%) względnej precyzji szacunku 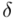 może być spowodowane zbyt wysokim współczynnikiem ufności, zbyt małą liczebnością próby oraz wysokim zróżnicowaniem wyników w próbie (np. duży rozstrzał danych).
może być spowodowane zbyt wysokim współczynnikiem ufności, zbyt małą liczebnością próby oraz wysokim zróżnicowaniem wyników w próbie (np. duży rozstrzał danych).
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4
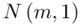 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 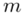 i odchyleniu standardowym
i odchyleniu standardowym 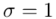
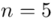
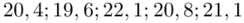 - dane indywidualne (można obliczyć średnią
- dane indywidualne (można obliczyć średnią 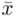 , wariancję
, wariancję 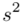 , odchylenie standardowe
, odchylenie standardowe  )
)