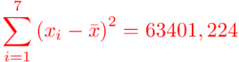Zadanie 33
Z dużej dostawy węgla kamiennego pobrano 7 jednokilogramowych próbek i określono ich wartość opałową. Otrzymano następujące wyniki (w kcal/1 kg spalonego węgla): 7220; 7530; 7450; 7322; 7286; 7352; 7406. Zakładając, że ilość kcal powstająca przy spalaniu węgla ma rozkład normalny, zbudować przedział ufności Neymana dla średniej wartości ciepła spalania węgla kamiennego. Przyjąć współczynnik ufności 0,90.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu zadania zwracamy uwagę na zdania:
„Zakładając, że ilość kcal powstająca przy spalaniu węgla ma rozkład normalny, zbudować przedział ufności Neymana dla średniej wartości ciepła spalania węgla kamiennego. Przyjąć współczynnik ufności 0,90. ”
Odnajdujemy w nich zwroty: zbudować przedział ufności Neymana i współczynnik ufności. Teraz mamy pewność, że zadanie dotyczy estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Z dużej dostawy węgla kamiennego pobrano 7 jednokilogramowych próbek i określono ich wartość opałową.”
W tym momencie wiemy, że wylosowaliśmy próbę, a jej liczebność to 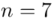 i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
i w związku z tym będziemy prawdopodobnie stosować oznaczenia parametrów dla próby, chyba że zostanie wyraźnie określone, że będą to parametry dla populacji.
„Otrzymano następujące wyniki (w kcal/1 kg spalonego węgla): 7220; 7530; 7450; 7322; 7286; 7352; 7406.”
Podano informacje o konkretnych wynikach z próby. Jeżeli dysponujemy wartościami wypisanymi po przecinku tzw. danymi indywidualnymi, to zawsze możemy policzyć średnią 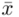 , wariancję
, wariancję 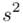 i odchylenie standardowe
i odchylenie standardowe 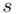 (lub
(lub 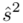 ,
, 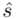 ). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
). Nie liczmy jednak tych parametrów od razu, ponieważ dopiero etap wyboru formuły na estymację wskaże nam czego potrzebujemy. Po prostu chodzi o to, żeby nie liczyć na zapas np. odchylenia, bo może okazać się niepotrzebne w późniejszych obliczeniach.
„Zakładając, że ilość kcal powstająca przy spalaniu węgla ma rozkład normalny, zbudować przedział ufności Neymana dla średniej wartości ciepła spalania węgla kamiennego. ”
W zadaniu występuje założenie normalności rozkładu ilości kcal i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Nie mamy informacji na temat tego rozkładu, zatem możemy tylko zapisać 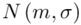 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 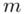 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 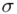 .
.
„Przyjąć współczynnik ufności 0,90. „
Podano też współczynnik ufności 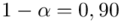 . Od razu wyznaczamy
. Od razu wyznaczamy 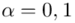 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA dostawa węgla kamiennego |
PRÓBA 7 wybranych jednokilogramowych próbek |
|
|
|
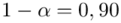 - współczynnik ufności,
- współczynnik ufności, 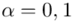
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i w przedostatnim zdaniu wyłapujemy słowo:
„Zakładając, że ilość kcal powstająca przy spalaniu węgla ma rozkład normalny, zbudować przedział ufności Neymana dla średniej wartości ciepła spalania węgla kamiennego.”
Wyraz średniej oznacza, że będziemy budować przedział ufności dla wartości średniej 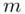 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 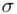 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 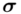 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 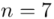 jest mniejsza od 30 (
jest mniejsza od 30 ( 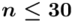 ), zatem wybieramy model II. Dysponujemy danymi indywidualnymi, więc możemy wyznaczyć z nich
), zatem wybieramy model II. Dysponujemy danymi indywidualnymi, więc możemy wyznaczyć z nich 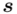 lub
lub 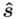 . Decyzja, którą opcję wybrać należy do nas, jest to właściwie obojętne, ale najczęściej wybiera się
. Decyzja, którą opcję wybrać należy do nas, jest to właściwie obojętne, ale najczęściej wybiera się 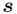 (o ile nie zostanie narzucone inaczej), także interesuje nas pierwsza wersja wzoru z wybranego modelu.
(o ile nie zostanie narzucone inaczej), także interesuje nas pierwsza wersja wzoru z wybranego modelu.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 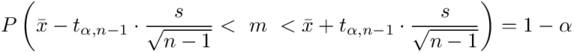 konkretnymi liczbami. Jak widać potrzebujemy średniej z próby
konkretnymi liczbami. Jak widać potrzebujemy średniej z próby 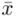 i odchylenia standardowego
i odchylenia standardowego 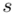 . W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej. Dysponujemy danymi indywidualnymi (wypisanymi po przecinku), jest ich niewiele i nie powtarzają się - zatem średnią liczymy ze wzoru
. W związku z tym zanim zajmiemy się uzupełnianiem właściwego wzoru należy obliczyć dwa (na razie) nieznane parametry. Liczenie średniej, wariacji i odchylenia standardowego jest zagadnieniem ze statystyki opisowej. Dysponujemy danymi indywidualnymi (wypisanymi po przecinku), jest ich niewiele i nie powtarzają się - zatem średnią liczymy ze wzoru 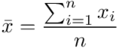 . Oczywiście na chłopski rozum średnią można policzyć sumując wszystkie dane, a potem dzieląc przez ilość – i jest to jak najbardziej prawidłowe rozwiązanie, a ten wzór oznacza to samo. Jednak zdaję sobie sprawę, że widząc „hieroglify” tego typu wiele osób nie wie co robić, a tym bardziej jak je rozpisywać :). Mając to na uwadze postaram się przybliżyć kwestię wzorów rozpisując je na czynniki pierwsze.
. Oczywiście na chłopski rozum średnią można policzyć sumując wszystkie dane, a potem dzieląc przez ilość – i jest to jak najbardziej prawidłowe rozwiązanie, a ten wzór oznacza to samo. Jednak zdaję sobie sprawę, że widząc „hieroglify” tego typu wiele osób nie wie co robić, a tym bardziej jak je rozpisywać :). Mając to na uwadze postaram się przybliżyć kwestię wzorów rozpisując je na czynniki pierwsze.
Znak 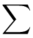 oznacza sumę. Pod tym symbolem znajduje się zapis
oznacza sumę. Pod tym symbolem znajduje się zapis 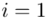 , a nad nim
, a nad nim 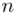 ,
, 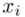 to wartości kolejnych obserwacji. Wszytko razem oznacza, że będziemy sumować kolejne obserwacje oznaczone symbolem
to wartości kolejnych obserwacji. Wszytko razem oznacza, że będziemy sumować kolejne obserwacje oznaczone symbolem 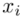 , gdzie
, gdzie 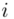 będzie rosło od
będzie rosło od 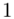 aż do wartości
aż do wartości 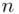 , a więc
, a więc 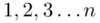 .
.
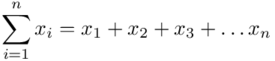
Tak więc średnia będzie miała uproszczony wzór:
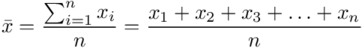
Teraz przełożymy wszystko na dane z zadania. Liczebność próby wynosi 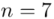 , a więc wzór na średnią możemy zapisać następująco:
, a więc wzór na średnią możemy zapisać następująco:
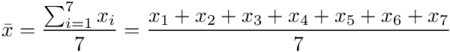
Czym jest 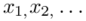 ? To są konkretne wyniki z próby, a więc
? To są konkretne wyniki z próby, a więc 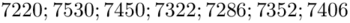 . Jeśli ktoś chciałby uporządkować dane indywidualne od najmniejszej do największej, może to spokojnie zrobić. Porządkowanie liczb nie wpływa na wynik, także może zostać tak jak jest. A więc
. Jeśli ktoś chciałby uporządkować dane indywidualne od najmniejszej do największej, może to spokojnie zrobić. Porządkowanie liczb nie wpływa na wynik, także może zostać tak jak jest. A więc 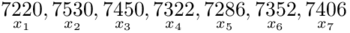 .
.
Obliczamy średnią:
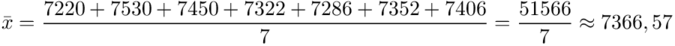
Zostało nam jeszcze odchylenie standardowe 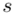 . Na początek i tak musimy obliczyć wariancję
. Na początek i tak musimy obliczyć wariancję 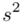 , bo
, bo 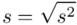 . Wzór na wariancję z danych indywidualnych wygląda tak:
. Wzór na wariancję z danych indywidualnych wygląda tak: 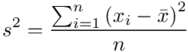 . Jest też alternatywa
. Jest też alternatywa 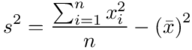 , ale będziemy używać pierwszej wersji. Rozpisanie wzoru będzie analogiczne jak w przypadku średniej. Na początek ogólnie:
, ale będziemy używać pierwszej wersji. Rozpisanie wzoru będzie analogiczne jak w przypadku średniej. Na początek ogólnie:
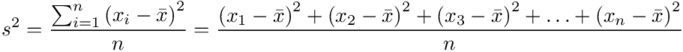
i dla 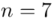 :
:
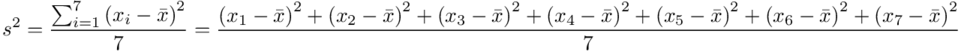
Jak widać do policzenia wariancji i tak niezbędna jest średnia.
Możemy już podstawiać liczby za 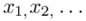 , ale proponuję utworzyć tabelkę i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na wariancję z danych indywidualnych, a jej nagłówki zawsze wyglądają tak samo. Na początku od każdego wartości
, ale proponuję utworzyć tabelkę i wykonywać w niej obliczenia. Po pierwsze jest bardziej klarowna, po drugie ułamek powstały po rozpisaniu wzoru może okazać się dłuższym tasiemcem niż w tym konkretnym zadaniu i łatwo tu o pomyłkę. W tabelce powoli budujemy wzór na wariancję z danych indywidualnych, a jej nagłówki zawsze wyglądają tak samo. Na początku od każdego wartości 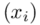 odejmujemy średnią, a następnie wynik podnosimy do kwadratu. Sumujemy ostatnią kolumnę (przecięcie wiersza z symbolem
odejmujemy średnią, a następnie wynik podnosimy do kwadratu. Sumujemy ostatnią kolumnę (przecięcie wiersza z symbolem 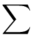 i
i  daje kompletny licznik wzoru na wariancję )
daje kompletny licznik wzoru na wariancję )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
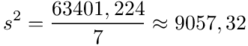
Odchylenie standardowe 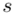 to pierwiastek z wariancji
to pierwiastek z wariancji 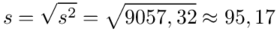 .
.
Wracamy do istoty zadania i wreszcie uzupełniamy wzór 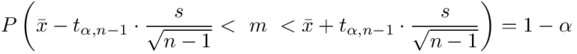 .
.
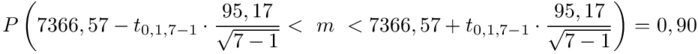
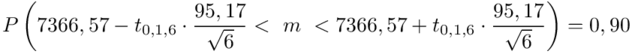
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t, zatem skorzystamy z tablic t-Studenta. Zapis 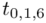 oznacza statystykę dla
oznacza statystykę dla 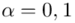 i 6 stopni swobody.
i 6 stopni swobody.
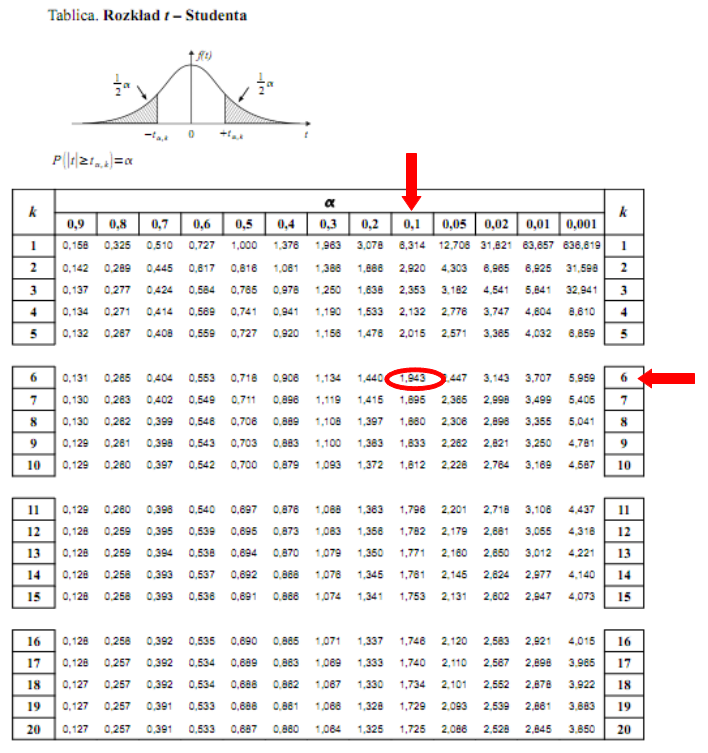
Wracamy do obliczeń i podstawiamy 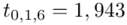 :
:
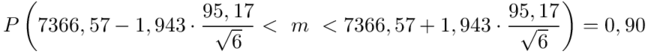
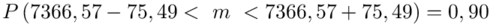
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy: . 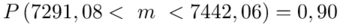
Interpretacja brzmi następująco:
Z ufnością 0,90 średnia wartości ciepła spalania węgla kamiennego mieści się w przedziale od 7291,08 kcal do 7442,06 kcal.
Statystyka: podstawy teoretyczne, przykłady, zadania / Mieczysław Sobczyk. - Wyd.1 - Lublin : Wydaw.Uniw.M.Curie-Skłodowskiej, 2000 - 425 s. ; 25 cm. - ISBN 83-227-1608-7
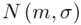 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 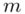 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 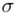
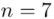
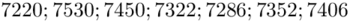 – dane indywidualne (można obliczyć średnią
– dane indywidualne (można obliczyć średnią 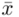 , wariancję
, wariancję 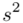 , odchylenie standardowe
, odchylenie standardowe 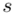 )
)
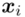
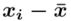

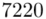
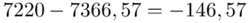
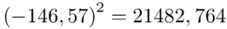
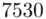
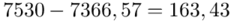
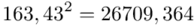
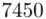
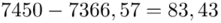
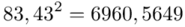
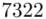
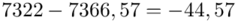
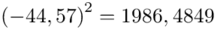
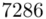
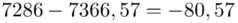
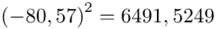
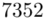
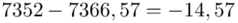
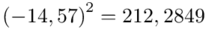
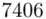
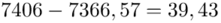
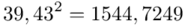
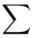 (suma)
(suma)