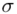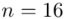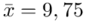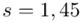Zadanie 23
Zakładamy, że roczne zużycie proszku do prania na osobę w rodzinach czteroosobowych jest zmienną losową o rozkładzie 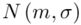 . Oszacować metodą przedziałową przeciętne roczne zużycie proszku, na poziomie ufności 0,95, jeśli na podstawie 16-elementowej próby prostej, pobranej ze zbiorowości czteroosobowych gospodarstw domowych, otrzymano: średnie roczne zużycie
. Oszacować metodą przedziałową przeciętne roczne zużycie proszku, na poziomie ufności 0,95, jeśli na podstawie 16-elementowej próby prostej, pobranej ze zbiorowości czteroosobowych gospodarstw domowych, otrzymano: średnie roczne zużycie 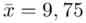 kg i odchylenie standardowe
kg i odchylenie standardowe 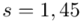 kg. Jaki jest względny błąd szacunku?
kg. Jaki jest względny błąd szacunku?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Zwracamy uwagę na zdanie:
„Oszacować metodą przedziałową przeciętne roczne zużycie proszku, na poziomie ufności 0,95...”
Odnajdujemy w nim zwrot: oszacować metodą przedziałową. Występuje też wyrażenie poziom ufności – w związku z tym z całą pewnością zadanie dotyczy estymacji przedziałowej. Formuła na względny błąd szacunku zostanie określona na etapie wyboru wzoru na estymację.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Zakładamy, że roczne zużycie proszku do prania na osobę w rodzinach czteroosobowych jest zmienną losową o rozkładzie 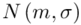 . ”
. ”
Wiemy, że rozkład zużycia proszku do prania jest normalny i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Nic nie wiemy na temat tego rozkładu, zatem możemy tylko zapisać tak jak w treści zadania: 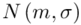 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 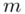 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 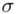 .
.
„Oszacować metodą przedziałową przeciętne roczne zużycie proszku, na poziomie ufności 0,95, jeśli na podstawie 16-elementowej próby prostej, pobranej ze zbiorowości czteroosobowych gospodarstw domowych, otrzymano: średnie roczne zużycie 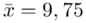 kg i odchylenie standardowe
kg i odchylenie standardowe 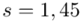 kg.”
kg.”
Podano poziom ufności 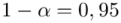 , od razu wyznaczamy
, od razu wyznaczamy 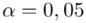 . W tym momencie wiemy, że wylosowaliśmy próbę, a jej liczebność to
. W tym momencie wiemy, że wylosowaliśmy próbę, a jej liczebność to 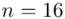 . Określona jest średnia i odchylenie standardowe z próby, nie mamy wątpliwości co do oznaczeń, więc po prostu spisujemy
. Określona jest średnia i odchylenie standardowe z próby, nie mamy wątpliwości co do oznaczeń, więc po prostu spisujemy 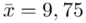 i
i 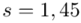 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA zbiorowość czteroosobowych gospodarstw domowych |
PRÓBA 16 wybranych gospodarstw |
|
|
|
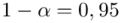 - współczynnik ufności,
- współczynnik ufności, 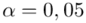
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który należy oszacować przedziałem ufności i wyłapujemy słowo:
„Oszacować metodą przedziałową przeciętne roczne zużycie proszku, na poziomie ufności 0,95...”
Wyraz przeciętne oznacza, że będziemy budować przedział ufności dla wartości średniej 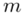 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 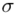 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 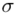 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 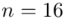 jest mniejsza od 30 (
jest mniejsza od 30 ( 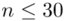 ), zatem wybieramy model II. W danych występuje
), zatem wybieramy model II. W danych występuje 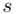 , także interesuje nas pierwsza wersja wzoru z wybranego modelu.
, także interesuje nas pierwsza wersja wzoru z wybranego modelu.

Nadszedł czas by określić wzór na względną precyzję oszacowania wartości oczekiwanej 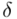 .
.
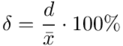 , gdzie
, gdzie 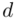 (bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej
(bezwzględny błąd szacunku) jest wielkością odejmowaną i dodawaną do średniej 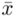 :
:
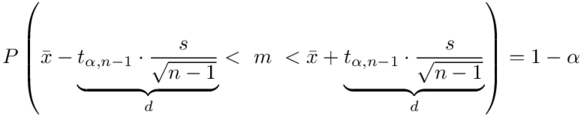
czyli 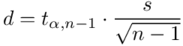 . Powtarzam jeszcze raz, że formuła na obliczenie
. Powtarzam jeszcze raz, że formuła na obliczenie 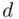 zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej
zależy od wzoru wybranego na przedział ufności, ale zawsze jest to wielkość odejmowana i dodawana do średniej 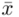 .
.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 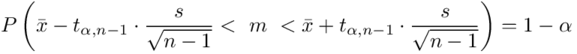 konkretnymi liczbami.
konkretnymi liczbami.
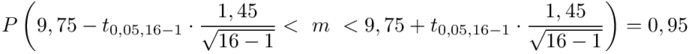
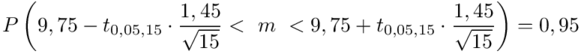
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka t, zatem skorzystamy z tablic t-Studenta. Zapis 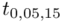 oznacza statystykę dla
oznacza statystykę dla 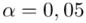 i 15 stopni swobody.
i 15 stopni swobody.
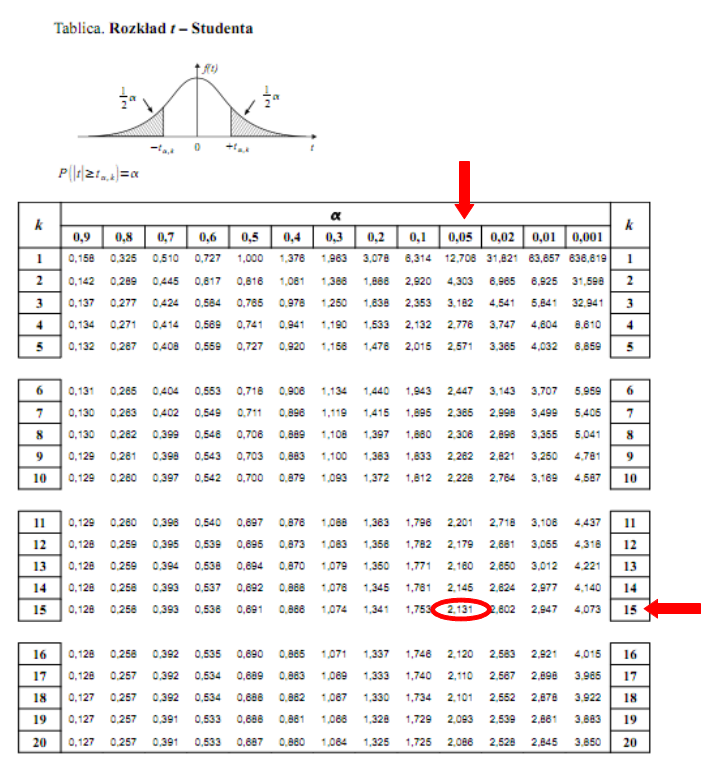
Wracamy do obliczeń i podstawiamy: 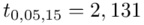
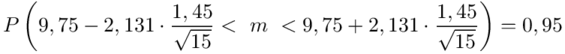
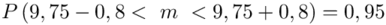
Z kolei względna precyzja szacunku:
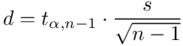
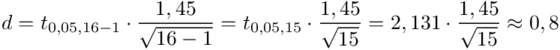
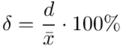
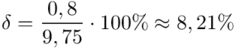
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy: 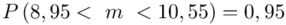 .
.
Interpretacja brzmi następująco:
Z ufnością 0,95 przeciętne roczne zużycie proszku mieści się w przedziale od 8,95 kg do 10,55 kg. Względny błąd szacunku wynosi 8,21%.
Zadanie pochodzi z: Statystyka : elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka. Wyd. 6 popr., Wrocław : Wydawnictwo Akademii Ekonomicznej, 2006. - 455 s.: il.; 24 cm. ISBN 83-7011-783-X
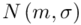 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 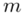 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym