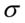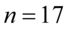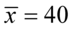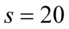Zadanie 18
Na podstawie wielokrotnych obserwacji ustalono, że rozkład wieku osób pracowników umysłowych w przemyśle ciężkim jest rozkładem normalnym. W celu oszacowania nieznanej wartości średniej w tym rozkładzie wylosowano niezależnie 17-elementową próbę pracowników. Średni wiek w tej próbie wynosił 40 lat, a odchylenie standardowe stanowiło 0,5 czasu średniego. Jaki współczynnik ufności przyjęto przy szacowaniu średniej w rozkładzie wieku ogółu pracowników, jeżeli długość oszacowanego przedziału wynosiła 21,21 lat?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Po przeczytaniu całego zadania zwracamy uwagę na ostatnie zdanie:
„Jaki współczynnik ufności przyjęto przy szacowaniu średniej w rozkładzie wieku ogółu pracowników, jeżeli długość oszacowanego przedziału wynosiła 21,21 lat?”
Odnajdujemy zwrot: oszacowanego przedziału, dodatkowo występuje wyrażenie: współczynnik ufności i w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.
Z treści zadania wynika, że nie trzeba obliczać końcówek przedziału ufności, a szukany jest współczynnik ufności 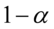 z reguły występujący w danych, zatem określimy to zadanie nieco kolokwialnie - „od tyłu”. Zresztą podano długość przedziału ufności. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
z reguły występujący w danych, zatem określimy to zadanie nieco kolokwialnie - „od tyłu”. Zresztą podano długość przedziału ufności. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Na podstawie wielokrotnych obserwacji ustalono, że rozkład wieku osób pracowników umysłowych w przemyśle ciężkim jest rozkładem normalnym.”
Podano założenie normalności rozkładu wieku pracowników i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Nie mamy informacji na temat tego rozkładu, zatem możemy tylko zapisać 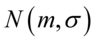 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 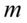 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym 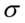 .
.
„W celu oszacowania nieznanej wartości średniej w tym rozkładzie wylosowano niezależnie 17-elementową próbę pracowników.”
W tym momencie dowiadujemy się, że wybrano 17 pracowników, a więc podano liczebność próby: 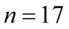 .
.
„Średni wiek w tej próbie wynosił 40 lat, a odchylenie standardowe stanowiło 0,5 czasu średniego.”
Podano średnią dla próby, czyli 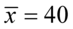 i odchylenie standardowe dla próby. Co prawda nie jest podane bezpośrednio, ale jako połowa średniej, a więc
i odchylenie standardowe dla próby. Co prawda nie jest podane bezpośrednio, ale jako połowa średniej, a więc 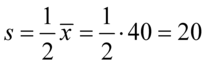 . Oczywiście użyliśmy oznaczeń dla próby.
. Oczywiście użyliśmy oznaczeń dla próby.
„Jaki współczynnik ufności przyjęto przy szacowaniu średniej w rozkładzie wieku ogółu pracowników, jeżeli długość oszacowanego przedziału wynosiła 21,21 lat?”
Naszą niewiadomą jest współczynnik ufności 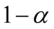 . Określono również długość szacowanego przedziału ufności – 21,21 lat.
. Określono również długość szacowanego przedziału ufności – 21,21 lat.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA ogół pracowników umysłowych w przemyśle ciężkim |
PRÓBA 17 wybranych pracowników |
|
|
|
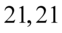 - długość przedziału ufności dla średniej z populacji
- długość przedziału ufności dla średniej z populacji
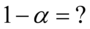 - współczynnik ufności,
- współczynnik ufności, 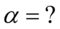
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który został oszacowany przedziałem ufności. Przyjrzyjmy się zdaniu:
„Jaki współczynnik ufności przyjęto przy szacowaniu średniej w rozkładzie wieku ogółu pracowników, jeżeli długość oszacowanego przedziału wynosiła 21,21 lat?”
Wiemy zatem, że zbudowano przedział ufności dla średniej z populacji  - przypominam, że przedział ufności jest budowany dla parametrów z populacji i dlatego nie
- przypominam, że przedział ufności jest budowany dla parametrów z populacji i dlatego nie 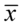 tylko
tylko 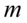 .
.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 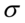 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 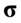 nie jest znana, a liczebność próby
nie jest znana, a liczebność próby 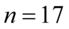 jest mniejsza od 30 (
jest mniejsza od 30 ( 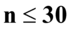 ), zatem wybieramy model II. W danych występuje
), zatem wybieramy model II. W danych występuje 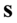 , także interesuje nas pierwsza wersja wzoru z wybranego modelu.
, także interesuje nas pierwsza wersja wzoru z wybranego modelu.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór 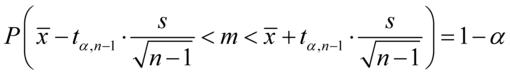 konkretnymi liczbami.
konkretnymi liczbami.
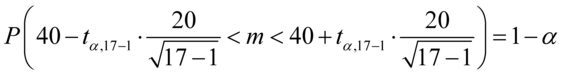
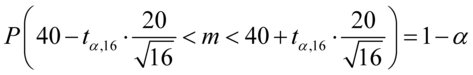
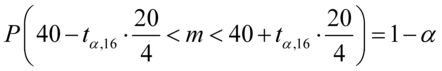
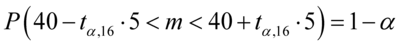
Jak widać, nie możemy uzupełnić współczynnika ufności 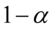 , a tym samym nieznana jest
, a tym samym nieznana jest 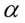 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu t - Studenta (bo w formule znajduje się literka t).
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu t - Studenta (bo w formule znajduje się literka t).
Znamy jednak długość przedziału ufności 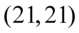 i w związku z tym należy jakoś tą informację wykorzystać.
i w związku z tym należy jakoś tą informację wykorzystać.
Teraz na chwilę zapomnijmy o zadaniu i przypomnijmy sobie w jaki sposób oblicza się jego długość. Weźmy przykładowo przedział 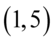 i naszkicujmy go na osi.
i naszkicujmy go na osi.
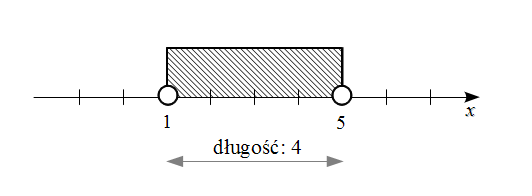
Aby obliczyć długość przedziału należy od końcówki odjąć jego początek, a więc 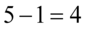 .
.
Podobnie z przedziałem z zadania, a więc 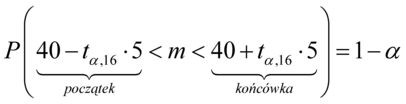 , można oczywiście zapisać go w taki sposób
, można oczywiście zapisać go w taki sposób 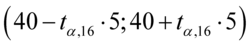 . Co prawda przedział nie jest uzupełniony do końca, ale postępujemy analogicznie:
. Co prawda przedział nie jest uzupełniony do końca, ale postępujemy analogicznie:
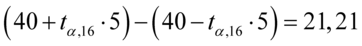
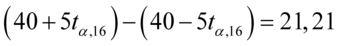
Opuszczamy nawiasy:
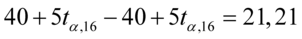
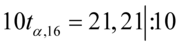
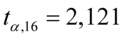
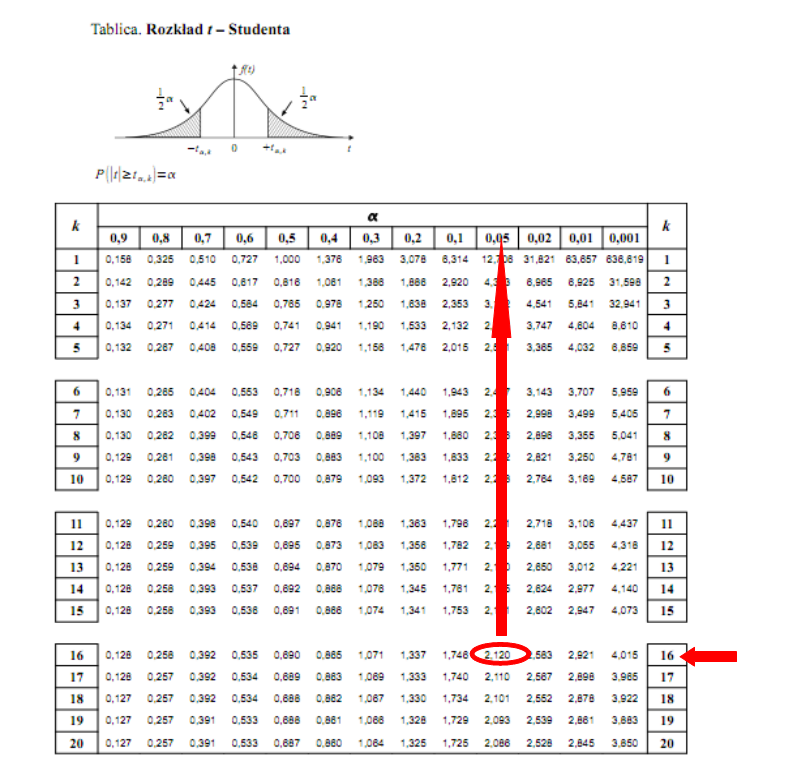
Dopiero teraz wracamy do odczytywania z tablic, jest to tzw. „zadanie od tyłu”, więc i z tablic czytamy od tyłu, a więc szukamy wartości najbliższej 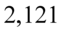 , ale w środku tablicy rozkładu t – Studenta. Zapis
, ale w środku tablicy rozkładu t – Studenta. Zapis 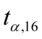 oznacza, że wartości
oznacza, że wartości 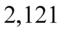 należy poszukiwać w wierszu z 16 stopniami swobody. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle.
należy poszukiwać w wierszu z 16 stopniami swobody. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle.
Najbliższą liczbą 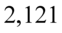 we wnętrzu tablicy przy 16 stopniach swobody stanowi
we wnętrzu tablicy przy 16 stopniach swobody stanowi 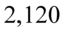 . Wartość
. Wartość 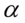 odpowiadająca
odpowiadająca 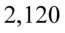 wynosi
wynosi 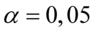 .
.
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy współczynnik ufności: 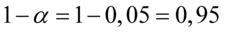 .
.
Interpretacja nie jest konieczna, zresztą i tak nie znamy końcówek przedziału ufności tylko jego długość.
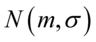 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 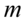 i nieznanym odchyleniu standardowym
i nieznanym odchyleniu standardowym