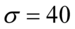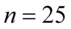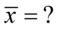Zadanie 16
Średnia frekwencja widzów w kinie na seansie filmowym w jednym z warszawskich kin ma rozkład 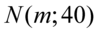 . Na podstawie obserwacji liczby widzów na 25 losowo wybranych seansach kinowych oszacowano przedział liczbowy
. Na podstawie obserwacji liczby widzów na 25 losowo wybranych seansach kinowych oszacowano przedział liczbowy 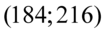 dla nieznanej średniej frekwencji na wszystkich seansach.
dla nieznanej średniej frekwencji na wszystkich seansach.
1. Jaki poziom współczynnika ufności przyjęto przy estymacji ?
2. Ile wynosiła średnia liczba widzów w zbadanej próbie 25 seansów kinowych ?
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Zwracamy uwagę na zdanie:
„Na podstawie obserwacji liczby widzów na 25 losowo wybranych seansach kinowych oszacowano przedział liczbowy 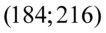 dla nieznanej średniej frekwencji na wszystkich seansach.”
dla nieznanej średniej frekwencji na wszystkich seansach.”
Odnajdujemy w nim słowo: przedział.
„Jaki poziom współczynnika ufności przyjęto przy estymacji ?”
Tu znajduje się słowo: estymacja i współczynnik ufności. Nie ma więc wątpliwości, że zadanie dotyczy estymacji przedziałowej.
W związku z tym, że podane są końcówki przedziału ufności ( 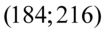 ), a szukane są: współczynnik ufności
), a szukane są: współczynnik ufności  oraz średnia z próby
oraz średnia z próby  z reguły występujące w danych, określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
z reguły występujące w danych, określimy to zadanie nieco kolokwialnie - „od tyłu”. Mimo to, będziemy postępować zgodnie z przyjętym schematem do zadań z estymacji i tylko na pewnym etapie obliczeń wprowadzimy modyfikacje.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Analizujemy zdanie po zdaniu.
„Średnia frekwencja widzów w kinie na seansie filmowym w jednym z warszawskich kin ma rozkład 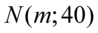 .”
.”
Zapis 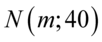 oznacza, że frekwencja widzów w kinie jest zmienną losową o rozkładzie normalnym i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Ponadto możemy odczytać jeden z parametrów rozkładu
oznacza, że frekwencja widzów w kinie jest zmienną losową o rozkładzie normalnym i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Ponadto możemy odczytać jeden z parametrów rozkładu 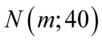 tzn. odchylenie standardowe dla populacji
tzn. odchylenie standardowe dla populacji 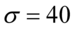 i ostatecznie zapisać jako rozkład normalny o nieznanej średniej
i ostatecznie zapisać jako rozkład normalny o nieznanej średniej 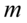 i znanym odchyleniu standardowym
i znanym odchyleniu standardowym 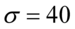 .
.
„Na podstawie obserwacji liczby widzów na 25 losowo wybranych seansach kinowych oszacowano przedział liczbowy 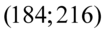 dla nieznanej średniej frekwencji na wszystkich seansach.”
dla nieznanej średniej frekwencji na wszystkich seansach.”
W tym momencie dowiadujemy się, że wybrano 25 widzów, a więc podano liczebność próby: 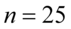 . Podano również końcówki przedziału ufności. Wiemy, że średnia frekwencja na wszystkich seansach zawarta jest w przedziale od 184 do 216.
. Podano również końcówki przedziału ufności. Wiemy, że średnia frekwencja na wszystkich seansach zawarta jest w przedziale od 184 do 216.
„1. Jaki poziom współczynnika ufności przyjęto przy estymacji ?”
Naszą niewiadomą jest współczynnik ufności 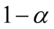 ...
...
„2. Ile wynosiła średnia liczba widzów w zbadanej próbie 25 seansów kinowych ?”
… i nie tylko współczynnik ufności, ponieważ szukamy średniej z próby, a więc stosując odpowiednie oznaczenie 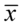 .
.
Podsumowując tworzymy przejrzystą tabelę z danymi:
|
POPULACJA wszystkie seanse kinowe |
PRÓBA 25 wybranych seansów |
|
|
|
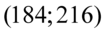 - końcówki przedziału ufności dla średniej z populacji
- końcówki przedziału ufności dla średniej z populacji
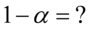 - współczynnik ufności,
- współczynnik ufności, 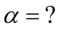
3. WYBÓR ODPOWIEDNIEGO WZORU.
Szukamy parametru, który oszacowano przedziałem ufności i wyłapujemy słowo:
„Na podstawie obserwacji liczby widzów na 25 losowo wybranych seansach kinowych oszacowano przedział liczbowy 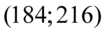 dla nieznanej średniej frekwencji na wszystkich seansach.”
dla nieznanej średniej frekwencji na wszystkich seansach.”
Wyrażenie średniej oznacza, że budowano przedział ufności dla wartości średniej 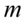 z populacji.
z populacji.
Spójrzmy w kartę wzorów. Dla średniej mamy do wyboru trzy modele wzorów. Teraz wracamy do danych i sprawdzamy, czy 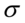 jest znana i jaka jest liczebność próby.
jest znana i jaka jest liczebność próby. 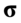 jest znana
jest znana  i tylko model I jest odpowiedni. Liczebność próby nie jest w ogóle istotna.
i tylko model I jest odpowiedni. Liczebność próby nie jest w ogóle istotna.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Wracamy do danych w tabeli i uzupełniamy wzór  konkretnymi liczbami.
konkretnymi liczbami.
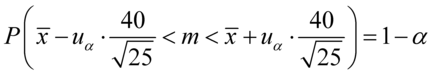
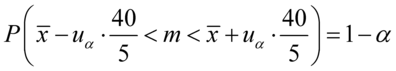
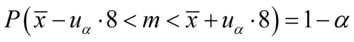
Jak widać, nie możemy uzupełnić współczynnika ufności  , a tym samym nieznana jest
, a tym samym nieznana jest 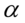 , więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Podobnie średnia
, więc na tym etapie nie mamy możliwości odczytania odpowiedniej statystyki z tablic rozkładu normalnego (bo w formule znajduje się literka u). Podobnie średnia 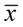 z próby nie jest znana. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
z próby nie jest znana. Znamy jednak końcówki przedziału ufności i w związku z tym możemy je pomocniczo nanieść do wzoru.
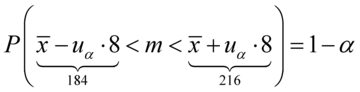
Nie znamy wartości 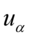 oraz
oraz 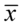 , więc potraktujmy je jako niewiadome i rozwiążmy układ równań aby je wyznaczyć. Zwykła matematyczna zasada – mając dwie niewiadome potrzebujemy z reguły dwóch równań. Pierwsze równanie dotyczy 184, a drugie 216. Zapisujemy zatem:
, więc potraktujmy je jako niewiadome i rozwiążmy układ równań aby je wyznaczyć. Zwykła matematyczna zasada – mając dwie niewiadome potrzebujemy z reguły dwóch równań. Pierwsze równanie dotyczy 184, a drugie 216. Zapisujemy zatem:
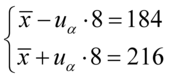

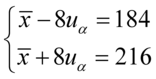
Sposób rozwiązania układu jest dowolny, chociaż tu najwygodniej zastosować metodę przeciwnych współczynników. Dodajemy stronami obydwa równania:
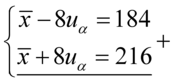
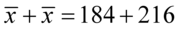
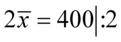
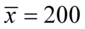
Wracamy do układu i wybierając dowolne równanie wyliczamy  , średnią
, średnią 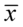 mamy z głowy:
mamy z głowy:
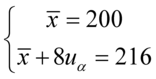

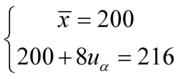

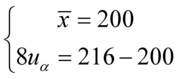

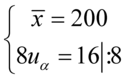

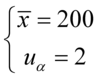
Jeśli komuś z Was jest wygodniej rozwiązywać układy równań z literką 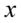 i
i 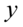 , to możecie spokojnie na początku zastąpić symbole np.
, to możecie spokojnie na początku zastąpić symbole np. 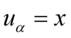 i
i  lub odwrotnie.
lub odwrotnie.
Dopiero teraz wracamy do odczytywania z tablic, jest to tzw. „zadanie od tyłu”, więc i z tablic czytamy od tyłu, a więc szukamy wartości najbliższej 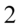 , ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle.
, ale w środku tablicy rozkładu normalnego. Wynikiem odczytywania są obrzeża tablicy, a więc inaczej niż zwykle.
Najbliższą wartością  we wnętrzu tablicy rozkładu normalnego stanowi
we wnętrzu tablicy rozkładu normalnego stanowi 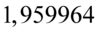 (jeśli dysponujecie dokładniejszymi tablicami, to wynik będzie nieco inny). Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy
(jeśli dysponujecie dokładniejszymi tablicami, to wynik będzie nieco inny). Odczytując sumuje się wartości znajdujące się na obrzeżach tzn. z kolumny, która stanowi części dziesiętne i z wiersza, który traktujemy jako części setne. Sumujemy 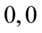 i
i 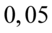 czyli
czyli 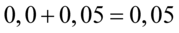 . Pamiętajmy, że jest to
. Pamiętajmy, że jest to 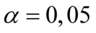 .
.
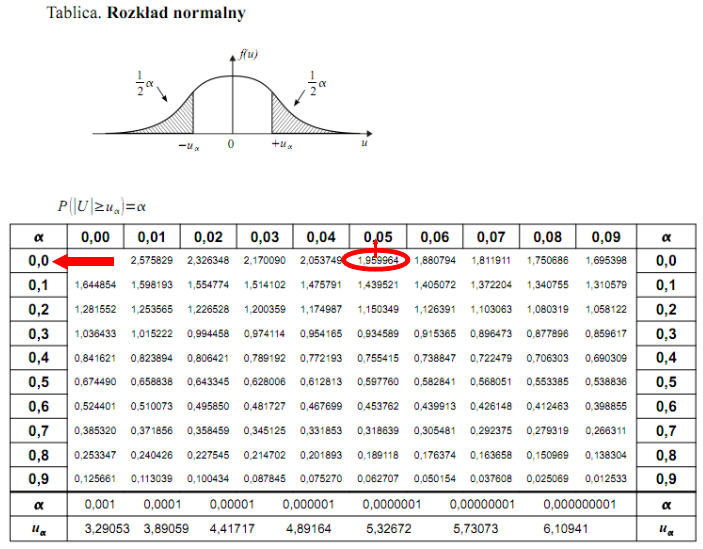
5. WYNIK I INTERPRETACJA.
Ostatecznie otrzymujemy współczynnik ufności 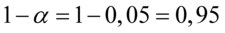 i średnią z próby
i średnią z próby 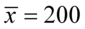 .
.
Interpretacja nie jest tu raczej niezbędna, ale brzmi następująco:
Z ufnością 0,95 nieznana średnia frekwencja na wszystkich seansach mieści się w przedziale od 184 do 216.
Zadanie pochodzi z: Statystyka zbiór zadań / Helena Kassyk-Rokicka. - Polskie Wydawnictwo Ekonomiczne - ISBN 83-208-1107-4
 - rozkład normalny o nieznanej średniej
- rozkład normalny o nieznanej średniej 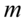 i znanym odchyleniu standardowym
i znanym odchyleniu standardowym