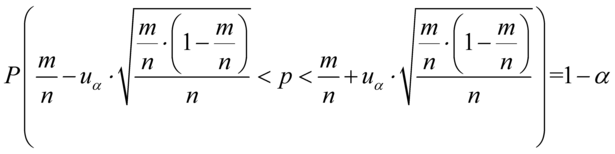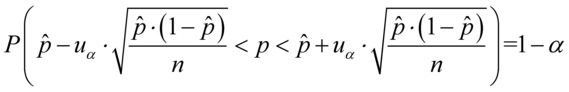Estymacja przedziałowa
Na początek trochę teorii. Czym jest estymacja przedziałowa?
Estymacja przedziałowa jest metodą służącą do szacowania parametrów rozkładu zmiennej losowej w populacji generalnej. Definicja nie jest zbyt zachęcająca, więc wyjaśnię to inaczej. Estymacja przedziałowa pozwala nam oszacować z pewnym prawdopodobieństwem wartość różnych parametrów dla całej populacji np. średniej 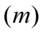 , wariancji
, wariancji 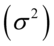 , odchylenia standardowego
, odchylenia standardowego 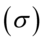 , wskaźnika struktury
, wskaźnika struktury 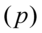 (procentu, częstości, frakcji, odsetka) na podstawie wybranej próbki. W estymacji przedziałowej wynikiem oceny parametru nie jest konkretna wartość, ale przedział, w którym z określonym prawdopodobieństwem mieści się szacowana wartość parametru.
(procentu, częstości, frakcji, odsetka) na podstawie wybranej próbki. W estymacji przedziałowej wynikiem oceny parametru nie jest konkretna wartość, ale przedział, w którym z określonym prawdopodobieństwem mieści się szacowana wartość parametru.
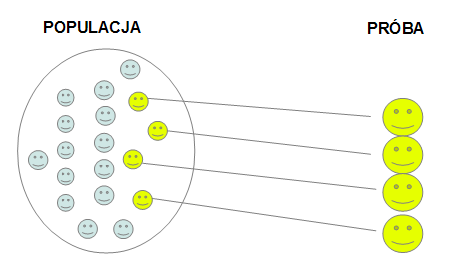
Wyjaśnijmy różnicę między próbą a populacją. Populacją jest cała zbiorowość, a próba jest wybraną częścią populacji. Posłużmy się konkretnymi przykładami:
- populacją jest ludność zamieszkująca Polskę, a próbą z tej populacji jest ludność wybranego województwa,
- populację stanowią drzewa na danym obszarze, a próbą z tej populacji jest np. 30 wybranych drzew, itd.
Graficznie:
Po wybraniu elementów próby możemy wyliczyć dla niej podstawowe parametry, tzn. średnią 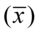 , wariancję
, wariancję 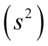 lub
lub 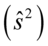 oraz odchylenie standardowe
oraz odchylenie standardowe 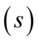 lub
lub 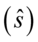 , czyli zbadać ją wszerz i wzdłuż. Kolejnym etapem jest przełożenie wyników z próby na populację i właśnie w tym momencie pojawia się estymacja przedziałowa. Upraszczając badamy próbkę i na jej podstawie staramy się coś powiedzieć o całej populacji. Z reguły populacja jest zbyt duża, aby móc przenieść wnioski ze 100% pewnością poprawności wyników, dlatego robimy to z pewnym prawdopodobieństwem. Najczęściej jest to 0,99 , 0,98 , 0,95 , 0,9. W zadaniach prawdopodobieństwo określane jest jako współczynnik ufności i zapisywane jako
, czyli zbadać ją wszerz i wzdłuż. Kolejnym etapem jest przełożenie wyników z próby na populację i właśnie w tym momencie pojawia się estymacja przedziałowa. Upraszczając badamy próbkę i na jej podstawie staramy się coś powiedzieć o całej populacji. Z reguły populacja jest zbyt duża, aby móc przenieść wnioski ze 100% pewnością poprawności wyników, dlatego robimy to z pewnym prawdopodobieństwem. Najczęściej jest to 0,99 , 0,98 , 0,95 , 0,9. W zadaniach prawdopodobieństwo określane jest jako współczynnik ufności i zapisywane jako 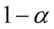 . Im większa wartość tego współczynnika, tym szerszy przedział ufności, a więc mniejsza dokładność oszacowania parametru, ponieważ dłuższy przedział powoduje większy wybór szacowanych wartości. Im mniejsza wartość
. Im większa wartość tego współczynnika, tym szerszy przedział ufności, a więc mniejsza dokładność oszacowania parametru, ponieważ dłuższy przedział powoduje większy wybór szacowanych wartości. Im mniejsza wartość 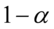 , tym większa dokładność estymacji, ale automatycznie oznacza to większe prawdopodobieństwo popełnienia błędu przy szacowaniu.
, tym większa dokładność estymacji, ale automatycznie oznacza to większe prawdopodobieństwo popełnienia błędu przy szacowaniu.
Teraz przedstawię swój tok myślenia przy rozwiązywaniu zadań dotyczących estymacji przedziałowej, który można uznać za schemat przy tego typu zadaniach.
1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?
Proponuje przeczytać całe zadanie i zwrócić uwagę na tzw. słowa – klucze:
- oszacować przedziałowo ...
- zbudować przedział ufności pokrywający ...
- wskazać przedział, w którym mieści się ...
Praktycznie zawsze występuje wyrażenie współczynnik ufności 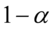 .
.
Jeżeli znaleźliśmy jakikolwiek z tych zwrotów na pewno mamy do czynienia z zadaniem dotyczącym estymacji przedziałowej.
2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.
Bardzo ważne jest prawidłowe wypisanie danych, ponieważ jeśli na tym etapie wkradnie się pomyłka, to zadanie nie będzie poprawnie rozwiązane.
Wspominałam wcześniej o różnicy między populacją a próbą i tu właśnie istotne jest wyłapanie danych dotyczących próby i populacji. Próba i populacja charakteryzują się konkretnymi parametrami, tzn. średnią, wariancją, odchyleniem standardowym, a ich oznaczenia różnią się. Oto tabela ukazująca różnice w oznaczeniach.
|
POPULACJA |
PRÓBA |
|
|
|
|
Jeżeli w zadaniu jest wspomniane, że cecha ma rozkład normalny, to zawsze dotyczy populacji, ponieważ próba z reguły jest za mała, aby to stwierdzić. Zapisujemy jako: |
|
Z reguły podaje się współczynnik ufności 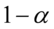 , który wyrażony jest w ułamku lub w procentach. Zamieniajmy procenty na ułamki i od razu wyznaczajmy samą
, który wyrażony jest w ułamku lub w procentach. Zamieniajmy procenty na ułamki i od razu wyznaczajmy samą 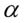 , ponieważ będzie ona nam potrzebna do czytania z tablic.
, ponieważ będzie ona nam potrzebna do czytania z tablic.
Teraz kilka uwag odnośnie 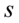 i
i 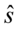 oraz
oraz 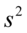 i
i 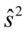 . Oznaczenia z tzw. daszkiem to odpowiednio odchylenie i wariancja nieobciążona. W praktyce różnią się od siebie sposobem liczenia, tzn.
. Oznaczenia z tzw. daszkiem to odpowiednio odchylenie i wariancja nieobciążona. W praktyce różnią się od siebie sposobem liczenia, tzn. 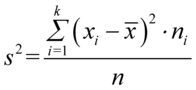 a
a 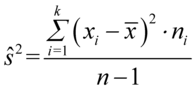 (w
(w 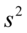 dzielimy przez
dzielimy przez 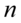 , a w
, a w 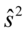 dzielimy przez
dzielimy przez 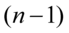 ). Jeśli w zadaniu będzie powiedziane, że odchylenie standardowe lub wariancja z próby wynoszą np. 7, to odpowiednio stosujemy zapis
). Jeśli w zadaniu będzie powiedziane, że odchylenie standardowe lub wariancja z próby wynoszą np. 7, to odpowiednio stosujemy zapis 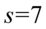 (
( 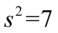 ). Używamy zapisu z daszkiem tylko w przypadku, gdy znajdziemy słowo nieobciążona lub po prostu w zadaniu jest wyraźny zapis
). Używamy zapisu z daszkiem tylko w przypadku, gdy znajdziemy słowo nieobciążona lub po prostu w zadaniu jest wyraźny zapis 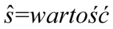 .
.
W przypadku wyliczania wariancji ze wzorów 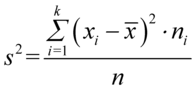 lub
lub 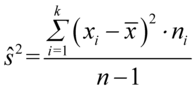 , to będziemy z nich korzystać tylko wtedy, gdy w zadaniu nie podano „na tacy”, że odchylenie czy wariancja ma konkretną wartość. Najczęściej podana jest tabela z wynikami z próby lub po prostu wyniki podane po przecinku i tu na własną rękę trzeba wyliczać średnią, wariancję czy odchylenie standardowe (jest to zagadnienie ze statystyki opisowej). Korzystamy najczęściej ze wzorów w wersji bez daszka. Tak więc tu pojawia się informacja godna zapamiętania – jeśli dysponujemy tabelką lub wynikami z próby zawsze możemy policzyć średnią, wariancję, odchylenie standardowe.
, to będziemy z nich korzystać tylko wtedy, gdy w zadaniu nie podano „na tacy”, że odchylenie czy wariancja ma konkretną wartość. Najczęściej podana jest tabela z wynikami z próby lub po prostu wyniki podane po przecinku i tu na własną rękę trzeba wyliczać średnią, wariancję czy odchylenie standardowe (jest to zagadnienie ze statystyki opisowej). Korzystamy najczęściej ze wzorów w wersji bez daszka. Tak więc tu pojawia się informacja godna zapamiętania – jeśli dysponujemy tabelką lub wynikami z próby zawsze możemy policzyć średnią, wariancję, odchylenie standardowe.
Czasem bywa, że musimy podać 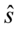 lub
lub 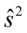 dysponując
dysponując 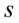 albo
albo 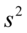 .
.
Oto wzory: 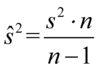 , a
, a 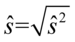 .
.
W jaki sposób wypisując dane odróżniamy próbę od populacji? Najlepiej czytajmy po jednym zdaniu. Jeżeli pojawiają się zwroty np. wylosowano próbę, zmierzono x obserwacji, obserwowano x próbek, zbadano... to jakiekolwiek dane po tych słowach zapisujemy używając symboli dla próby, zresztą i tak pojawia się się konkretna liczba mówiąca o liczebności wylosowanej próby. Jeśli nie ma wyraźnie niczego na temat próby lub występuje zwrot: rozkład normalny ze średnią bądź odchyleniem standardowym to używamy symboli dla populacji.
Nie należy się dziwić, gdy po wypisaniu danych okaże się, że miejsce na parametry z populacji jest puste. To dość częsta sytuacja.
3. WYBÓR ODPOWIEDNIEGO WZORU.
Po wypisaniu danych należy wybrać odpowiedni wzór. W tym celu szukamy w zadaniu dla jakiego parametru mamy zbudować przedział ufności tzn. średniej (wartości oczekiwanej), wariancji, odchylenia standardowego czy wskaźnika struktury (częstości, frakcji, odsetka, procentu). Pamiętajmy, że szacujemy parametry z populacji, a więc używamy oznaczeń 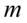 ,
, 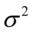 ,
, 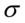 ,
, 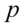 ( w końcu po to badamy próbę, by móc coś powiedzieć na temat całej zbiorowości).
( w końcu po to badamy próbę, by móc coś powiedzieć na temat całej zbiorowości).
W przypadku, gdy mamy do czynienia z zadaniem, gdzie podany jest przedział ufności, ale szukamy np. współczynnika ufności albo innych zmiennych, które przeważnie są danymi (zadanie „od tyłu” :D) również stosujemy ten mechanizm.
Kartę ze wzorami można pobrać tu.
W tabeli poniżej przedstawione zostaną charakterystyczne sformułowania i dopasowanie do odpowiednich wzorów:
|
Przykładowe wyrażenia |
Szacowany parametr |
Wzór lub wzory do wyboru |
|
- przedział ufności pokrywający średni..., - wskaż przedział, w którym znajdzie się przeciętny...,
*jeśli w zadaniu nie ma wyróżnionego parametru, który mamy oszacować przedziałem ufności, a w danych wypisano
|
średnia (wartość oczekiwana) - |
MODEL I Populacja generalna ma rozkład normalny MODEL II Populacja generalna ma rozkład normalny lub MODEL III Populacja generalna na rozkład normalny |
|
- przedział szacujący wariancję, - przedział ufności pokrywający nieznaną wartość wariancji,
* jeśli nie określono dla jakiego parametru należy zbudować przedział ufności, a w zadaniu występuje słowo: zróżnicowanie, to przyjmujemy wariancję |
wariancja - |
Populacja generalna ma rozkład normalny lub |
|
- przedział dla odchylenia standardowego
* jeśli nie określono dla jakiego parametru należy zbudować przedział ufności, a w zadaniu występuje słowo: zróżnicowanie, to przyjmujemy wariancję |
odchylenie standardowe - |
MODEL I Populacja generalna ma rozkład normalny
lub MODEL II Populacja generalna ma rozkład normalny gdzie: |
|
- wskaż przedział ufności dla nieznanej częstości, - przedział ufności dla odsetka, - przedział, w którym zawarty jest procent...., - oszacować metodą przedziału ufności frakcję, - wyznaczyć przedział ufności pokrywający nieznany wskaźnik struktury, - przedział ufności dla udziału, - oszacować metodą przedziału ufności współczynnik.
*jeśli w zadaniu nie ma wyróżnionego parametru, który mamy oszacować przedziałem ufności, a w danych wypisano |
wskaźnik struktury - |
lub |
Jeśli już wiemy jaki parametr mamy oszacować przedziałem ufności, to wybieramy wzór na podstawie danych, które wypisaliśmy wcześniej. Z tabeli wynika, że średnia i wariancja mają kilka modeli wzorów do wyboru. Tu kierujemy się elementami wyszczególnionymi kolorem czerwonym tzn. liczebnością próby i czy 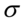 jest znana.
jest znana.
4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.
Po wybraniu odpowiedniego wzoru należy uzupełnić go wielkościami wypisanymi w danych. Dla przykładu użyję dowolnego wzoru:

Wielkości zaznaczone na zielono zastępujemy liczbami z danych, reszta zostaje nienaruszona.
We wzorach pojawiają się różne litery, które wcześniej nie były wypisane w danych tzn. 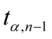 ,
, 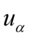 ,
, 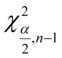 ,
, 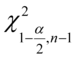 . Symbole te po uzupełnieniu
. Symbole te po uzupełnieniu  i
i 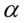 oznaczają konieczność odczytania wartości statystyk z tablic:
oznaczają konieczność odczytania wartości statystyk z tablic:
-
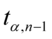 - tablice t – Studenta
- tablice t – Studenta -
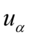 - tablice rozkładu normalnego (nie mylić z tablicami dystrybuanty rozkładu normalnego)
- tablice rozkładu normalnego (nie mylić z tablicami dystrybuanty rozkładu normalnego) -
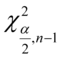 ,
, 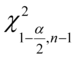 - tablice chi - kwadrat
- tablice chi - kwadrat
Odpowiednie tablice można pobrać tu.
Odczytywanie statystyk z tablic jest jest bardzo prostą czynnością i będzie przedstawiona na konkretnych przykładach. Po odczytaniu cały symbol tzn. 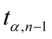 ,
, 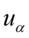 ,
, 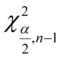 ,
, 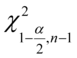 zastępujemy jedną liczbą.
zastępujemy jedną liczbą.
Podsumowując ten wątek można dojść do wniosku, że dopiero po wybraniu wzoru należy odczytać wartości statystyk z odpowiednich tablic. Tak więc wzór spokojnie nam wskaże, które tablice mamy wybrać :).
5. WYNIK I INTERPRETACJA.
Rezultatem obliczeń jest zapis:
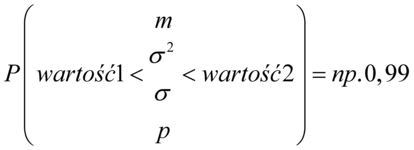 , gdzie oczywiście symbole
, gdzie oczywiście symbole 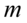 ,
, 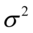 ,
, 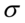 ,
, 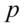 wybierane są opcjonalnie w zależności od treści zadania. Oczywiście nie dotyczy to zadań „od tyłu”, gdzie szukamy współczynnika ufności lub innych wartości, które najczęściej są wypisywane w danych.
wybierane są opcjonalnie w zależności od treści zadania. Oczywiście nie dotyczy to zadań „od tyłu”, gdzie szukamy współczynnika ufności lub innych wartości, które najczęściej są wypisywane w danych.
Jeśli wymagana jest interpretacja, to wygląda ona zawsze bardzo podobnie:
Z ufnością  (tu wpisujemy wartość współczynnika ufności
(tu wpisujemy wartość współczynnika ufności 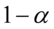 ) wartość nieznanej(-ego)
) wartość nieznanej(-ego)  (średniej, wariancji, odchylenia standardowego, wskaźnika struktury) dla całej populacji
(średniej, wariancji, odchylenia standardowego, wskaźnika struktury) dla całej populacji  (czegoś tam :) zależy o czym mowa w zadaniu) mieści się w przedziale od
(czegoś tam :) zależy o czym mowa w zadaniu) mieści się w przedziale od 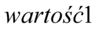 do
do 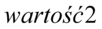 .
.
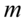 - średnia
- średnia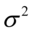 - wariancja
- wariancja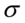 -odchylenie standardowe
-odchylenie standardowe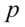 - wskaźnik struktury, odsetek, procent, częstość, frakcja
- wskaźnik struktury, odsetek, procent, częstość, frakcja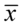 - średnia
- średnia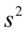 ,
, 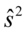 - wariancja
- wariancja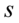 ,
, 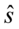 - odchylenie standardowe
- odchylenie standardowe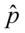 -wskaźnik struktury, odsetek, procent, częstość, frakcja, udział, współczynnik
-wskaźnik struktury, odsetek, procent, częstość, frakcja, udział, współczynnik 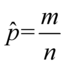
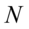 – liczebność populacji
– liczebność populacji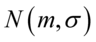 , a czytamy: rozkład normalny o średniej
, a czytamy: rozkład normalny o średniej 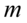 i odchyleniu standardowym
i odchyleniu standardowym 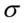
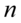 – liczebność próby
– liczebność próby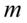 - ilość obserwacji spośród próby np. wylosowaliśmy
- ilość obserwacji spośród próby np. wylosowaliśmy 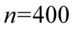 osób i
osób i 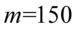 spośród nich kupuje mleko firmy X. Jak widać oznaczenie pokrywa się ze średnią z populacji, ale te dwie wielkości w zadaniach nigdy nie występują jednocześnie.
spośród nich kupuje mleko firmy X. Jak widać oznaczenie pokrywa się ze średnią z populacji, ale te dwie wielkości w zadaniach nigdy nie występują jednocześnie.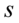 lub
lub 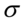 , to przyjmujemy, że szacujemy wartość średnią
, to przyjmujemy, że szacujemy wartość średnią 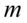
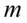
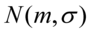 , gdzie:
, gdzie:  - znane.
- znane.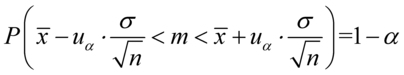
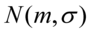 , gdzie:
, gdzie:  - nieznane,
- nieznane, 
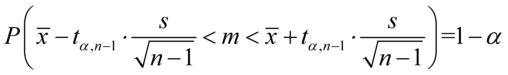 , gdy dane jest
, gdy dane jest 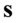
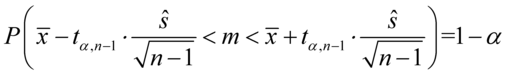 , gdy dane jest
, gdy dane jest 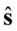
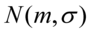 bądź inny rozkład, gdzie:
bądź inny rozkład, gdzie:  - nieznane,
- nieznane, 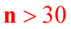
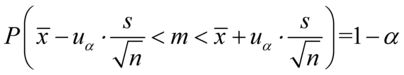
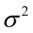 lub odchylenie standardowe
lub odchylenie standardowe 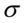
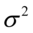
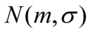 , gdzie:
, gdzie:  - nieznane,
- nieznane, 
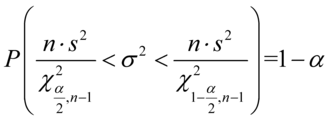 , gdy dane jest
, gdy dane jest 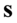
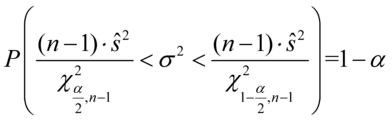 , gdy dane jest
, gdy dane jest 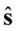
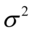 lub odchylenie standardowe
lub odchylenie standardowe 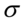
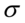
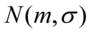 , gdzie:
, gdzie:  - nieznane,
- nieznane, 
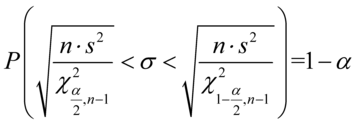 , gdy dane jest
, gdy dane jest 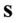
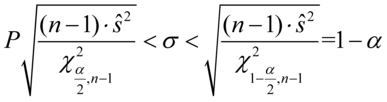 , gdy dane jest
, gdy dane jest 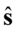
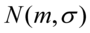 lub zbliżony do normalnego,
lub zbliżony do normalnego, - nieznane,
- nieznane, 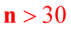
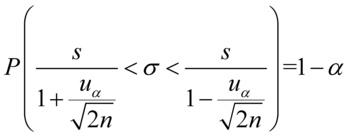
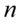 oraz
oraz 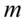 (
( 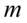 - ilość obserwacji spośród próby), to przyjmujemy, że szacujemy wskaźnik struktury
- ilość obserwacji spośród próby), to przyjmujemy, że szacujemy wskaźnik struktury 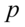
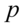 (używane zamiennie: frakcja, procent, odsetek, częstość)
(używane zamiennie: frakcja, procent, odsetek, częstość)