Cecha X ma rozkład 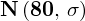. Wyznaczyć przedział ufności dla odchylenia standardowego, na poziomie ufności 0,98, jeśli na podstawie 10-elementowej próby otrzymano wariancję z próby równą 18.

1. JAK ROZPOZNAĆ ZADANIE DOTYCZĄCE ESTYMACJI PRZEDZIAŁOWEJ ?

Po przeczytaniu całego zadania zwracamy uwagę na zdanie:

Wyznaczyć przedział ufności dla odchylenia standardowego, na poziomie ufności 0,98, jeśli na podstawie 10-elementowej próby otrzymano wariancję z próby równą 18.

Występują tu zwroty: wyznaczyć przedział ufności i poziom ufności - w związku z tym na pewno jest to zadanie dotyczące estymacji przedziałowej.

2. ANALIZA I PRAWIDŁOWE WYPISANIE DANYCH.

Analizujemy zdanie po zdaniu.

Cecha X ma rozkład .

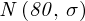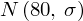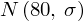Zapis oznacza, że cecha X charakteryzuje się rozkładem normalnym i to już odnosi się do populacji (wcześniej wspominałam w części teoretycznej, że próba jest z reguły za mała aby stwierdzić rozkład normalny). Symbol odczytujemy jako rozkład normalny o znanej średniej i nieznanym odchyleniu standardowym .

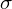Wyznaczyć przedział ufności dla odchylenia standardowego, na poziomie ufności 0,98, jeśli na podstawie 10-elementowej próby otrzymano wariancję z próby równą 18.

Podano współczynnik ufności 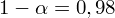. Od razu wyznaczamy 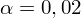. W tym zdaniu zaczyna się również opis próby, ponieważ pojawia się informacja na temat wylosowania konkretnej ilości elementów. Oznaczamy więc liczebność próby 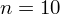. Dodatkowo podano jeden z podstawowych parametrów dla próby na podstawie przeprowadzonego badania, a mianowicie wariancję 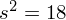(oczywiście użyto oznaczenia dla próby). Można od razu wyznaczyć odchylenie standardowe jako pierwiastek kwadratowy z wariancji .

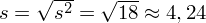Podsumowując tworzymy przejrzystą tabelę z danymi:

POPULACJA nieokreślona	PRÓBA 10 wybranych elementów
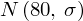- rozkład normalny o znanej średniej i nieznanym odchyleniu standardowym

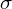
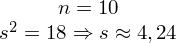
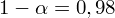- współczynnik ufności,

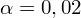
3. WYBÓR ODPOWIEDNIEGO WZORU.

Szukamy parametru, który należy oszacować przedziałem ufności i w ostatnim zdaniu wyłapujemy słowo:

Wyznaczyć przedział ufności dla odchylenia standardowego , na poziomie ufności 0,98, jeśli na podstawie 10-elementowej próby otrzymano wariancję z próby równą 18.

Zwrot odchylenie standardowe oznacza, że będziemy budować przedział ufności oczywiście dla odchylenia standardowego 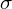z populacji.

Spójrzmy w kartę wzorów. Dla odchylenia standardowego mamy do wyboru dwa modele. Teraz wracamy do danych i sprawdzamy, czy jest 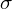znana i jaka jest liczebn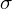ość próby. nie jest znana , a liczebność próby 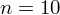jest mniejsza od 30 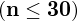, zatem wybieramy model I . W danych występuje , także interesuje nas pierwsza wersja wzoru z wybranego modelu.

4. UZUPEŁNIANIE WYBRANEGO WZORU I OBLICZENIA.

Wracamy do danych z tabeli i uzupełniamy wzór 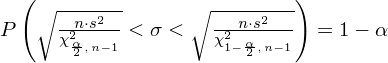konkretnymi danymi.

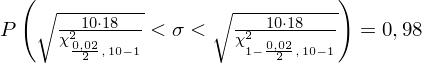
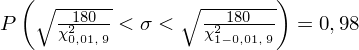
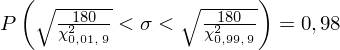
Teraz należy odczytać odpowiednią statystykę z tablic. W formule znajduje się literka 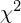(grecka litera czyt. chi ), zatem skorzystamy z tablic rozkładu chi-kwadrat (link). W tym przypadku będziemy odczytywać statystykę dwukrotnie, ponieważ w uzupełnionym wzorze występują dwa nieco różniące się symbole: 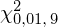oraz 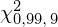. Zapis 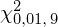oznacza konieczność odnalezienia w tablicach statystyki dla 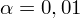i 9 stopni swobody:

Z kolei zapis 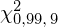oznacza konieczność odnalezienia w tablicach statystyki dla 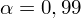i 9 stopni swobody:

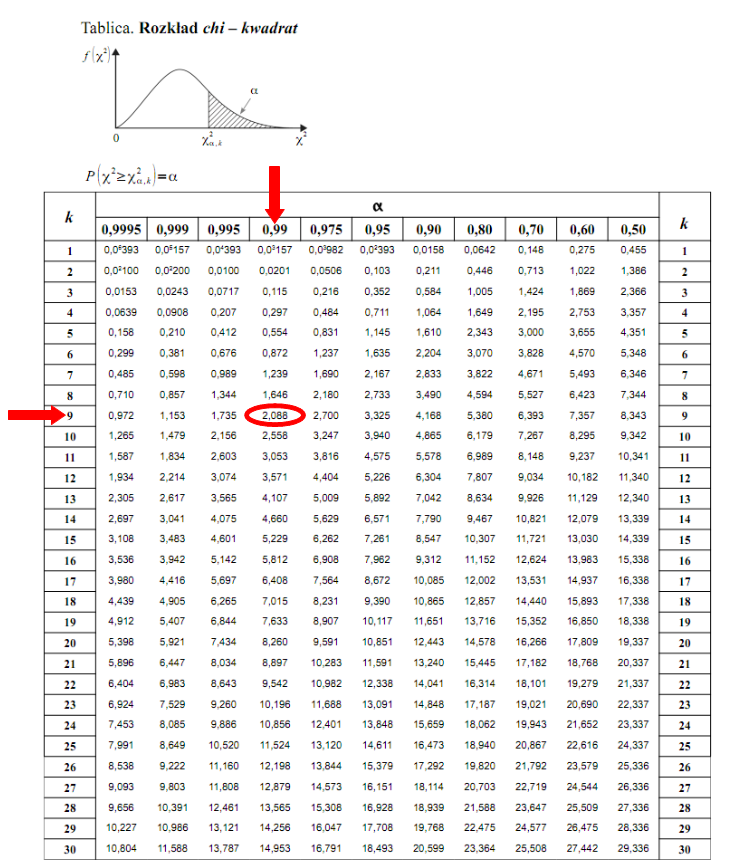
Wracamy do obliczeń i podstawiamy 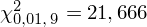oraz :

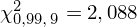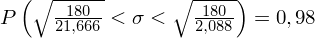
5. WYNIK I INTERPRETACJA.

Ostatecznie otrzymujemy:

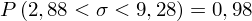
Interpretacja brzmi następująco: Z ufnością 0,98 nieznane odchylenie standardowe cechy X mieści się w przedziale od 2,88 do 9,28.

Statystyka elementy teorii i zadania / Stanisława Ostasiewicz, Zofia Rusnak, Urszula Siedlecka, Wrocław : Wydawnictwo Akademii Ekonomicznej im. Oskara Langego, 2006. - Wyd. 6 popr., ISBN: 83-7011-783-X, str. 280