
Na wstępie uprzedzam, aby w miarę dobrze opanować liczenie całek, zwłaszcza przy użyciu metody przez podstawienie i przez części, trzeba mieć jakiekolwiek pojęcie o wyznaczaniu pochodnych !!!
Wyznaczanie całki nieoznaczonej dla funkcji 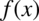 tzn. wyznaczanie funkcji pierwotnej
tzn. wyznaczanie funkcji pierwotnej 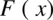 nazywamy całkowaniem funkcji
nazywamy całkowaniem funkcji 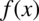 .
.
Zbiór wszystkich funkcji pierwotnych funkcji 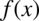 nazywamy całką nieoznaczoną funkcji
nazywamy całką nieoznaczoną funkcji 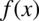 i oznaczamy ją symbolem:
i oznaczamy ją symbolem:
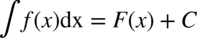
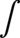 - symbol całki
- symbol całki
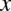 – zmienna całkowania
– zmienna całkowania
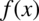 – funkcja podcałkowa
– funkcja podcałkowa
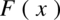 – funkcja pierwotna, całka nieoznaczona
– funkcja pierwotna, całka nieoznaczona 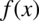
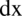 – symbol oznaczający zmienną po której całkujemy, tzn. zmienną, względem której wyznaczamy funkcję pierwotną jest zmienna
– symbol oznaczający zmienną po której całkujemy, tzn. zmienną, względem której wyznaczamy funkcję pierwotną jest zmienna 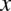 , występuje zawsze razem ze znakiem całki
, występuje zawsze razem ze znakiem całki 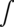 , gdy symbol całki znika, to również
, gdy symbol całki znika, to również 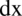 znika
znika
 – stała nazywana zmienną całkowania (dowolna liczba rzeczywista -
– stała nazywana zmienną całkowania (dowolna liczba rzeczywista - 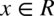 ), pojawia się w wyniku, nigdy nie występuje jednocześnie z symbolem całki
), pojawia się w wyniku, nigdy nie występuje jednocześnie z symbolem całki
Jeżeli 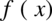 jest ciągła w danym przedziale to jest w tym przedziale również całkowalna.
jest ciągła w danym przedziale to jest w tym przedziale również całkowalna.
Całkowanie to działanie odwrotne w stosunku do różniczkowania czyli wyznaczania pochodnej funkcji (analogicznie jak dodawanie i odejmowanie, potęgowanie i pierwiastkowanie). Inaczej mówiąc jeżeli z już wyliczonej całki policzymy pochodną to mamy otrzymać funkcję, z której liczyliśmy całkę – można tak robić w ramach sprawdzenia wyniku.
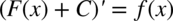
Całkowanie jako działanie odwrotne do różniczkowania nie jest działaniem jednoznacznym, ponieważ funkcja pierwotna nie jest jednoznacznie wyznaczona, bo występuje w niej stała  , która może być dowolną liczbą. Na przykład całka z funkcji
, która może być dowolną liczbą. Na przykład całka z funkcji 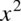 wynosi
wynosi 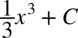 , gdzie
, gdzie  może być
może być 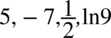 , albo każdą inną liczbą. Kiedy policzymy pochodną z wyniku (nie ważne przy jakim
, albo każdą inną liczbą. Kiedy policzymy pochodną z wyniku (nie ważne przy jakim  ) otrzymamy znów
) otrzymamy znów 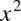 (
( 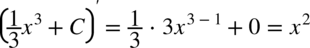 dla przypomnienia pochodna ze stałej wynosi
dla przypomnienia pochodna ze stałej wynosi 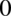 ). Tak więc całkując otrzymujemy całą rodzinę funkcji pierwotnych z różnorodnymi współczynnikami
). Tak więc całkując otrzymujemy całą rodzinę funkcji pierwotnych z różnorodnymi współczynnikami  , podczas gdy funkcja podcałkowa jest tylko jedna i na tym polega właśnie niejednoznaczność.
, podczas gdy funkcja podcałkowa jest tylko jedna i na tym polega właśnie niejednoznaczność.
Jeżeli funkcja jest całkowalna na pewnym przedziale, gdzie 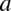 jest dowolną liczbą, ale różną od zera to korzystamy ze wzoru:
jest dowolną liczbą, ale różną od zera to korzystamy ze wzoru:
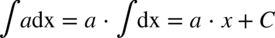
Oznacza to, że stały czynnik występujący w funkcji podcałkowej można wyłączyć przed znak całki. Mówiąc jeszcze prościej, jeżeli w funkcji podcałkowej nie ma zmiennej 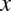 (oczywiście jeżeli całkujemy po
(oczywiście jeżeli całkujemy po 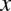 ), to wyciągamy czynnik przed znak całki, ponieważ każde inne symbole poza
), to wyciągamy czynnik przed znak całki, ponieważ każde inne symbole poza 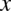 to stałe. Oto przykłady:
to stałe. Oto przykłady:
CAŁKA 1
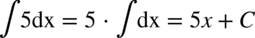
CAŁKA 2
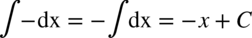 lub
lub 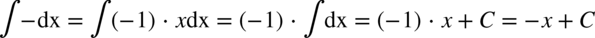
CAŁKA 3
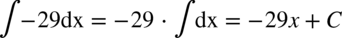
CAŁKA 4
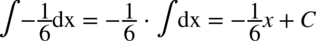
CAŁKA 5
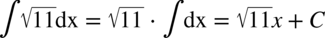
CAŁKA 6
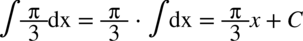
CAŁKA 7
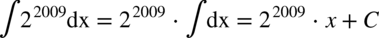
CAŁKA 8
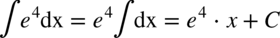 ,
, 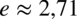
CAŁKA 9
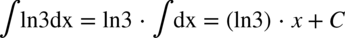
CAŁKA 10
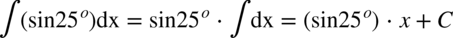
Jeżeli symbol 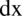 występuje w ułamku, to można go „zrzucić” z funkcji podcałkowej, jeżeli przy
występuje w ułamku, to można go „zrzucić” z funkcji podcałkowej, jeżeli przy 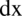 nie było żadnej liczby to znajduje się tam
nie było żadnej liczby to znajduje się tam 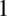 , bo przecież
, bo przecież 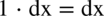 .
.
CAŁKA 11
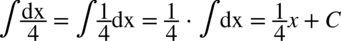
CAŁKA 12
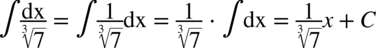
CAŁKA 13
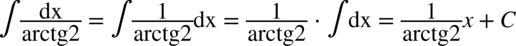
CAŁKA 14
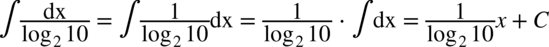
CAŁKA 15
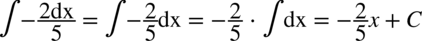
Jeszcze raz dla przypomnienia, każda litera lub inny symbol poza zmienną całkowania, która jest wskazywana przez 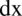 jeżeli jest to
jeżeli jest to 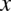 ,
, 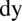 jeżeli jest to
jeżeli jest to 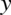 ,
, 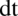 jeżeli jest to
jeżeli jest to  można wyłączyć przed znak całki !
można wyłączyć przed znak całki !
CAŁKA 16
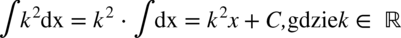
CAŁKA 17
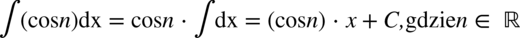
CAŁKA 18
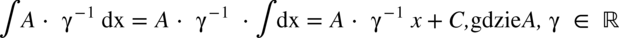
CAŁKA 19
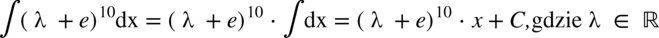
Teraz zajmiemy się podstawowym wzorem na całki:
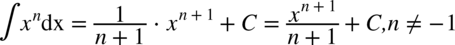
Przykłady:
CAŁKA 20
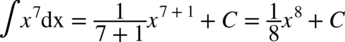
CAŁKA 21
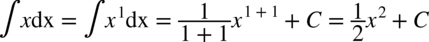
CAŁKA 22
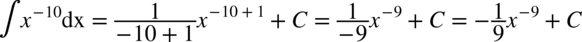
CAŁKA 23
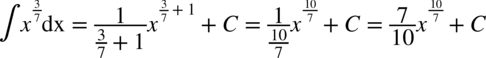
CAŁKA 24
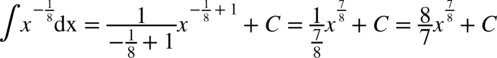
Można też w podany sposób obliczać całki, w których w pojawia się kreska ułamkowa, ale w mianowniku nie ma dodawania ani odejmowania. Korzystamy ze wzoru na potęgi:
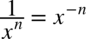
CAŁKA 25
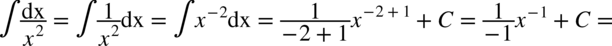
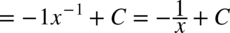
CAŁKA 26
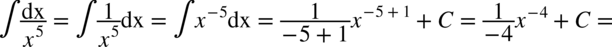
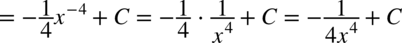
Korzystając z powyższego wzoru można też obliczać całki gdzie pojawiają się pierwiastki. Musimy tylko pamiętać o wzorach:

Warto też pamiętać, że 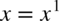 oraz
oraz 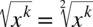 .
.
CAŁKA 27
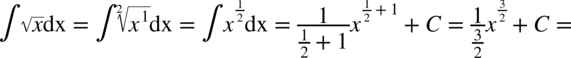
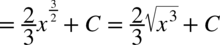
CAŁKA 28
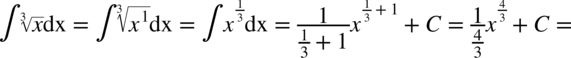
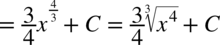
CAŁKA 29
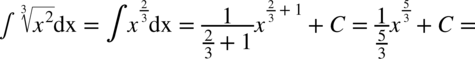
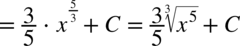
Korzystając z obydwu wzorów 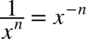 i
i 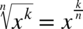 można obliczać następujące całki:
można obliczać następujące całki:
CAŁKA 30
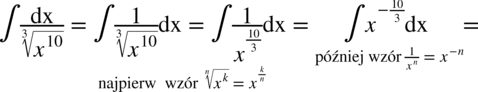
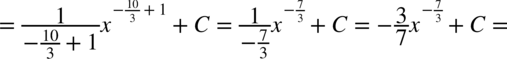
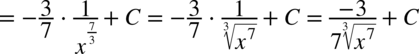
CAŁKA 31
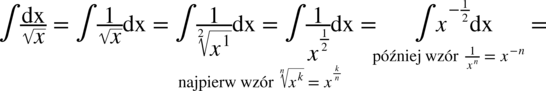
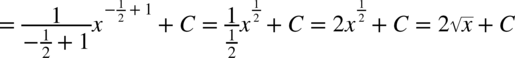
Oczywiście można zostawiać wynik w postaci potęgowej już w momencie kiedy pojawia się po raz pierwszy stała całkowania  , czyli
, czyli 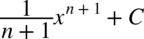 i jest on jak najbardziej poprawny , ale ja wychodzę z założenia, że należy go doprowadzić do najprostszej postaci i najlepiej takiej samej jak wyjściowa funkcja podcałkowa, a więc jeżeli na początku występowały pierwiastki, to w wyniku też będą pierwiastki, jeżeli na początku były potęgi, to w wyniku też będą potęgi.
i jest on jak najbardziej poprawny , ale ja wychodzę z założenia, że należy go doprowadzić do najprostszej postaci i najlepiej takiej samej jak wyjściowa funkcja podcałkowa, a więc jeżeli na początku występowały pierwiastki, to w wyniku też będą pierwiastki, jeżeli na początku były potęgi, to w wyniku też będą potęgi.
Kolejny wzór to 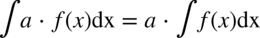 . Oznacza on, że przed znak całki można wyciągnąć stałą, która jest wymnożona przez funkcję podcałkową.
. Oznacza on, że przed znak całki można wyciągnąć stałą, która jest wymnożona przez funkcję podcałkową.
CAŁKA 32
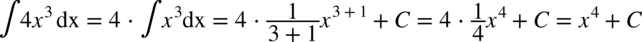
CAŁKA 33
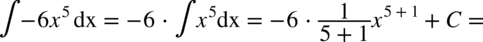
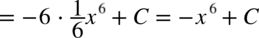
CAŁKA 34
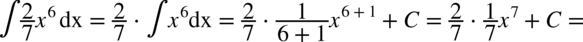
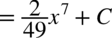
CAŁKA 35
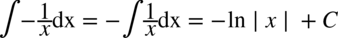
CAŁKA 36
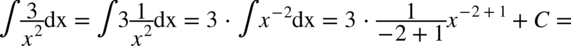
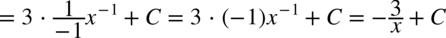
CAŁKA 37
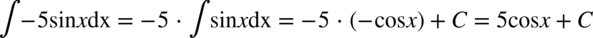
Jeżeli stała jest w mianowniku to nigdy „nie przeskoczy” do licznika tak jak w poniższych przykładach, zwracam na to uwagę, gdyż jest to jeden z najczęściej popełnianych błędów.
CAŁKA 38
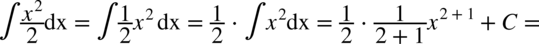
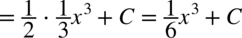
Jak widać 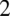 jest nadal w mianowniku.
jest nadal w mianowniku.
CAŁKA 39
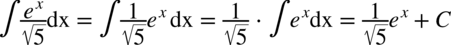
Podobnie jest z 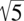 - nadal w mianowniku.
- nadal w mianowniku.
Kolejny przydatny wzór: 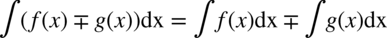
Dzięki tej własności rozbudowane całki można rozbijać na mniejsze całki, ale tylko wtedy kiedy poszczególne elementy funkcji podcałkowej są oddzielone od siebie znakiem 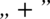 lub
lub  . Wymnożonych dwóch funkcji nie można rozdzielać ! Jako pojedynczą funkcję można rozumieć dowolne wyrażenie z
. Wymnożonych dwóch funkcji nie można rozdzielać ! Jako pojedynczą funkcję można rozumieć dowolne wyrażenie z 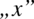 . Tak więc całka iloczynu nie jest równa iloczynowi całek !
. Tak więc całka iloczynu nie jest równa iloczynowi całek !
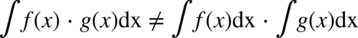
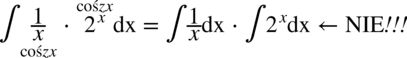
Przykłady:
CAŁKA 40
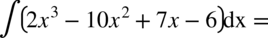
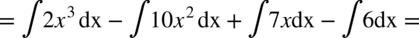
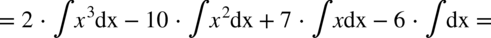
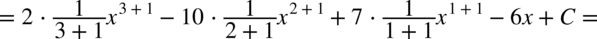
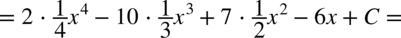
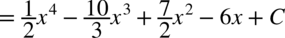
CAŁKA 41
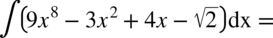
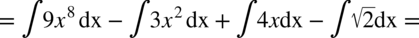
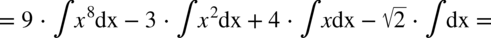
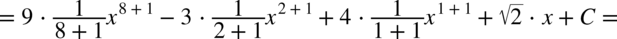
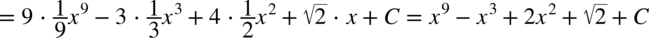
CAŁKA 42
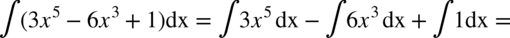
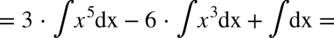
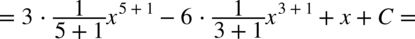
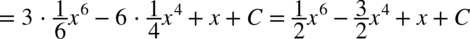
CAŁKA 43
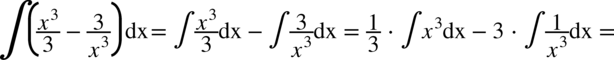
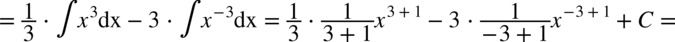
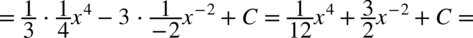
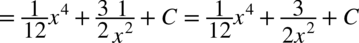
CAŁKA 44
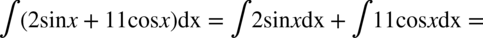
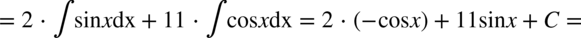
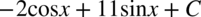
CAŁKA 45
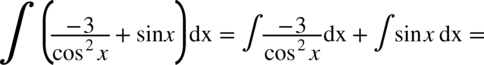
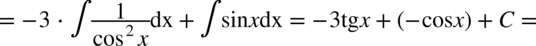
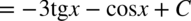
CAŁKA 46
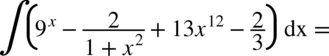
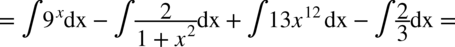
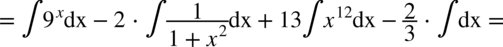
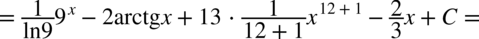
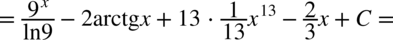
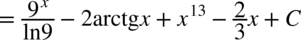
CAŁKA 47
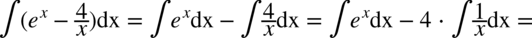
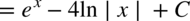
CAŁKA 48
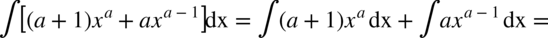
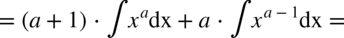
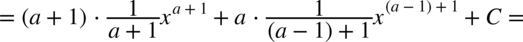
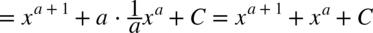
Można do każdej oddzielnie obliczonej całki dodawać stałą  , ale zostało przyjęte dla wygody, że pojawia się ona dopiero w ostatecznym wyniku.
, ale zostało przyjęte dla wygody, że pojawia się ona dopiero w ostatecznym wyniku.
Jeżeli ktoś spokojnie radzi sobie z liczeniem podstawowych całek nie musi pisać w rozwiązaniu wszystkich przejść, w prostszych całkach można od razu podawać wynik :).
Najważniejsze wzory i właściwości prostych całek nieoznaczonych zostały omówione. Poniżej przykłady ciekawszych całek wykorzystujących jedynie podstawowe wzory oraz umiejętności matematyczne.
W poniższych całkach wystarczy pozbyć się nawiasów wymnażając kolejne składniki:
CAŁKA 50
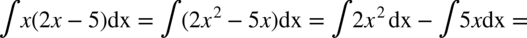
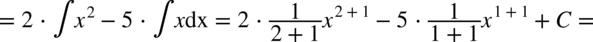
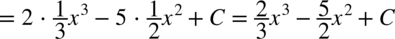
CAŁKA 51
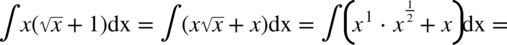
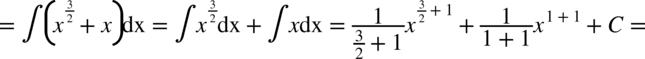
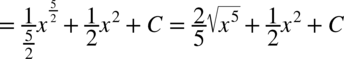
Korzystamy ze wzoru 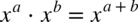 dlatego
dlatego 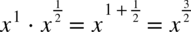
CAŁKA 52
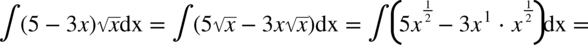
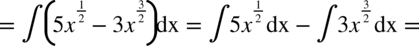
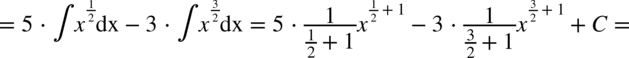
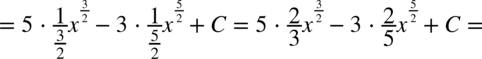
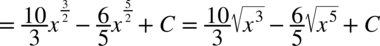
CAŁKA 53
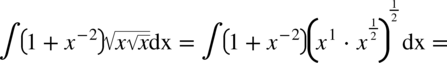
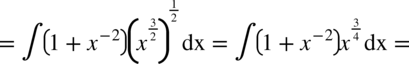
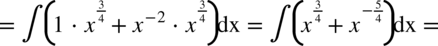
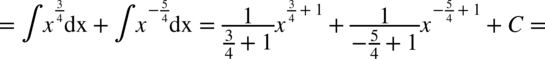
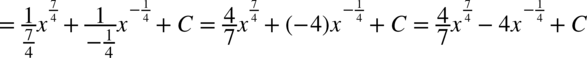
W tej całce najwygodniejsza okazała się zamiana pierwiastków na potęgi zanim pozbyliśmy się nawiasów.
Najpierw wzór 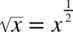 dlatego
dlatego 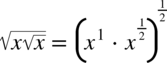 , później
, później 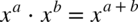 więc
więc 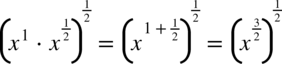 , na końcu wzór
, na końcu wzór 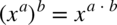 więc
więc 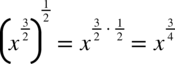
CAŁKA 54
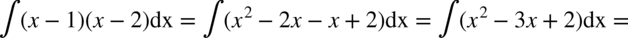
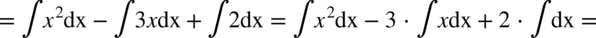
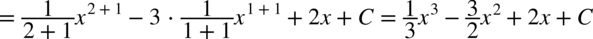
albo korzystając ze wzorów skróconego mnożenia:
CAŁKA 55
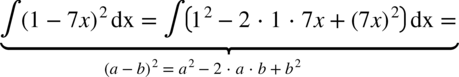
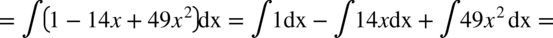
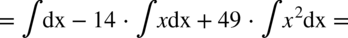

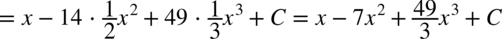
CAŁKA 56
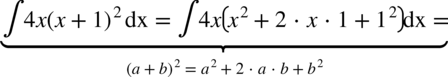
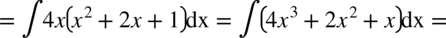
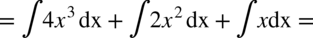
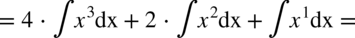
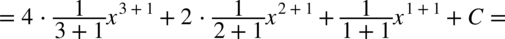
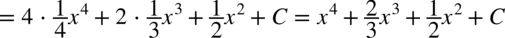
CAŁKA 57
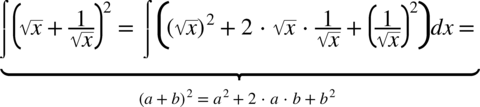
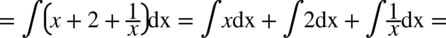
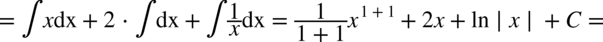
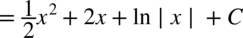
Jeżeli podnosimy pierwiastek do potęgi identycznej jak stopień tego pierwiastka to pierwiastek ulega redukcji, czyli „skasowaniu”.
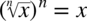 dlatego
dlatego 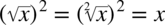
CAŁKA 58
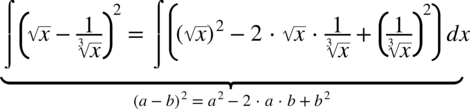
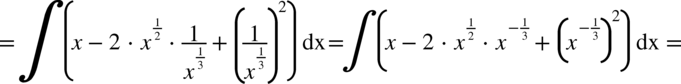
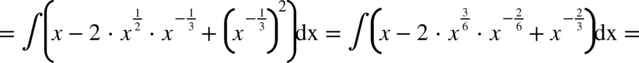
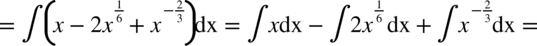
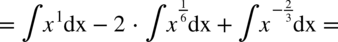
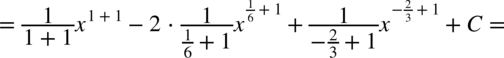
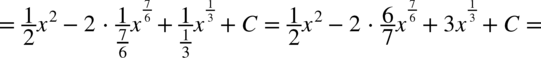
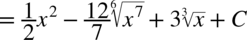
CAŁKA 59
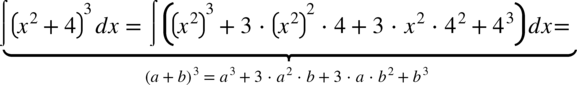
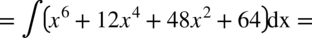
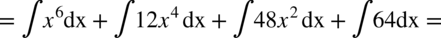
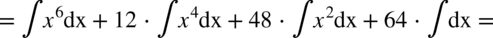
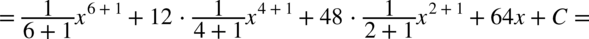
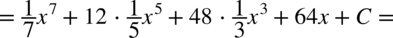
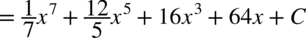
Pamiętamy przy podnoszeniu do potęgi, że 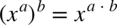 dlatego
dlatego 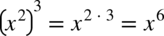 oraz
oraz 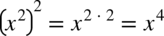
Teraz zajmijmy się całkami składającymi się wyłącznie z liczb, potęg i pierwiastków 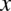 , w których występuje również kreska ułamkowa, a więc
, w których występuje również kreska ułamkowa, a więc 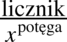 , ale w mianowniku nie ma ani dodawania ani odejmowania pomiędzy poszczególnymi składnikami tak jak w tym przykładzie:
, ale w mianowniku nie ma ani dodawania ani odejmowania pomiędzy poszczególnymi składnikami tak jak w tym przykładzie: 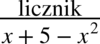 . Tego typu całki rozdziela się na mniejsze ułamki dzieląc każdy element licznika przez mianownik tak jak to można wykonać na prostych liczbach, przykładowo:
. Tego typu całki rozdziela się na mniejsze ułamki dzieląc każdy element licznika przez mianownik tak jak to można wykonać na prostych liczbach, przykładowo: 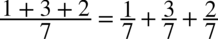
CAŁKA 60
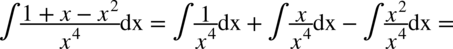
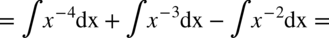
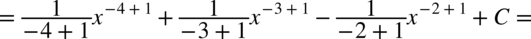
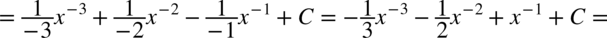
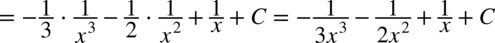
Korzystamy ze wzorów 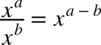 , także
, także 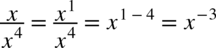 oraz
oraz 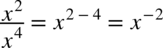
CAŁKA 61
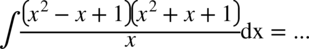
Najpierw wymnażamy nawiasy w liczniku, ponieważ pomiędzy nimi jest znak iloczynu, a jak pamiętamy całki iloczynu lub ilorazu dwóch funkcji nie można rozdzielić na iloczyn całek funkcji.
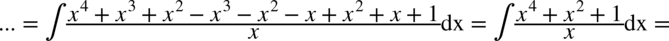
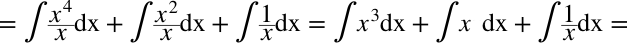
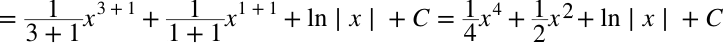
CAŁKA 62
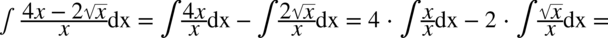
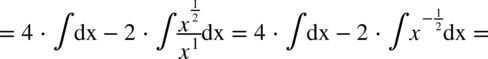
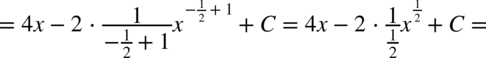
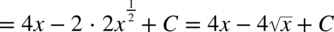
CAŁKA 63
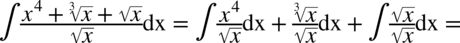
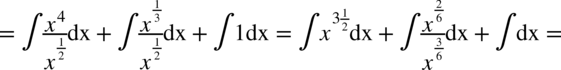
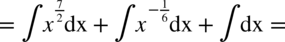
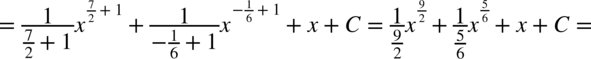
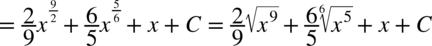
CAŁKA 64
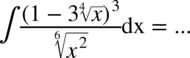
Najpierw pozbywamy się nawiasu w liczniku ułamka stosując wzór skróconego mnożenia 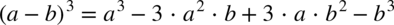
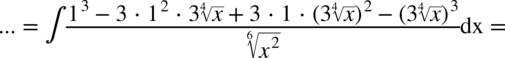
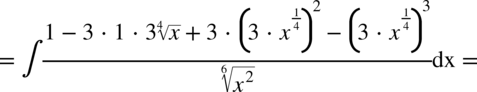
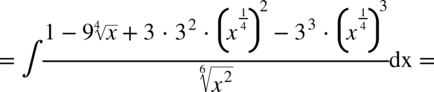
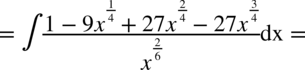
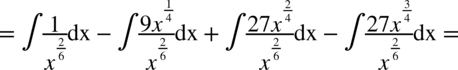
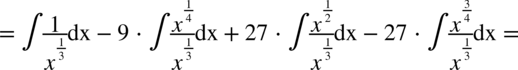
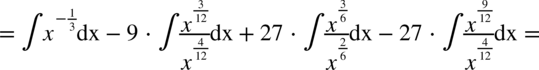
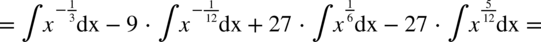
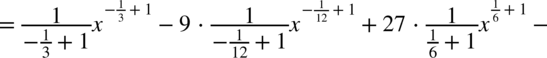
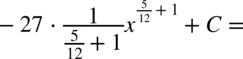
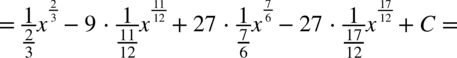
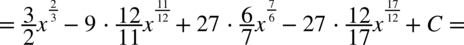
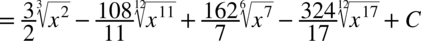
Korzystaliśmy z własności potęg 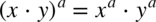 ,dlatego
,dlatego 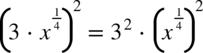 oraz
oraz 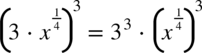
CAŁKA 65
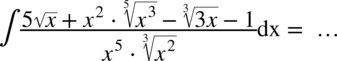
W mianowniku nadal nie występuje dodawanie ani odejmowanie, zatem można spokojnie rozdzielić ułamek na prostsze ułamki. Na początku dla wygody najlepiej zamienić pierwiastki na potęgi i tym samym uprościć poszczególne składniki.
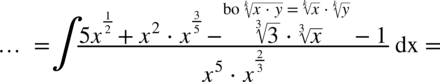
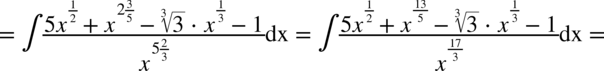
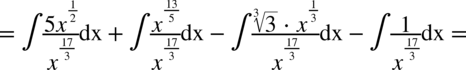
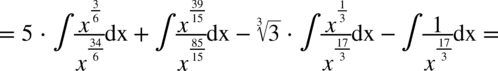
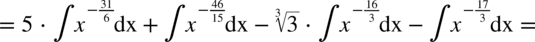
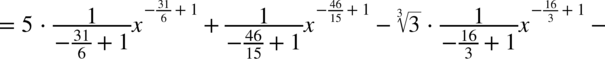
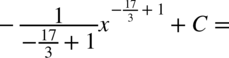
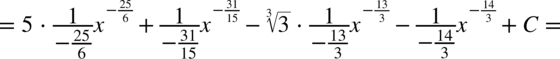
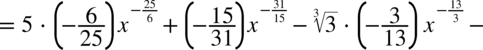
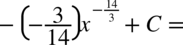
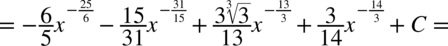
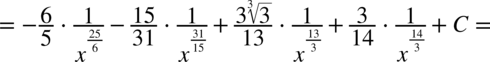
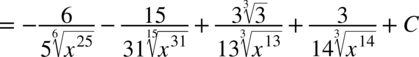
CAŁKA 66
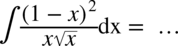
Tu postępujemy jak w poprzednim przykładzie – w mianowniku nie ma odejmowania ani dodawania. Na początku pozbywamy się nawiasu w liczniku wykorzystując wzór skróconego mnożenia: 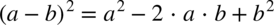
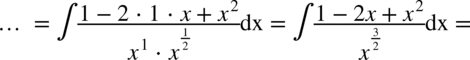
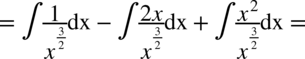
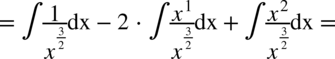
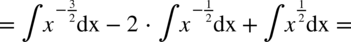
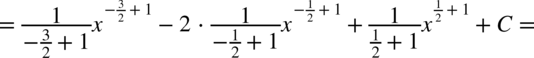
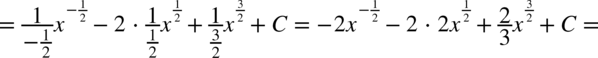
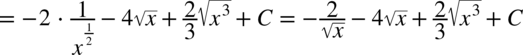
Teraz zajmijmy się całkami podobnymi do powyższych, ale w mianowniku będzie występować dodawanie lub odejmowanie np. 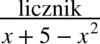 . Tego typu całki oblicza się stosując wzory skróconego mnożenia lub rozkładanie na czynniki i skracanie – dzięki temu całka się upraszcza i znika mianownik. Z reguły to licznik zostaje rozłożony na czynniki. Rozdzielanie na proste ułamki nie ma tu większego sensu, ponieważ i tak otrzymamy całki, których nie obliczy się przy pomocy podstawowych wzorów. Jeżeli rozkładanie na czynniki nie daje spodziewanego rezultatu czyli uproszczenia przykładu i tym samym nie jest możliwe zastosowanie podstawowych wzorów na obliczanie całek to kwalifikują się one do innych metod np. podstawiania lub obliczania całek funkcji wymiernych. Oto przykłady:
. Tego typu całki oblicza się stosując wzory skróconego mnożenia lub rozkładanie na czynniki i skracanie – dzięki temu całka się upraszcza i znika mianownik. Z reguły to licznik zostaje rozłożony na czynniki. Rozdzielanie na proste ułamki nie ma tu większego sensu, ponieważ i tak otrzymamy całki, których nie obliczy się przy pomocy podstawowych wzorów. Jeżeli rozkładanie na czynniki nie daje spodziewanego rezultatu czyli uproszczenia przykładu i tym samym nie jest możliwe zastosowanie podstawowych wzorów na obliczanie całek to kwalifikują się one do innych metod np. podstawiania lub obliczania całek funkcji wymiernych. Oto przykłady:
CAŁKA 67
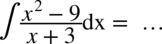
Spójrzmy na licznik całki. Mamy tu wzór skróconego mnożenia 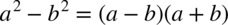 czyli
czyli 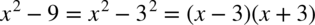 .
.
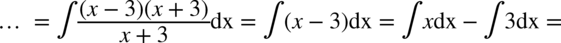
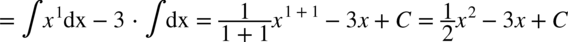
CAŁKA 68
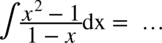
W liczniku znów jest wzór skróconego mnożenia 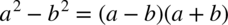 czyli
czyli 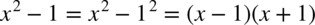 .
.
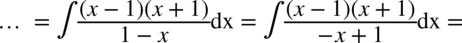
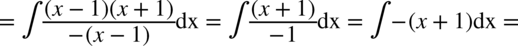
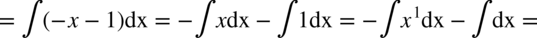
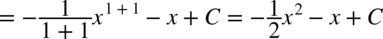
W mianowniku całki zmieniono jedynie kolejność składników i wyciągnięto minus przed nawias po to, aby bezproblemowo skrócić mianownik z licznikiem.
CAŁKA 69
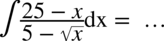
Na pierwszy rzut oka wydaje się, że w przykładzie nie ma żadnego wzoru skróconego mnożenia, jednak warto przyjrzeć się całości. W liczniku występuje wzór skróconego mnożenia 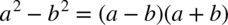 , a wygląda on następująco:
, a wygląda on następująco: 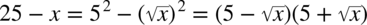 . Warto pamiętać
. Warto pamiętać 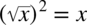 - podnosząc pierwiastek danego stopnia do potęgi równej stopniowi pierwiastka otrzymujemy wartość pod pierwiastkiem (pierwiastek się „kasuje”).
- podnosząc pierwiastek danego stopnia do potęgi równej stopniowi pierwiastka otrzymujemy wartość pod pierwiastkiem (pierwiastek się „kasuje”).
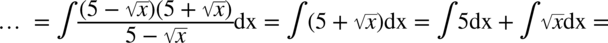
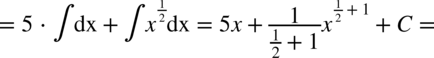
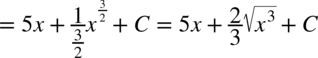
CAŁKA 70
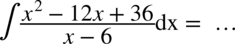
W liczniku znów występuje wzór skróconego mnożenia 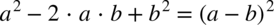 , czyli
, czyli 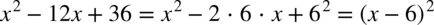 dzięki temu „zwijamy” licznik. Popoznawanie wzorów skróconego mnożenia znajdziesz tutaj.
dzięki temu „zwijamy” licznik. Popoznawanie wzorów skróconego mnożenia znajdziesz tutaj.
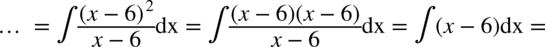
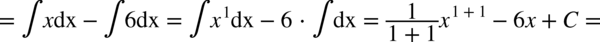
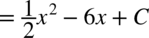
CAŁKA 71
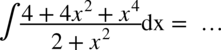
W liczniku występuje wzór skróconego mnożenia 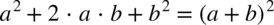 , czyli
, czyli 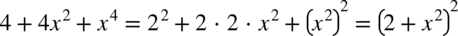 dzięki czemu licznik można „zwinąć”.
dzięki czemu licznik można „zwinąć”.
Rozpoznawanie wzorów skróconego mnożenia znajdziesz tutaj.
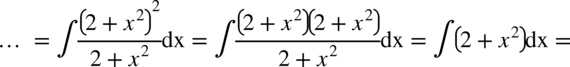
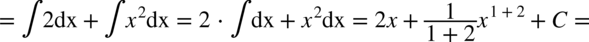
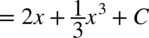
CAŁKA 72
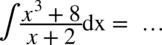
W tym przykładzie w liczniku ponownie mamy do czynienia ze wzorem skróconego mnożenia. Tym razem ma on postać 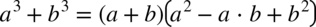 , tak więc
, tak więc 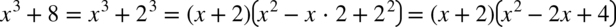
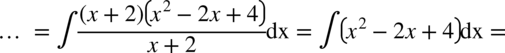
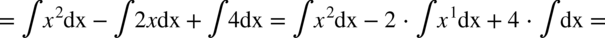
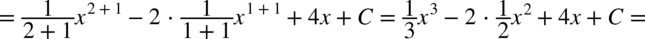
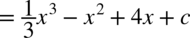
CAŁKA 73
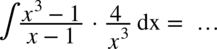
W liczniku ponownie mamy do czynienia ze wzorem skróconego mnożenia postaci 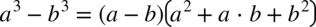 , a więc
, a więc 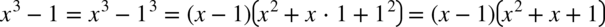
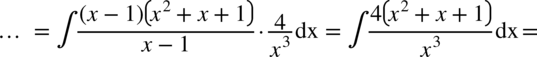
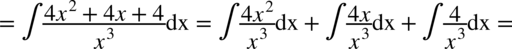
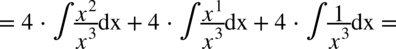
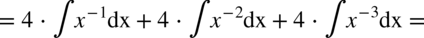
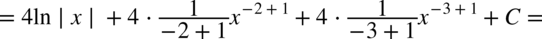
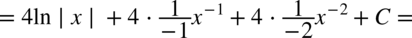
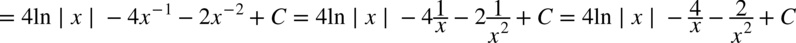
CAŁKA 74
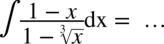
Tu również w liczniku występuje wzór skróconego mnożenia 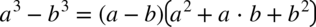 , tylko jest on nieco bardziej zakamuflowany. Przyglądając się bliżej mianownikowi można dojść do takiego wniosku:
, tylko jest on nieco bardziej zakamuflowany. Przyglądając się bliżej mianownikowi można dojść do takiego wniosku:
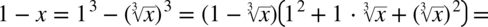
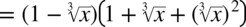
Jeszcze raz przypominam, że pierwiastek znika przy podnoszeniu składnika to potęgi równej stopniowi pierwiastka: 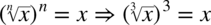
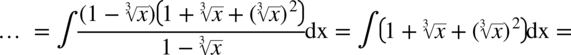
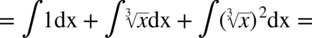
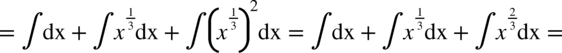
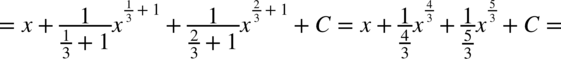
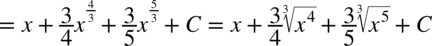
CAŁKA 75
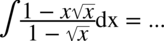
W tej całce nie widać ani wzorów skróconego mnożenia ani innych charakterystycznych cech dzięki czemu można ją uprościć. W mianowniku jest odejmowanie, więc nie ma sensu rozkładać jej na prostsze ułamki. Zapiszmy pierwiastki w postaci potęg i maksymalnie je uprośćmy:
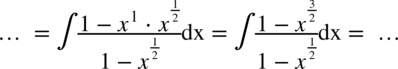
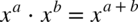 daje
daje 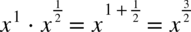
Teraz znów przyjrzymy się licznikowi, gdyby nie 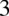 w potędze
w potędze 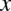 to licznik wyglądałby identycznie jak mianownik. Spróbujmy pozbyć się tej
to licznik wyglądałby identycznie jak mianownik. Spróbujmy pozbyć się tej 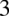 .
.
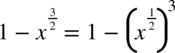 , bo
, bo 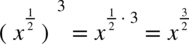 ze wzoru
ze wzoru 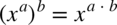
Co ciekawe można pójść dalej 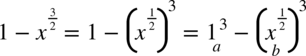 i dzięki temu znów otrzymujemy wzór skróconego mnożenia
i dzięki temu znów otrzymujemy wzór skróconego mnożenia 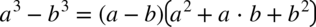 .
.
Rozłożenie wyrażenia wygląda następująco:
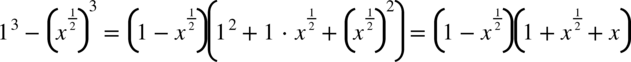
Wracamy do całki:
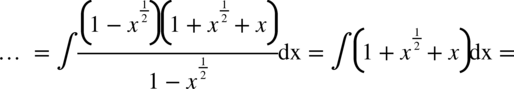
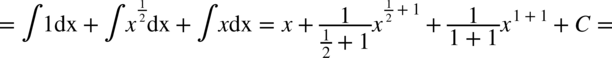
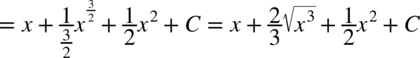
W kolejnych kilku całkach będziemy rozkładać licznik na czynniki obliczając deltę 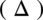 i pierwiastki wielomianu, dzięki temu pozbędziemy się mianownika i skorzystamy z podstawowych wzorów na całki. Jeżeli mianownik nie ulegnie zredukowaniu to w zależności od przykładu należy rozwiązywać metodą podstawiania lub całek funkcji wymiernych.
i pierwiastki wielomianu, dzięki temu pozbędziemy się mianownika i skorzystamy z podstawowych wzorów na całki. Jeżeli mianownik nie ulegnie zredukowaniu to w zależności od przykładu należy rozwiązywać metodą podstawiania lub całek funkcji wymiernych.
CAŁKA 76
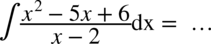
W liczniku nie ma wzoru skróconego mnożenia (sprawdzisz tutaj rozpoznawanie wzorów skróconego mnożenia). Największą potęgą jest 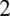 , zatem obliczamy deltę
, zatem obliczamy deltę 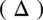 i pierwiastki w celu zamiany postaci ogólnej trójmianu kwadratowego
i pierwiastki w celu zamiany postaci ogólnej trójmianu kwadratowego 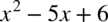 na postać iloczynową.
na postać iloczynową.
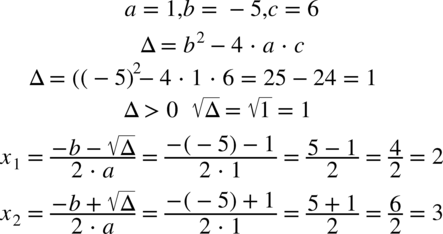
Postać iloczynowa przy 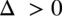 wygląda następująco:
wygląda następująco: 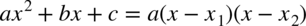 , zatem
, zatem 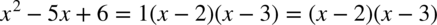 .
.
Wracamy do całki:
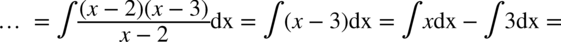
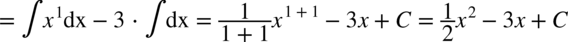
CAŁKA 77
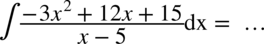
W liczniku nie ma wzoru skróconego mnożenia (sprawdzisz tutaj rozpoznawanie wzorów skróconego mnożenia). Największą potęgą jest 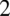 , zatem obliczamy deltę
, zatem obliczamy deltę 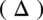 i pierwiastki w celu zamiany postaci ogólnej
i pierwiastki w celu zamiany postaci ogólnej 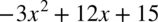 trójmianu kwadratowego na postać iloczynową.
trójmianu kwadratowego na postać iloczynową.
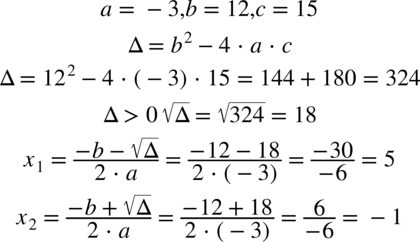
Postać iloczynowa przy 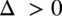 wygląda następująco:
wygląda następująco: 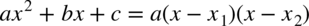 , zatem
, zatem 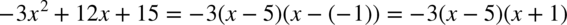 .
.
Wracamy do całki:
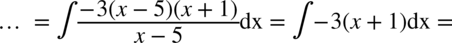
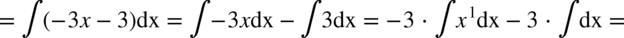
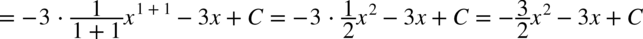
CAŁKA 78
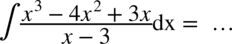
W liczniku nie ma wzoru skróconego mnożenia (sprawdzisz tutaj rozpoznawanie wzorów skróconego mnożenia). Największą potęgą jest 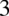 , więc nie możemy obliczyć delty
, więc nie możemy obliczyć delty 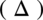 , ale przyjrzyjmy się jeszcze raz dokładnie licznikowi. Przy każdym składniku jest
, ale przyjrzyjmy się jeszcze raz dokładnie licznikowi. Przy każdym składniku jest 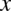 , zatem można wyciągnąć go przed nawias, a w nawiasie pojawi się funkcja kwadratowa:
, zatem można wyciągnąć go przed nawias, a w nawiasie pojawi się funkcja kwadratowa:
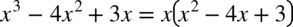
Zamieniamy postać ogólną 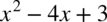 trójmianu kwadratowego na postać iloczynową.
trójmianu kwadratowego na postać iloczynową.
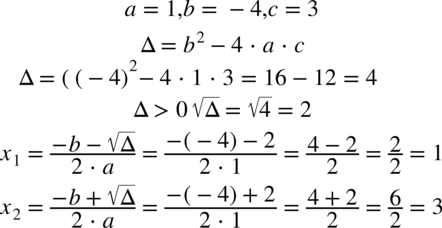
Postać iloczynowa przy 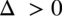 wygląda następująco:
wygląda następująco: 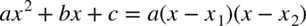 , zatem
, zatem 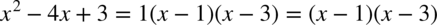 .
.
Ostatecznie 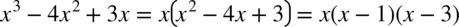
Wracamy do całki:
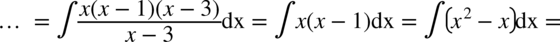
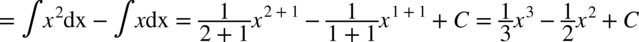
CAŁKA 79
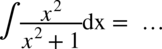
Korzystamy z następującej sztuczki:
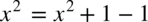
Jeżeli do dowolnego wyrażenia dodam konkretną liczbę i następnie ją odejmę to wartość wyrażenia nie ulegnie zmianie.
Aby nie było wątpliwości 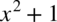 nie jest wzorem skróconego mnożenia ! Pomiędzy składnikami musi być znak
nie jest wzorem skróconego mnożenia ! Pomiędzy składnikami musi być znak  .
.
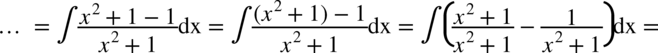
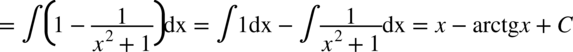
Na końcu zastosowano podstawowy wzór:
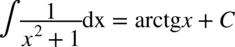
CAŁKA 80
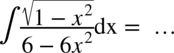
Całka o dość specyficznym charakterze, ponieważ pojawia się w niej pierwiastek nad całym wyrażeniem 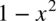 , a nie tylko nad
, a nie tylko nad 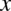 . Przyjrzyjmy się mianownikowi - liczba
. Przyjrzyjmy się mianownikowi - liczba 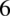 aż się prosi, aby ją wyciągnąć przed nawias.
aż się prosi, aby ją wyciągnąć przed nawias.
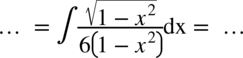
W mianowniku pojawił się identyczny wielomian jak w liczniku. Warto pamiętać, że każdy znak, wielomian można zapisać w postaci 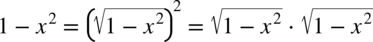 , ponieważ podniesienie pierwiastka do potęgi o tym samym stopniu co pierwiastek kasuje ten pierwiastek
, ponieważ podniesienie pierwiastka do potęgi o tym samym stopniu co pierwiastek kasuje ten pierwiastek 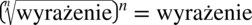 .
.
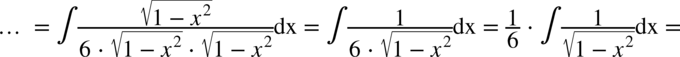
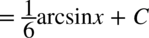
Na końcu zastosowano podstawowy wzór:
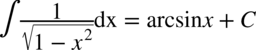
Teraz kilka przykładów ciekawszych całek, w których pojawia się funkcja wykładnicza postaci 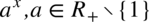 , czyli
, czyli 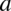 jest dowolną liczbą dodatnią, ale bez
jest dowolną liczbą dodatnią, ale bez 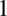 podniesioną do potęgi
podniesioną do potęgi 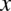 .
.
CAŁKA 81
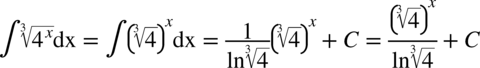
Warto pamiętać, że 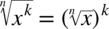 ,
,
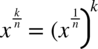 ze wzoru
ze wzoru 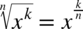
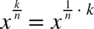 ze wzoru
ze wzoru 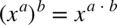
następnie 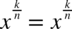 także obie strony są sobie równe.
także obie strony są sobie równe.
Także ze wzoru 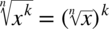 mamy
mamy 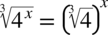
Na koniec ze skorzystaliśmy ze wzoru 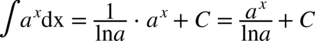 , gdzie
, gdzie 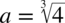 .
.
CAŁKA 82
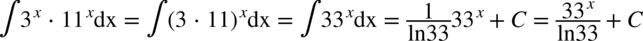
W powyższym przykładzie wystarczyło skorzystać z własności potęg 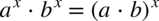 , dlatego
, dlatego 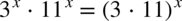 .
.
CAŁKA 83
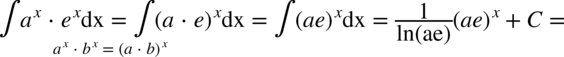
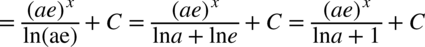
Korzystamy z własności logarytmów 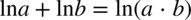 dlatego
dlatego 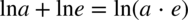 .
.
Również 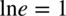 , ponieważ zapis logarytmu naturalnego
, ponieważ zapis logarytmu naturalnego 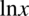 jest równoważny zapisowi
jest równoważny zapisowi 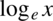 .
.
Tak więc 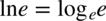 , a trzymając się definicji logarytmu
, a trzymając się definicji logarytmu 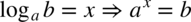 musimy odpowiedzieć na pytanie do której potęgi należy podnieść liczbę
musimy odpowiedzieć na pytanie do której potęgi należy podnieść liczbę 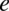 aby otrzymać liczbę
aby otrzymać liczbę 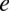 , tą potęgą jest
, tą potęgą jest 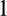 .
.
CAŁKA 84
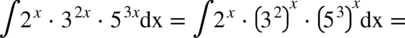
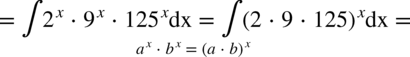
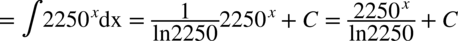
Należy pamiętać, że 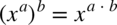 więc
więc 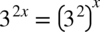 oraz
oraz 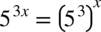 .
.
CAŁKA 85
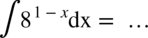
Całka wydaje się prosta i już chciałoby się od razu skorzystać ze wzoru 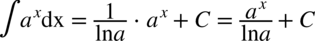 , ale ale wykładnik potęgi to
, ale ale wykładnik potęgi to 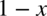 , a nie tylko
, a nie tylko 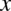 , wobec tego trzeba dokonać odpowiednich przekształceń aby uzyskać tylko sam
, wobec tego trzeba dokonać odpowiednich przekształceń aby uzyskać tylko sam 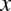 w tym wykładniku.
w tym wykładniku.
Na początku rozdzielmy elementy wykładnika zgodnie ze wzorem 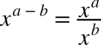 i wyciągając stałą przed znak całki:
i wyciągając stałą przed znak całki:
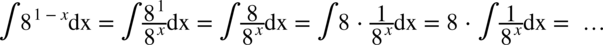
Kolejne przekształcenie to „nałożenie” danej potęgi 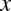 na licznik całki, a więc
na licznik całki, a więc 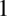 , aby doprowadzić funkcję podcałkową to postaci
, aby doprowadzić funkcję podcałkową to postaci 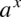 (teraz mamy
(teraz mamy 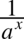 ). Akurat z tym nie ma problemu, ponieważ liczba
). Akurat z tym nie ma problemu, ponieważ liczba 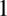 podniesiona do jakiejkolwiek potęgi zawsze daje
podniesiona do jakiejkolwiek potęgi zawsze daje 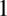 , także
, także 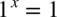 .
.
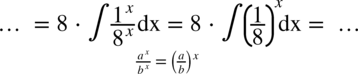
Korzystamy z podstawowego wzoru na całki 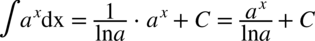 l gdzie
l gdzie 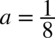 :
:
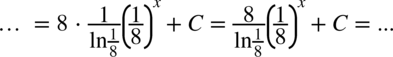
Właściwie już otrzymaliśmy wynik, można jeszcze przekształcić go do prostszej postaci korzystając ze wzoru 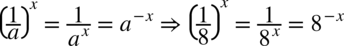 oraz z własności logarytmów
oraz z własności logarytmów 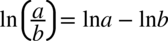 dlatego
dlatego 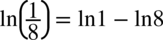 .
.
Również 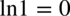 , ponieważ zapis logarytmu naturalnego
, ponieważ zapis logarytmu naturalnego 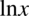 jest równoważny zapisowi
jest równoważny zapisowi 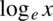 .
.
Tak więc 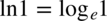 , a trzymając się definicji logarytmu
, a trzymając się definicji logarytmu 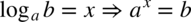 musimy odpowiedzieć na pytanie do której potęgi należy podnieść liczbę
musimy odpowiedzieć na pytanie do której potęgi należy podnieść liczbę 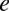 aby otrzymać liczbę
aby otrzymać liczbę 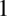 , tą potęgą jest
, tą potęgą jest 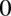 (każda liczba podniesiona do potęgi
(każda liczba podniesiona do potęgi 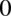 wynosi
wynosi 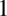 ).
).
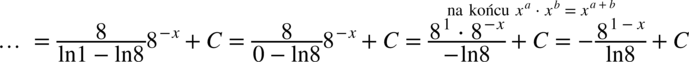
Tą całkę można też obliczyć stosując metodę podstawiania.
CAŁKA 86
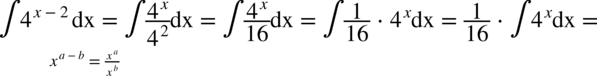
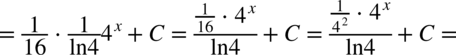
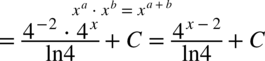
Tą całkę można też obliczyć stosując metodę podstawiania.
CAŁKA 87
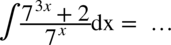
W mianowniku całki występuje tylko jeden element, zatem bezproblemowo można rozdzielić funkcję podcałkową na dwa oddzielne ułamki i tym samym na dwie całki:
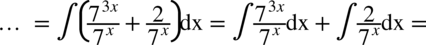
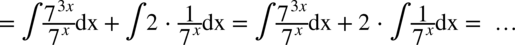
Teraz należy doprowadzić obie funkcje podcałkowe do postaci 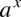 (czyli z dwóch liczb podniesionych do potęgi
(czyli z dwóch liczb podniesionych do potęgi 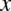 otrzymujemy jedną) wykonując operacje na potęgach:
otrzymujemy jedną) wykonując operacje na potęgach:
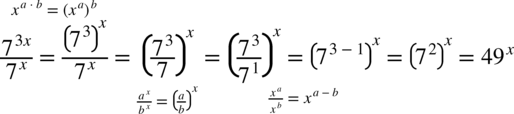
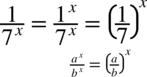 oczywiście pamiętamy, że
oczywiście pamiętamy, że 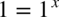
Wracamy do całki:
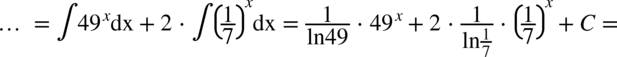
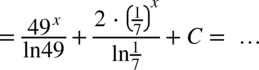
Wynik jest już prawidłowy, ale można jeszcze go przekształcić. Na początku zapiszmy o ile to możliwe wszystkie liczby jako potęgi 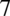 :
:
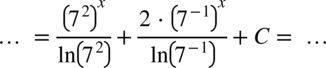
Teraz skorzystamy z własności potęg i logarytmów
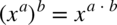 więc
więc 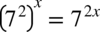 oraz
oraz 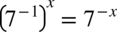
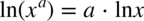 więc
więc 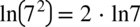 oraz
oraz 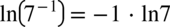
i sprowadzimy oba ułamki do wspólnego mianownika
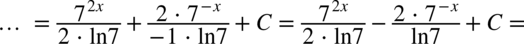
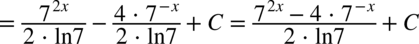
CAŁKA 88
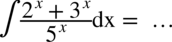
W mianowniku znów występuje tylko jeden składnik (nie ma dodawania ani odejmowania kilku elementów w mianowniku)– można zatem rozdzielić funkcję podcałkową na dwa ułamki:
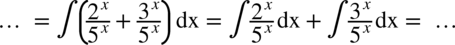
Korzystając z własności potęg 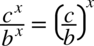 otrzymujemy postać
otrzymujemy postać 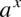 (czyli z dwóch liczb podniesionych do potęgi
(czyli z dwóch liczb podniesionych do potęgi 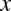 otrzymujemy jedną), dzięki której możemy już bezpośrednio korzystać ze wzoru
otrzymujemy jedną), dzięki której możemy już bezpośrednio korzystać ze wzoru 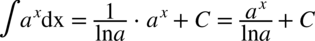 :
:
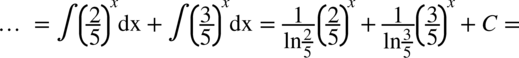
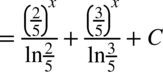
CAŁKA 89
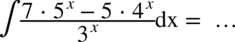
Na początku rozdzielamy funkcję podcałkową na dwa ułamki (możemy tak uczynić i ma to sens, ponieważ w mianowniku nie ma dodawania ani odejmowania) i wyciągamy stałą przed znak całki:
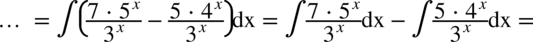
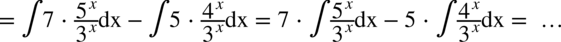
Korzystając z własności potęg 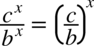 otrzymujemy postać
otrzymujemy postać 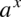 (czyli z dwóch liczb podniesionych do potęgi
(czyli z dwóch liczb podniesionych do potęgi 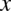 otrzymujemy jedną), dzięki której możemy już bezpośrednio korzystać ze wzoru
otrzymujemy jedną), dzięki której możemy już bezpośrednio korzystać ze wzoru 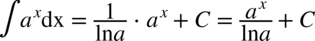 :
:
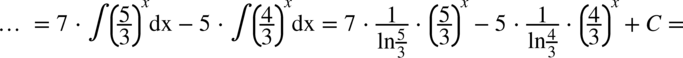
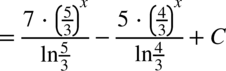
CAŁKA 90
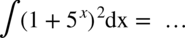
W tym przykładzie należy skorzystać ze wzoru skróconego mnożenia 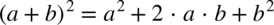 i właściwości potęg
i właściwości potęg 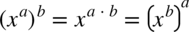 :
:
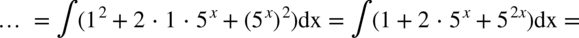
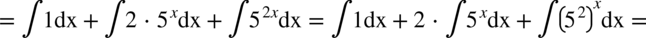
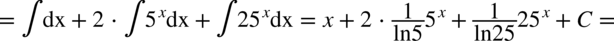
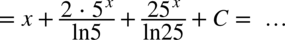
Całka jest już obliczona, ale można ją zapisać w nieco innej postaci. Na początku zapiszmy o ile to możliwe wszystkie liczby jako potęgi 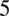 :
:
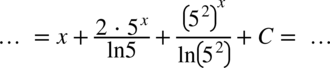
Skorzystajmy z własności potęg i logarytmów:
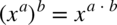 więc
więc 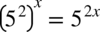 oraz
oraz
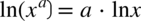 więc
więc 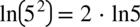 i sprowadzimy oba ułamki do wspólnego mianownika:
i sprowadzimy oba ułamki do wspólnego mianownika:
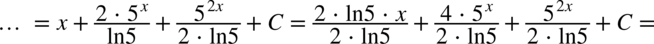
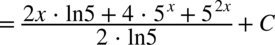
CAŁKA 91
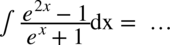
W danej całce rozdzielanie funkcji podcałkowej na dwa ułamki nie ma większego sensu, ponieważ w mianowniku występuje znak dodawania pomiędzy składnikami. Spójrzmy na licznik – jest tu ukryty wzór skróconego mnożenia 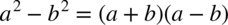 , rozłóżmy go na czynniki zgodnie z podanym wzorem pamiętając również o właściwościach potęg
, rozłóżmy go na czynniki zgodnie z podanym wzorem pamiętając również o właściwościach potęg 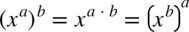 . Następnie skracamy mianownik z licznikiem:
. Następnie skracamy mianownik z licznikiem:
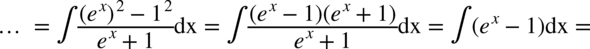
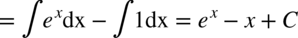
CAŁKA 92
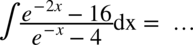
W tej całce znów mamy identyczną sytuację jak w poprzednim przykładzie. W liczniku występuje wzór skróconego mnożenia 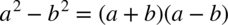 , można go zauważyć po skorzystaniu z własności potęg
, można go zauważyć po skorzystaniu z własności potęg 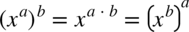 . Następnie skracamy mianownik z licznikiem:
. Następnie skracamy mianownik z licznikiem:
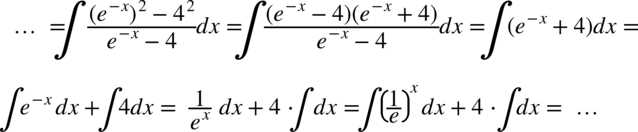
W przykładzie skorzystaliśmy z własności potęg 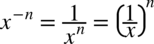 dlatego też
dlatego też 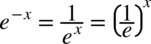 . Dzięki temu zapisowi możemy używać wzoru
. Dzięki temu zapisowi możemy używać wzoru 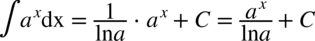 , gdzie
, gdzie 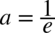 . Nie mogliśmy skorzystać bezpośrednio ze wzoru
. Nie mogliśmy skorzystać bezpośrednio ze wzoru 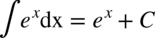 , ponieważ w wykładniku potęgi był minus, a we wzorze minus nie występuje. Oczywiście licząc całkę z
, ponieważ w wykładniku potęgi był minus, a we wzorze minus nie występuje. Oczywiście licząc całkę z 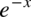 można skorzystać z metody podstawiania, która zdecydowanie szybciej daje wynik, ale w tym dziale zakładam, że jeszcze jej nie znamy. Wracamy do całki:
można skorzystać z metody podstawiania, która zdecydowanie szybciej daje wynik, ale w tym dziale zakładam, że jeszcze jej nie znamy. Wracamy do całki:
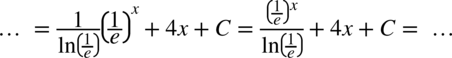
Znów zapiszmy 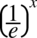 jako
jako 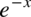 oraz
oraz 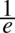 jako
jako 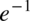 i na końcu skorzystajmy z własności logarytmów
i na końcu skorzystajmy z własności logarytmów 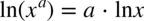 czyli
czyli 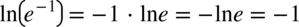 (
(  do jakiej potęgi należy podnieść liczbę
do jakiej potęgi należy podnieść liczbę  aby otrzymać
aby otrzymać 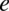 ) aby maksymalnie uprościć wynik:
) aby maksymalnie uprościć wynik:
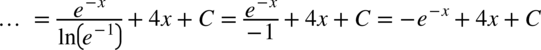
CAŁKA 93
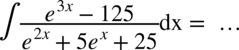
W mianowniku pomiędzy składnikami znów występuje plus, więc nie ma sensu rozkładać funkcji podcałkowej na mniejsze ułamki. W liczniku znów występuje wzór skróconego mnożenia w postaci 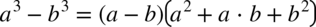 . Można go zauważyć gdy skorzystamy z własności potęg
. Można go zauważyć gdy skorzystamy z własności potęg 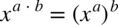 i po rozłożeniu licznika na czynniki możemy całkowicie pozbyć się mianownika skracając go z licznikiem:
i po rozłożeniu licznika na czynniki możemy całkowicie pozbyć się mianownika skracając go z licznikiem:
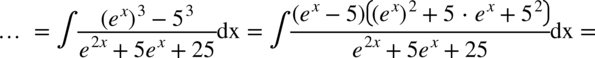
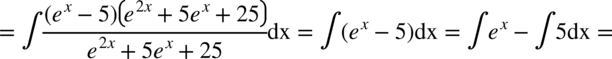
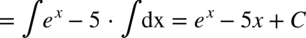
Teraz kilka całek, w których występują funkcje trygonometryczne i można je rozwiązać wykorzystując jedynie podstawowe wzory.
CAŁKA 94
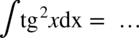
Pamiętamy, że:
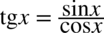
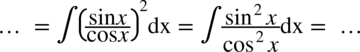
Korzystamy z „jedynki” trygonometrycznej odpowiednio dokonując przekształceń w liczniku
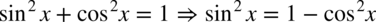
i rozdzielamy funkcję podcałkową na dwa ułamki. Na końcu korzystamy ze wzoru na całkę:
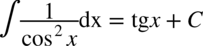
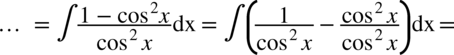
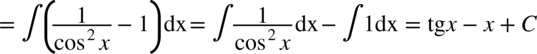
CAŁKA 95
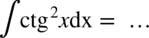
Na początku wykorzystujemy wzór:
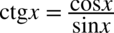
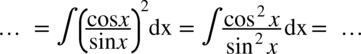
Korzystamy z „jedynki” trygonometrycznej odpowiednio dokonując przekształceń w liczniku
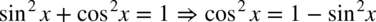
i rozdzielamy funkcję podcałkową na dwa ułamki. Na końcu korzystamy ze wzoru na całkę:
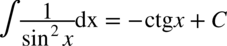
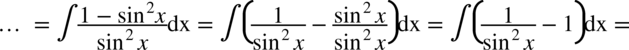
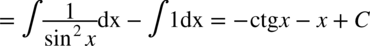
CAŁKA 96
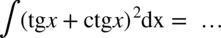
Zaczynamy od rozpisania funkcji podcałkowej ze wzoru skróconego mnożenia 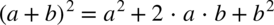 :
:
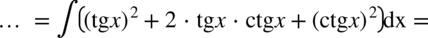
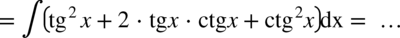
Skorzystamy teraz z własności funkcji trygonometrycznych. Dla każdego kąta zachodzi 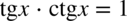 , zatem:
, zatem:
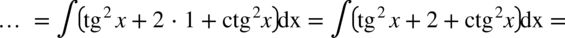
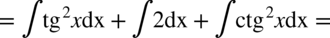
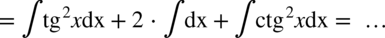
Całka 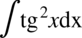 oraz
oraz 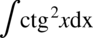 zostały już wcześniej obliczone (całka 94 i 95) zatem skorzystamy już z gotowych wyników.
zostały już wcześniej obliczone (całka 94 i 95) zatem skorzystamy już z gotowych wyników.
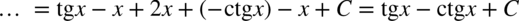
CAŁKA 97
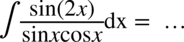
W tej całce korzystamy ze wzoru na sinus podwojonego kąta 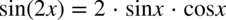 , zatem:
, zatem:
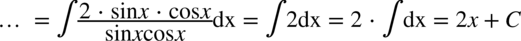
CAŁKA 98
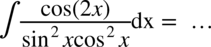
Należy skorzystać ze wzoru na cosinus podwójnego kąta 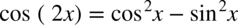 i rozdzielić funkcję podcałkową na dwa ułamki. Na samym końcu korzystamy ze wzorów
i rozdzielić funkcję podcałkową na dwa ułamki. Na samym końcu korzystamy ze wzorów 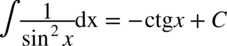 oraz
oraz 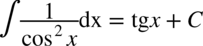 .
.
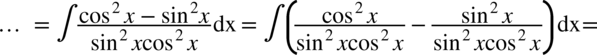
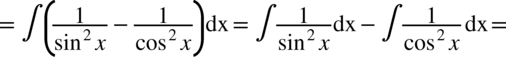
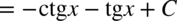
CAŁKA 99
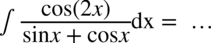
Tu również na początku skorzystam ze wzoru na cosinus podwojonego kąta 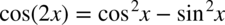 :
:
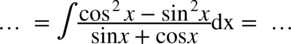
Rozdzielanie funkcji podcałkowej na dwa ułamki nie ma sensu, ponieważ w mianowniku występuje dodawanie, ale warto przyjrzeć się licznikowi, mamy tu wzór skróconego mnożenia w postaci 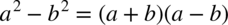 i dzięki temu można rozpisać licznik na iloczyn dwóch nawiasów co pozwala na skrócenie mianownika:
i dzięki temu można rozpisać licznik na iloczyn dwóch nawiasów co pozwala na skrócenie mianownika:
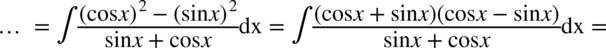
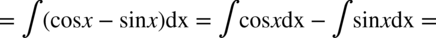
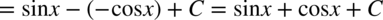
Dla przypomnienia 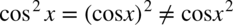 , podobnie
, podobnie 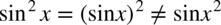 .
.