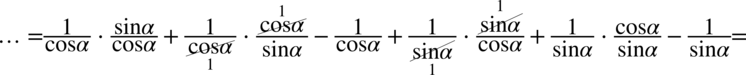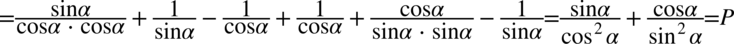Przykład 33
[kliknij aby rozwinąć] 
Założenie: 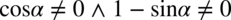 (żaden z mianowników nie może być równy 0). Po przekształceniu założenia otrzymujemy
(żaden z mianowników nie może być równy 0). Po przekształceniu założenia otrzymujemy  .
.
W tym przykładzie obie strony równości są podobnej długości, nie występuje tu ani tangens ani cotangens, nie widać też śladów przekształconej jedynki trygonometrycznej 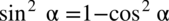 ,
, 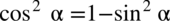 , ponieważ nie występuje ani sinus ani cosinus do kwadratu, co prawda można skorzystać
, ponieważ nie występuje ani sinus ani cosinus do kwadratu, co prawda można skorzystać 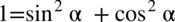 i rozłożyć
i rozłożyć  , ale to i tak nic nie da. Podobnie nic nie uzyskamy rozkładając lewą stronę na dwa mniejsze ułamki
, ale to i tak nic nie da. Podobnie nic nie uzyskamy rozkładając lewą stronę na dwa mniejsze ułamki 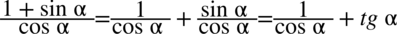 . W tym przypadku trzeba wykonać pewien trik. Przedstawię tu dwa sposoby:
. W tym przypadku trzeba wykonać pewien trik. Przedstawię tu dwa sposoby:
I sposób (nieco łatwiejszy)
Będziemy przekształcać prawą stronę i zaczniemy od wymnożenia mianownika przez to samo wyrażenie, które się w nim znajduje, ale z przeciwnym znakiem czyli 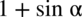 . Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie.
. Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie.
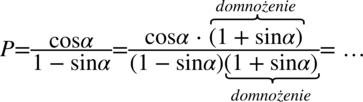
Po wymnożeniu mianownika okaże się, że otrzymujemy przekształcenie jedynki trygonometrycznej, co znacznie ułatwi sprawę. Nawiasy w mianowniku różnią się znakiem pośrodku, także skorzystam ze wzoru skróconego mnożenia 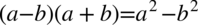 (wynik będzie identyczny jeśli zdecydujemy się na „zwyczajne” wymnożenie nawiasów, ale jest to sposób bardziej pracochłonny):
(wynik będzie identyczny jeśli zdecydujemy się na „zwyczajne” wymnożenie nawiasów, ale jest to sposób bardziej pracochłonny):
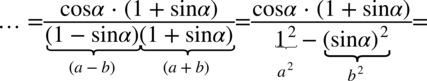
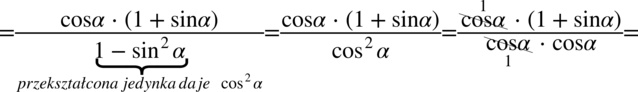


Jak widać w liczniku nie pozbywaliśmy się nawiasów. Był to specjalny zabieg w celu skrócenia cosinusa z licznika z cosinusem z mianownika. Jeżeli zbyt wcześnie pozbylibyśmy się nawiasów w liczniku nie zauważylibyśmy możliwości późniejszego skracania.
II sposób
Tym razem będziemy przekształcać lewą stronę i zaczniemy od wymnożenia mianownika przez cosinus w celu otrzymania cosinusa do kwadratu, a co za tym idzie da to nam możliwość skorzystania z przekształconej jedynki trygonometrycznej, bo 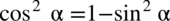 . Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie, także licznik również zostanie wymnożony przez cosinus.
. Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie, także licznik również zostanie wymnożony przez cosinus.

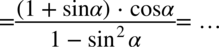
Kolejny etap stanowi rozłożenie mianownika ze wzoru skróconego mnożenia
 , ponieważ wyrażenie z mianownika
, ponieważ wyrażenie z mianownika
 można rozpisać
można rozpisać
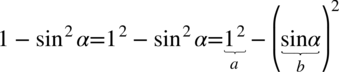 i wyłowić
i wyłowić
 oraz
oraz
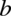 :
:

Dodawanie jest zamknięte w nawiasach, zatem można skrócić identyczne nawiasy z licznika i mianownika:
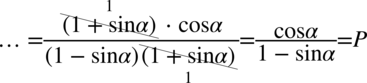

Jak widać licznik nie był celowo wymnażany w celu skrócenia go z identycznym nawiasem z mianownika.
Przykład 34
[kliknij aby rozwinąć] 
Założenie: 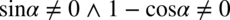 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 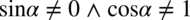 .
.
W tym przykładzie obie strony równości są podobnej długości, nie występuje tu ani tangens ani cotangens, nie widać też śladów przekształconej jedynki trygonometrycznej 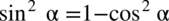 ,
, 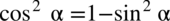 , ponieważ nie występuje ani sinus ani cosinus do kwadratu, co prawda można skorzystać
, ponieważ nie występuje ani sinus ani cosinus do kwadratu, co prawda można skorzystać 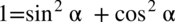 i rozłożyć
i rozłożyć  , ale to i tak nic nie da. Podobnie nic nie uzyskamy rozkładając lewą stronę na dwa mniejsze ułamki
, ale to i tak nic nie da. Podobnie nic nie uzyskamy rozkładając lewą stronę na dwa mniejsze ułamki 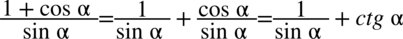 . W tym przypadku trzeba wykonać pewien trik. Przedstawię tu dwa sposoby:
. W tym przypadku trzeba wykonać pewien trik. Przedstawię tu dwa sposoby:
I sposób (nieco łatwiejszy)
Będziemy przekształcać prawą stronę i zaczniemy od wymnożenia mianownika przez to samo wyrażenie, które się w nim znajduje, ale z przeciwnym znakiem czyli 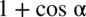 . Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie.
. Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie.
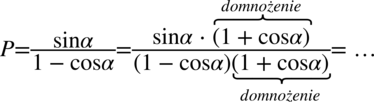
Po wymnożeniu mianownika okaże się, że otrzymujemy przekształcenie jedynki trygonometrycznej, co znacznie ułatwi sprawę. Nawiasy w mianowniku różnią się znakiem pośrodku, także skorzystam ze wzoru skróconego mnożenia 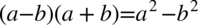 (wynik będzie identyczny jeśli zdecydujemy się na „zwyczajne” wymnożenie nawiasów, ale jest to sposób bardziej pracochłonny):
(wynik będzie identyczny jeśli zdecydujemy się na „zwyczajne” wymnożenie nawiasów, ale jest to sposób bardziej pracochłonny):
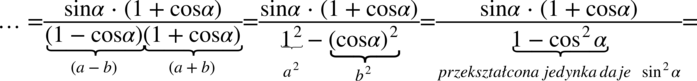
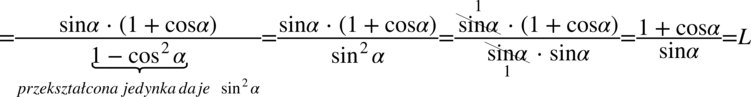

Jak widać w liczniku nie pozbywaliśmy się nawiasów. Był to specjalny zabieg w celu skrócenia sinusa z licznika z sinusem z mianownika. Jeżeli zbyt wcześnie pozbylibyśmy się nawiasów w liczniku nie zauważylibyśmy możliwości późniejszego skracania.
II sposób
Tym razem będziemy przekształcać lewą stronę i zaczniemy od wymnożenia mianownika przez sinus w celu otrzymania sinusa do kwadratu, a co za tym idzie da to nam możliwość skorzystania z przekształconej jedynki trygonometrycznej, bo 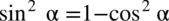 . Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie, także licznik również zostanie wymnożony przez sinus.
. Oczywiście jeżeli wymnaża się mianownik, to obowiązkowo trzeba to samo zrobić z licznikiem aby wartość wyrażenia nie uległa zmianie, także licznik również zostanie wymnożony przez sinus.
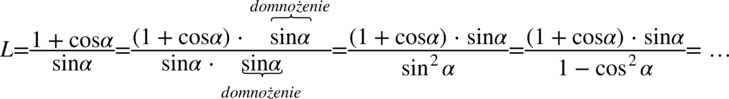
Kolejny etap stanowi rozłożenie mianownika ze wzoru skróconego mnożenia
 , ponieważ wyrażenie z mianownika
, ponieważ wyrażenie z mianownika
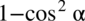 można rozpisać
można rozpisać
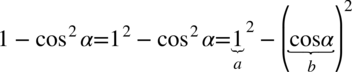 i wyłowić
i wyłowić
 oraz
oraz
 :
:

Dodawanie jest zamknięte w nawiasach, zatem można skrócić identyczne nawiasy z licznika i mianownika:
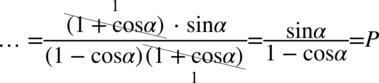

Jak widać licznik nie był celowo wymnażany w celu skrócenia go z identycznym nawiasem z mianownika.
Przykład 35
[kliknij aby rozwinąć] 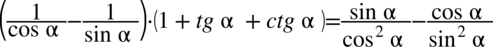
Założenie: 
(żaden z mianowników nie może być równy  ). Sinus i cosinus podniesiony do kwadratu nie może być równy 0, to także sam sinus i cosinus nie może być równy 0, bo zero do kwadratu to nadal zero. Także założenie można zapisać krócej
). Sinus i cosinus podniesiony do kwadratu nie może być równy 0, to także sam sinus i cosinus nie może być równy 0, bo zero do kwadratu to nadal zero. Także założenie można zapisać krócej  .
.
Lewa strona równości jest dłuższa zatem to ją będziemy przekształcać. Występują tu nawiasy, dlatego na początku pozbędziemy się ich wymnażając poszczególne składniki:
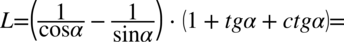
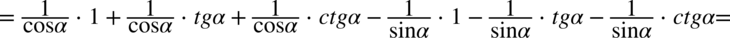
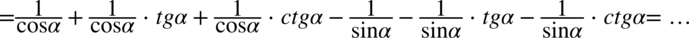
Następnym krokiem będzie zamiana tangensa i cotangensa zgodnie ze wzorami 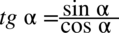 oraz
oraz 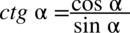 , bo po prawej stronie tożsamości występują tylko sinusy i cosinusy:
, bo po prawej stronie tożsamości występują tylko sinusy i cosinusy:
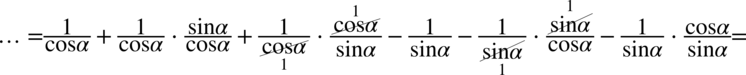


Przykład 36
[kliknij aby rozwinąć] 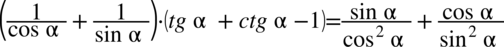
Założenie: 
(żaden z mianowników nie może być równy  ). Sinus i cosinus podniesiony do kwadratu nie może być równy 0, to także sam sinus i cosinus nie może być równy 0, bo zero do kwadratu to nadal zero. Także założenie można zapisać krócej
). Sinus i cosinus podniesiony do kwadratu nie może być równy 0, to także sam sinus i cosinus nie może być równy 0, bo zero do kwadratu to nadal zero. Także założenie można zapisać krócej  .
.
Lewa strona równości jest dłuższa zatem to ją będziemy przekształcać. Występują tu nawiasy, dlatego na początku pozbędziemy się ich wymnażając poszczególne składniki.
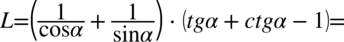
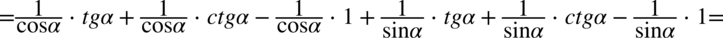
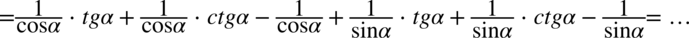
Następnym krokiem będzie zamiana tangensa i cotangensa zgodnie ze wzorami 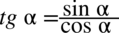 oraz
oraz 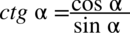 , bo po prawej stronie tożsamości występują tylko sinusy i cosinusy:
, bo po prawej stronie tożsamości występują tylko sinusy i cosinusy: