
Przykład 25
[kliknij aby rozwinąć] 
Założenie: 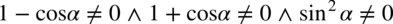 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  )
)
Po przekształceniu 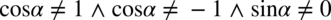 (jeżeli sinus podniesiony do kwadratu nie może być równy
(jeżeli sinus podniesiony do kwadratu nie może być równy  , to także sam sinus nie może być równy
, to także sam sinus nie może być równy  , bo zero do kwadratu to nadal zero).
, bo zero do kwadratu to nadal zero).
Zdecydowanie lewa strona równania jest dłuższa, znajdują się tu dwie kreski ułamkowe, po prawej stronie mamy jedną kreskę ułamkową, dlatego logiczne jest znalezienie wspólnego mianownika po lewej stronie w celu stworzenia właśnie jednej kreski ułamkowej:
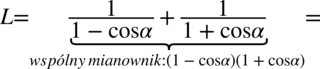

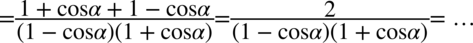
Nie występuje tu możliwość skracania, zatem pozostaje nam wymnożenie nawiasów z mianownika. Warto się wstrzymywać z wymnażaniem mianownika do samego końca, ponieważ można stracić z oczu ewentualność skracania, a przecież wymnożenia można wykonać później. Zauważmy, że nawiasy różnią się jedynie znakiem, także można skorzystać ze wzoru skróconego mnożenia 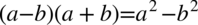 lub wymnożyć „na piechotę” (i tak otrzymamy ten sam wynik):
lub wymnożyć „na piechotę” (i tak otrzymamy ten sam wynik):
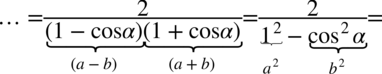


Przykład 26
[kliknij aby rozwinąć] 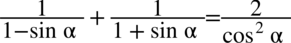
Założenie:  (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  )
)
Po przekształceniu 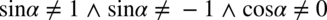 (jeżeli cosinus podniesiony do kwadratu nie może być równy
(jeżeli cosinus podniesiony do kwadratu nie może być równy  , to także sam cosinus nie może być równy
, to także sam cosinus nie może być równy  , bo zero do kwadratu to nadal zero)
, bo zero do kwadratu to nadal zero)
Zdecydowanie lewa strona równości jest dłuższa, znajdują się tu dwie kreski ułamkowe, po prawej stronie mamy jedną kreskę ułamkową, dlatego logiczne jest znalezienie wspólnego mianownika po lewej stronie w celu stworzenia właśnie jednej kreski ułamkowej.

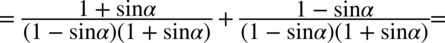

Nie występuje tu możliwość skracania, zatem pozostaje nam wymnożenie nawiasów z mianownika. Warto się wstrzymywać z wymnażaniem mianownika do samego końca, ponieważ można stracić z oczu ewentualność skracania, a przecież wymnożenia można wykonać później. Zauważmy, że nawiasy różnią się jedynie znakiem, także można skorzystać ze wzoru skróconego mnożenia 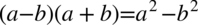 lub wymnożyć „na piechotę” (i tak otrzymamy ten sam wynik):
lub wymnożyć „na piechotę” (i tak otrzymamy ten sam wynik):
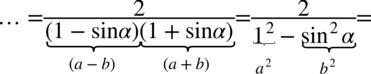


Przykład 27
[kliknij aby rozwinąć] 
Założenie: 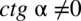 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Od razu przestrzegam przed skracaniem w stylu  . Nie wolno tego robić, ponieważ w liczniku występuje odejmowanie. Aby skracanie było możliwe znak odejmowania wraz z otaczającymi go składnikami musi być zamknięte w nawiasie:
. Nie wolno tego robić, ponieważ w liczniku występuje odejmowanie. Aby skracanie było możliwe znak odejmowania wraz z otaczającymi go składnikami musi być zamknięte w nawiasie: 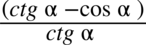 . Jak widać po wprowadzeniu nawiasu nie ma jak dokonać skracania. Pamiętajmy, że elementy z wnętrza nawiasu są nietykalne przy skracaniu!
. Jak widać po wprowadzeniu nawiasu nie ma jak dokonać skracania. Pamiętajmy, że elementy z wnętrza nawiasu są nietykalne przy skracaniu!
Prawa strona równania jest dłuższa, poza tym występuje tu cotangens, po lewej stronie go nie ma, więc pozbędziemy się go stosując wzór 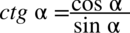 . Ponadto po prawej stronie znajduje się kreska ułamkowa, pozbędziemy się jej rozkładając wyrażenie na prostsze ułamki jak na ułamkach zwykłych:
. Ponadto po prawej stronie znajduje się kreska ułamkowa, pozbędziemy się jej rozkładając wyrażenie na prostsze ułamki jak na ułamkach zwykłych: 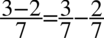 . Jaka będzie kolejność czynności (zamiana cotangensa lub pozbycie się kreski ułamkowej) to już zależy od Was, ale najlepiej zawsze się zastanowić, która droga będzie najkrótsza.
. Jaka będzie kolejność czynności (zamiana cotangensa lub pozbycie się kreski ułamkowej) to już zależy od Was, ale najlepiej zawsze się zastanowić, która droga będzie najkrótsza.
I sposób
Zacznę od rozbicia prawej strony na dwa prostsze ułamki 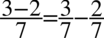 .
.
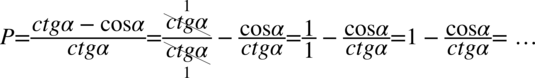
Teraz dokonam zamiany cotangensa na sinus i cosinus stosując wzór 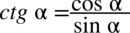 , ponieważ po lewej stronie nie występuje cotangens:
, ponieważ po lewej stronie nie występuje cotangens:

Teraz pozbędę się piętrowego ułamka zamieniając główną kreskę ułamkową na znak dzielenia. Dla ułatwienia obliczeń zastosowano 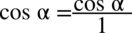 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie).
nie ulega zmianie).
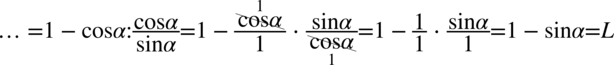

II sposób
Zacznę od zamiany cotangensa na sinus i cosinus korzystając ze wzoru 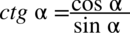 , ponieważ cotangens po lewej stronie nie występuje:
, ponieważ cotangens po lewej stronie nie występuje:
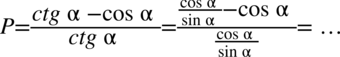
Kolejny etap to sprowadzenie do wspólnego mianownika licznika powstałego ułamka. W tym celu zostanie zastosowany zapis 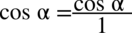 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
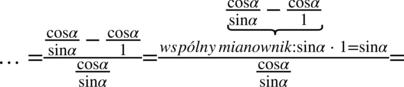
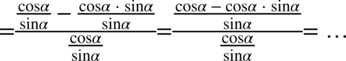
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i następnie mnożąc przez odwrotność:
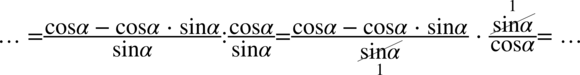
Skrócenie sinusa nie stanowiło problemu, teraz zajmijmy się cosinusem. Najpierw trzeba wyciągnąć cosinus z licznika pierwszego ułamka przed nawias (element powtarzający się), ponieważ jeszcze w tej postaci odejmowanie nie jest zamknięte w nawiasie. Pamiętamy, że przy wyciąganiu przed nawias jeżeli zabieramy „wszystko” to zawsze zostaje  :
:
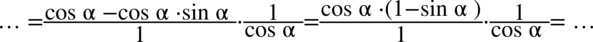
Teraz już można skracać bez obaw:


Przykład 24
[kliknij aby rozwinąć] 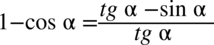
Założenie: 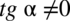 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Od razu przestrzegam przed skracaniem w stylu 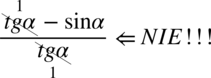 . Nie wolno tego robić, ponieważ w liczniku występuje odejmowanie. Aby skracanie było możliwe znak odejmowania wraz z otaczającymi go składnikami musi być zamknięte w nawiasie:
. Nie wolno tego robić, ponieważ w liczniku występuje odejmowanie. Aby skracanie było możliwe znak odejmowania wraz z otaczającymi go składnikami musi być zamknięte w nawiasie: 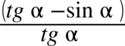 . Jak widać po wprowadzeniu nawiasu nie ma jak dokonać skracania. Pamiętajmy, że elementy z wnętrza nawiasu są nietykalne przy skracaniu!
. Jak widać po wprowadzeniu nawiasu nie ma jak dokonać skracania. Pamiętajmy, że elementy z wnętrza nawiasu są nietykalne przy skracaniu!
Prawa strona równania jest dłuższa, poza tym występuje tu tangens, po lewej stronie go nie ma, więc pozbędziemy się go stosując wzór 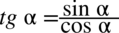 . Ponadto po prawej stronie znajduje się kreska ułamkowa, pozbędziemy się jej rozkładając wyrażenie na prostsze ułamki jak na ułamkach zwykłych:
. Ponadto po prawej stronie znajduje się kreska ułamkowa, pozbędziemy się jej rozkładając wyrażenie na prostsze ułamki jak na ułamkach zwykłych: 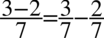 . Jaka będzie kolejność czynności (zamiana tangensa lub pozbycie się kreski ułamkowej) to już zależy od Was, ale najlepiej zawsze się zastanowić, która droga będzie najkrótsza.
. Jaka będzie kolejność czynności (zamiana tangensa lub pozbycie się kreski ułamkowej) to już zależy od Was, ale najlepiej zawsze się zastanowić, która droga będzie najkrótsza.
I sposób
Zacznę od rozbicia prawej strony na dwa prostsze ułamki 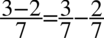 .
.
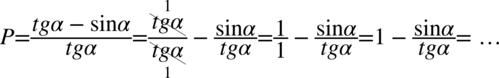
Teraz dokonam zamiany tangensa na sinus i cosinus stosując wzór 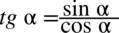 , ponieważ po lewej stronie nie występuje tangens:
, ponieważ po lewej stronie nie występuje tangens:

Teraz pozbędę się piętrowego ułamka zamieniając główną kreskę ułamkową na znak dzielenia. Dla ułatwienia obliczeń zastosowano 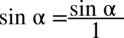 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie).
nie ulega zmianie).
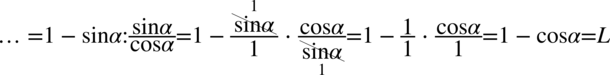

II sposób
Zacznę od zamiany tangensa na sinus i cosinus korzystając ze wzoru 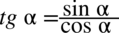 , ponieważ tangens po lewej stronie nie występuje:
, ponieważ tangens po lewej stronie nie występuje:

Kolejny etap to sprowadzenie do wspólnego mianownika licznika powstałego ułamka. W tym celu zostanie zastosowany zapis 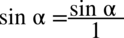 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
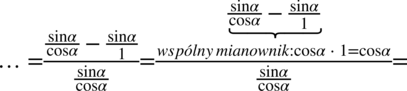
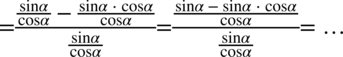
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i następnie mnożąc przez odwrotność:
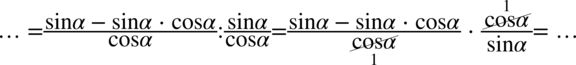
Skrócenie cosinusa nie stanowiło problemu, teraz zajmijmy się sinusem. Najpierw trzeba wyciągnąć sinus z licznika pierwszego ułamka przed nawias (element powtarzający się), ponieważ jeszcze w tej postaci odejmowanie nie jest zamknięte w nawiasie. Pamiętamy, że przy wyciąganiu przed nawias jeżeli zabieramy „wszystko” to zawsze zostaje  :
:
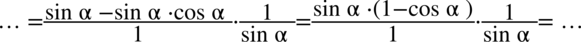
Teraz już można skracać bez obaw:

