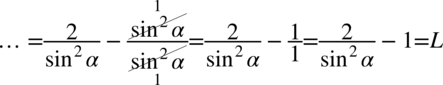Przykład 21
[kliknij aby rozwinąć] 
Założenie: 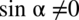 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Lewa strona równości jest zdecydowanie dłuższa. Na początku pozbędziemy się nawiasów wymnażając odpowiednie składniki.
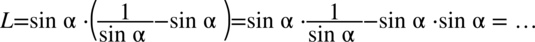
Dla ułatwienia działań na ułamkach zastosujemy zapis 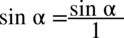 :
:
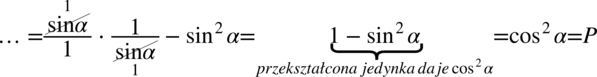

Przykład 22
[kliknij aby rozwinąć] 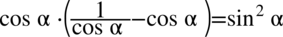
Założenie: 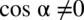 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Lewa strona równości jest zdecydowanie dłuższa. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
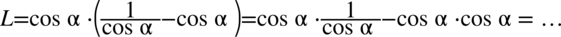
Dla ułatwienia działań na ułamkach zastosujemy zapis 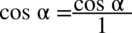 :
:


Przykład 23
[kliknij aby rozwinąć] 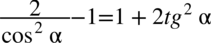
Założenie:  (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  , jeżeli cosinus podniesiony do kwadratu nie może być równy
, jeżeli cosinus podniesiony do kwadratu nie może być równy  , to także sam cosinus nie może być równy
, to także sam cosinus nie może być równy  , bo zero do kwadratu to nadal zero)
, bo zero do kwadratu to nadal zero)
Zaczniemy od prawej strony, ponieważ występuje tu tangens, a po lewej stronie go nie ma, więc pozbędziemy się go korzystając ze wzoru 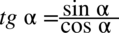 , dzięki czemu stworzy się też kreska ułamkowa, która występuje po lewej stronie. Oczywiście można próbować zaczynać przekształcanie od lewej strony, ale tak jak już wcześniej wspomniałam rozkładanie liczb na przykład z jedynki trygonometrycznej raczej należy zostawiać na sam koniec, chyba, że nie ma innego wyjścia.
, dzięki czemu stworzy się też kreska ułamkowa, która występuje po lewej stronie. Oczywiście można próbować zaczynać przekształcanie od lewej strony, ale tak jak już wcześniej wspomniałam rozkładanie liczb na przykład z jedynki trygonometrycznej raczej należy zostawiać na sam koniec, chyba, że nie ma innego wyjścia.
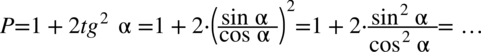
Aby uzyskać pewność jak mnożyć np.  i wykonywać inne działania na ułamkach stosujemy zapis
i wykonywać inne działania na ułamkach stosujemy zapis  oraz
oraz  :
:

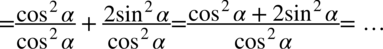
Na tym etapie pozbędziemy się wszelkich sinusów zamieniając je na cosinusy, ponieważ po lewej stronie są wyłącznie cosinusy, a właśnie do ich uzyskania dążymy:
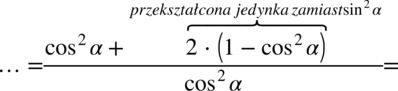
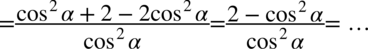
Zauważmy, że po lewej stronie jest kreska ułamkowa, ale obok niej występuje  ,aby ją uzyskać zastosujemy rozdzielenie ułamków tak jak można to zrobić na prostszych liczbach
,aby ją uzyskać zastosujemy rozdzielenie ułamków tak jak można to zrobić na prostszych liczbach 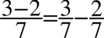 :
:
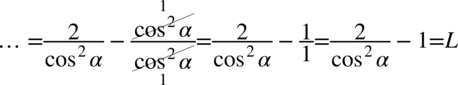

Przykład 24
[kliknij aby rozwinąć] 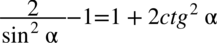
Założenie:  (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  , jeżeli sinus podniesiony do kwadratu nie może być równy
, jeżeli sinus podniesiony do kwadratu nie może być równy  , to także sam sinus nie może być równy
, to także sam sinus nie może być równy  , bo zero do kwadratu to nadal zero)
, bo zero do kwadratu to nadal zero)
Zaczniemy od prawej strony, ponieważ występuje tu cotangens, a po lewej stronie go nie ma, więc pozbędziemy się go korzystając ze wzoru 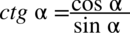 , dzięki czemu stworzy się też kreska ułamkowa, która występuje po lewej stronie. Oczywiście można próbować zaczynać przekształcanie od lewej strony, ale tak jak już wcześniej wspomniałam rozkładanie liczb na przykład z jedynki trygonometrycznej raczej należy zostawiać na sam koniec, chyba, że nie ma innego wyjścia.
, dzięki czemu stworzy się też kreska ułamkowa, która występuje po lewej stronie. Oczywiście można próbować zaczynać przekształcanie od lewej strony, ale tak jak już wcześniej wspomniałam rozkładanie liczb na przykład z jedynki trygonometrycznej raczej należy zostawiać na sam koniec, chyba, że nie ma innego wyjścia.

Aby uzyskać pewność jak mnożyć np.  i wykonywać inne działania na ułamkach stosujemy zapis
i wykonywać inne działania na ułamkach stosujemy zapis  oraz
oraz  :
:


Na tym etapie pozbędziemy się wszelkich cosinusów zamieniając je na sinusy, ponieważ po lewej stronie są wyłącznie sinusy, a właśnie do ich uzyskania dążymy:

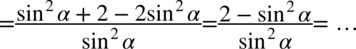
Zauważmy, że po lewej stronie jest kreska ułamkowa, ale obok niej występuje  ,aby ją uzyskać zastosujemy rozdzielenie ułamków tak jak można to zrobić na prostszych liczbach
,aby ją uzyskać zastosujemy rozdzielenie ułamków tak jak można to zrobić na prostszych liczbach 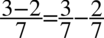 :
: