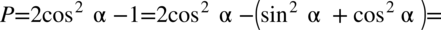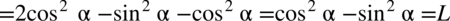Przykład 17
[kliknij aby rozwinąć] 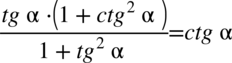
Założenie: 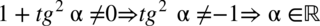
(cały mianownik nie może być równy  , bo nie dzieli się przez
, bo nie dzieli się przez  , ale po przekształceniu założenia otrzymujemy tangens podniesiony do kwadratu różny od
, ale po przekształceniu założenia otrzymujemy tangens podniesiony do kwadratu różny od  , jak wiadomo jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej, zatem okazuje się, że nie ma ograniczeń co do wartości tangensa kąta
, jak wiadomo jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej, zatem okazuje się, że nie ma ograniczeń co do wartości tangensa kąta 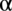 i co za tym idzie samego kąta)
i co za tym idzie samego kąta)
Tu też ostrzegam przed nieprawidłowym skracaniem, o ile licznik ułamka jest w idealnej formie do skracania (pamiętajmy, że nie można skracać pojedynczych elementów z wnętrza nawiasu, cały nawias tak, ale musi być on identyczny jak cały mianownik), to gdyby komuś przyszło do głowy skracanie typu 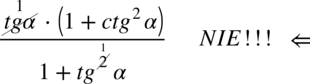 to jest to niedozwolone, ponieważ dodawanie wraz z okalającymi elementami w mianowniku musi być zamknięte w nawiasie. Po zamknięciu w nawiasie
to jest to niedozwolone, ponieważ dodawanie wraz z okalającymi elementami w mianowniku musi być zamknięte w nawiasie. Po zamknięciu w nawiasie 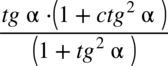 nie ma już z czym skrócić tangensa z licznika.
nie ma już z czym skrócić tangensa z licznika.
Lewa strona równania jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Na początku warto pozbyć się nawiasu w liczniku wymnażając kolejno składniki:
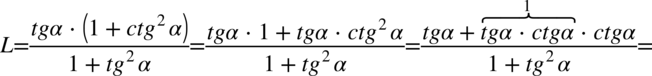
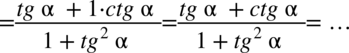
Zauważmy, że w przykładzie występują same tangensy i cotangensy, a po prawej stronie mamy otrzymać cotangens, zatem kolejnym krokiem po pozbyciu się nawiasów będzie zamiana tangensów na cotangensy zgodnie ze wzorem 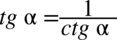 oraz sprowadzenie powstałych ułamków z licznika i mianownika mega ułamka do wspólnego mianownika, dla ułatwienia działań zastosujemy zapis
oraz sprowadzenie powstałych ułamków z licznika i mianownika mega ułamka do wspólnego mianownika, dla ułatwienia działań zastosujemy zapis 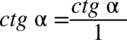 oraz
oraz  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
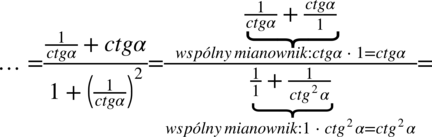

Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i postępując dokładnie tak jak na ułamkach zwykłych:

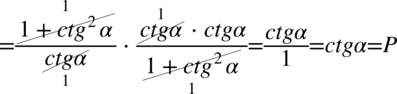

Przykład 18
[kliknij aby rozwinąć] 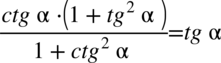
Założenie: 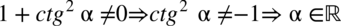
(cały mianownik nie może być równy  , bo nie dzieli się przez
, bo nie dzieli się przez  , ale po przekształceniu założenia otrzymujemy cotangens podniesiony do kwadratu różny od
, ale po przekształceniu założenia otrzymujemy cotangens podniesiony do kwadratu różny od  , jak wiadomo jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej, zatem okazuje się, że nie ma ograniczeń co do wartości cotangensa kąta
, jak wiadomo jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej, zatem okazuje się, że nie ma ograniczeń co do wartości cotangensa kąta 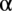 i co za tym idzie samego kąta)
i co za tym idzie samego kąta)
Tu też ostrzegam przed nieprawidłowym skracaniem, o ile licznik ułamka jest w idealnej formie do skracania (pamiętajmy, że nie można skracać pojedynczych elementów z wnętrza nawiasu, cały nawias tak, ale musi być on identyczny jak cały mianownik), to gdyby komuś przyszło do głowy skracanie typu 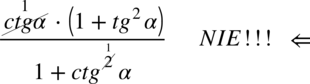 to jest to niedozwolone, ponieważ dodawanie wraz z okalającymi elementami w mianowniku musi być zamknięte w nawiasie. Po zamknięciu w nawiasie
to jest to niedozwolone, ponieważ dodawanie wraz z okalającymi elementami w mianowniku musi być zamknięte w nawiasie. Po zamknięciu w nawiasie 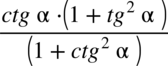 nie ma już z czym skrócić cotangensa z licznika.
nie ma już z czym skrócić cotangensa z licznika.
Lewa strona równania jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Na początku warto pozbyć się nawiasu w liczniku wymnażając kolejno składniki:
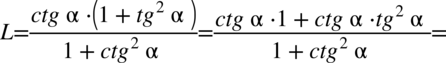
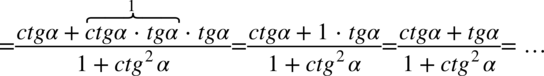
Zauważmy, że w przykładzie występują same tangensy i cotangensy, a po prawej stronie mamy otrzymać tangens, zatem kolejnym krokiem po pozbyciu się nawiasów będzie zamiana cotangensów na tangensy zgodnie ze wzorem 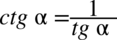 oraz sprowadzenie powstałych ułamków z licznika i mianownika mega ułamka do wspólnego mianownika, dla ułatwienia działań zastosujemy zapis
oraz sprowadzenie powstałych ułamków z licznika i mianownika mega ułamka do wspólnego mianownika, dla ułatwienia działań zastosujemy zapis 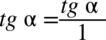 oraz
oraz  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
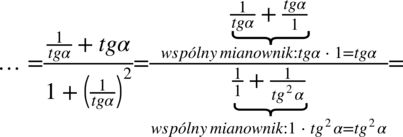
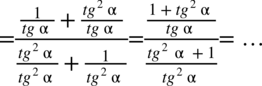
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i postępując dokładnie tak jak na ułamkach zwykłych:

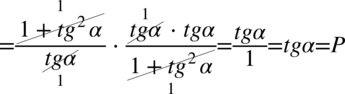

Przykład 19
[kliknij aby rozwinąć] 
Równość można sprawdzić na kilka sposobów. Obie strony są identyczne względem długości.
Można rozłożyć liczbę  zgodnie ze wzorem
zgodnie ze wzorem 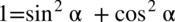 . Oczywiście jest to jak najbardziej prawidłowe rozwiązanie, ale najlepiej w ostateczności korzystać z rozkładania
. Oczywiście jest to jak najbardziej prawidłowe rozwiązanie, ale najlepiej w ostateczności korzystać z rozkładania  na sinus i cosinus, ponieważ przykład może się rozrosnąć do niebotycznych rozmiarów i nie będzie wiadomo co z tym później zrobić - zwłaszcza w skomplikowanych tożsamościach. Zresztą później i tak trzeba będzie korzystać z przekształceń jedynki trygonometrycznej i przykład niepotrzebnie się wydłuży, zwłaszcza że mamy
na sinus i cosinus, ponieważ przykład może się rozrosnąć do niebotycznych rozmiarów i nie będzie wiadomo co z tym później zrobić - zwłaszcza w skomplikowanych tożsamościach. Zresztą później i tak trzeba będzie korzystać z przekształceń jedynki trygonometrycznej i przykład niepotrzebnie się wydłuży, zwłaszcza że mamy  po obu stronach i nie warto się jej pozbywać.
po obu stronach i nie warto się jej pozbywać.
I sposób
Zaczniemy od lewej strony, po prawej stronie mamy otrzymać cosinus, a jeżeli jest to cosinus do kwadratu, dlatego na pewno skorzystamy z przekształconej jedynki trygonometrycznej aby pozbyć się sinusa: 
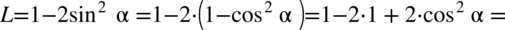
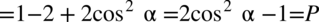

II sposób
Zaczniemy od prawej strony, po lewej stronie mamy otrzymać sinus, a jeżeli jest to cosinus do kwadratu, dlatego na pewno skorzystamy z przekształconej jedynki trygonometrycznej aby pozbyć się cosinusa:

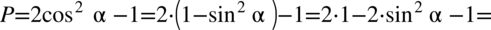
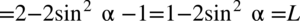

Przykład 20
[kliknij aby rozwinąć] 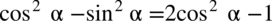
Obie strony równości są podobnej długości, zatem nie ważne od której strony zaczniemy przekształcenia.
I sposób
Zaczniemy od lewej strony, po prawej mamy otrzymać cosinus do kwadratu, dlatego od razu nasuwa się na myśl wykorzystanie przekształconej jedynki trygonometrycznej aby pozbyć się sinusa po lewej stronie  :
:
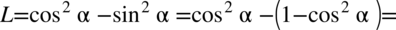
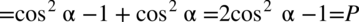

II sposób
Zaczniemy od prawej strony. Tak jak już wcześniej wspomniano zdecydowanie lepiej jest rozkładać  ze wzoru
ze wzoru 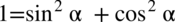 w ostateczności, ale po lewej stronie nie występuje
w ostateczności, ale po lewej stronie nie występuje  , zatem można zastosować ten wzór aby się jej pozbyć.
, zatem można zastosować ten wzór aby się jej pozbyć.