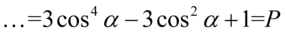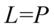Przykład 145
[kliknij aby rozwinąć] 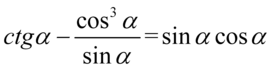
Założenie: 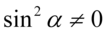 (mianownik nie może być równy
(mianownik nie może być równy  ).
).
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Zaczniemy od zlikwidowania cotangensa, ponieważ po prawej stronie do której uzyskania dążymy cotangensy nie występują. Korzystamy ze wzoru 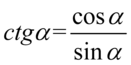 :
:
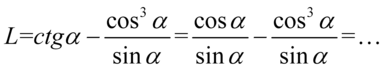
Kolejny etap to zapisanie wszystkiego na jednej kresce ułamkowej. W tym przypadku mamy komfortową sytuację, ponieważ obydwa ułamki mają wspólny mianownik:
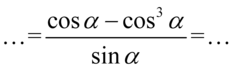
Teraz musimy wyciągnąć w liczniku 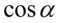 przed nawias, ponieważ nic innego nie można tu wykonać, pamiętajmy, że zabierając wszystko w nawiasie zostaje jedynka:
przed nawias, ponieważ nic innego nie można tu wykonać, pamiętajmy, że zabierając wszystko w nawiasie zostaje jedynka:
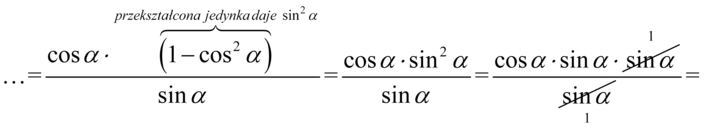
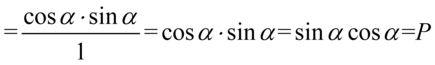
Skracanie było możliwe, ponieważ w ułamku występowało tylko mnożenie, na końcu zmieniliśmy kolejność składników, bo w mnożeniu mamy do czynienia z przemiennością czyli  .
.
Przykład 146
[kliknij aby rozwinąć] 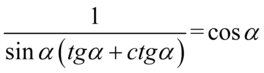
Założenie: 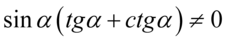 (mianownik nie może być równy
(mianownik nie może być równy  ). Po rozdzieleniu mnożenia mamy
). Po rozdzieleniu mnożenia mamy  , ponieważ iloczyn dwóch składników jest różny od zera tylko wtedy, gdy każdy z czynników osobno jest różny od zera. Ostatecznie otrzymujemy:
, ponieważ iloczyn dwóch składników jest różny od zera tylko wtedy, gdy każdy z czynników osobno jest różny od zera. Ostatecznie otrzymujemy: 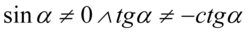 .
.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Zaczniemy od likwidacji nawiasów kolejno wymnażając składniki:
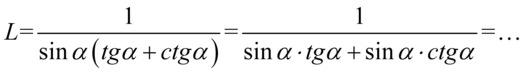
Teraz pozbędziemy się tangensa i cotangensa korzystając ze wzorów 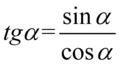 oraz
oraz 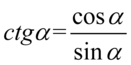 , ponieważ po prawej stronie do której uzyskania dążymy jest tylko cosinus:
, ponieważ po prawej stronie do której uzyskania dążymy jest tylko cosinus:
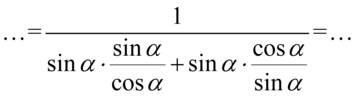
Dla ułatwienia działań zastosujemy zapis 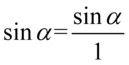 , aby było wiadomo jakie składniki ze sobą wymnażamy:
, aby było wiadomo jakie składniki ze sobą wymnażamy:
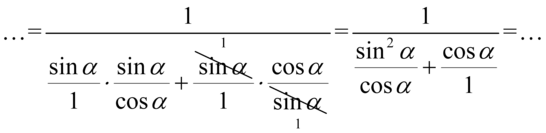
Teraz ułamki z dolnego piętra sprowadzimy do wspólnego mianownika:
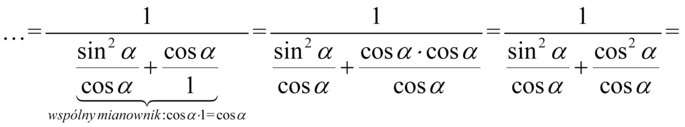
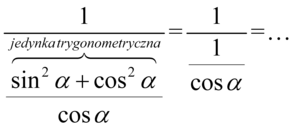
Na końcu pozbędziemy się ułamka piętrowego zamieniając główną kreskę ułamkową na znak dzielenia, a następnie zastępując dzielenie mnożeniem przez odwrotność:
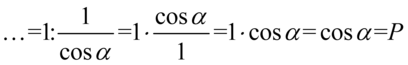
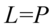
Przykład 147
[kliknij aby rozwinąć] 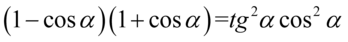
Lewa strona wydaje się dłuższa, ale po prawej mamy tangens, który znacznie łatwiej zamienić na sinus i cosinus niż stworzyć do z jedynek i sinusów. Tak więc pierwszym krokiem będzie likwidacja cotangensa przy użyciu wzoru 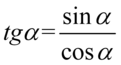 :
:
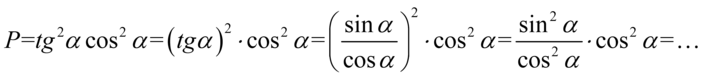
Aby ułatwić dalsze działania zostanie użyty zapis 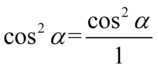 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez 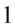 nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:
nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:
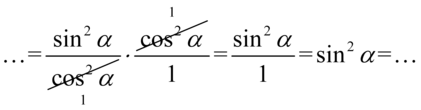
Przyglądając się lewej stronie widzimy tam jedynki i cosinusy, otrzymaliśmy sinus podniesiony do kwadratu, który można z łatwością zamienić na cosinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 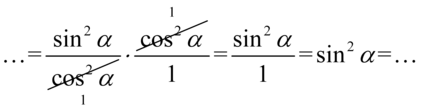 :
:
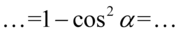
Teraz musimy stworzyć nawiasy. Warto zauważyć, że w wyniku mamy dwa elementy oddzielone minusem, w tym jeden podniesiony do kwadratu, co jest charakterystyczne dla wzoru skróconego mnożenia postaci: 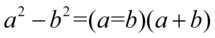 . Aby łatwiej go zauważyć można inaczej zapisać jedynkę
. Aby łatwiej go zauważyć można inaczej zapisać jedynkę  , bo jedynka podniesiona do dowolnej potęgi i tak wynosi
, bo jedynka podniesiona do dowolnej potęgi i tak wynosi 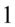 . Jak wyłowić
. Jak wyłowić 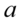 i
i 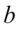 ze wzoru? Należy się zastanowić co trzeba podnieść do kwadratu aby otrzymać te dwa elementy, czyli
ze wzoru? Należy się zastanowić co trzeba podnieść do kwadratu aby otrzymać te dwa elementy, czyli 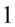 i
i 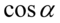 :
:
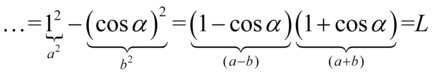
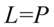
Przykład 148
[kliknij aby rozwinąć] 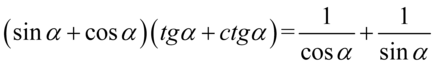
Założenie: 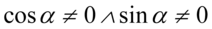 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  )
)
Lewa strona równości jest wyraźnie dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasów kolejno wymnażając składniki:
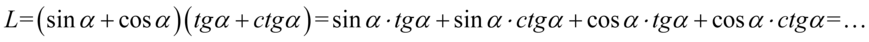
Teraz pozbędziemy się tangensa i cotangensa korzystając ze wzorów 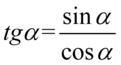 oraz
oraz 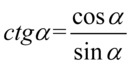 , ponieważ po prawej stronie do której uzyskania dążymy jest tylko cosinus:
, ponieważ po prawej stronie do której uzyskania dążymy jest tylko cosinus:
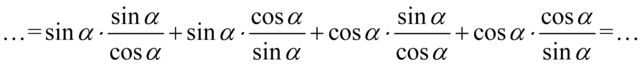
Aby ułatwić dalsze działania zostanie użyty zapis 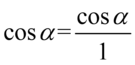 oraz
oraz 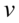 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez 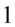 nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:
nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:
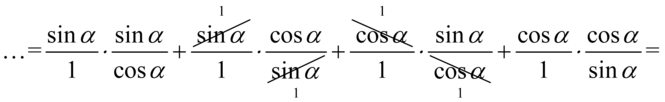
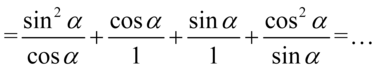
Teraz sprytnie pogrupujemy ułamki w celu sprowadzenia do wspólnego mianownika aby otrzymać żądaną prawą stronę. Dla dwóch pierwszych i dwóch ostatnich znajdziemy wspólny mianownik, ponieważ po prawej stronie jest 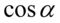 o
o 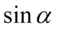 w mianownikach. Wspólny mianownik dla wszystkich ułamków oczywiście nie będzie błędem, ale znacznie wydłuży czas dowodzenia tożsamości:
w mianownikach. Wspólny mianownik dla wszystkich ułamków oczywiście nie będzie błędem, ale znacznie wydłuży czas dowodzenia tożsamości:
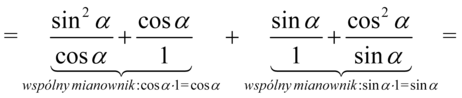
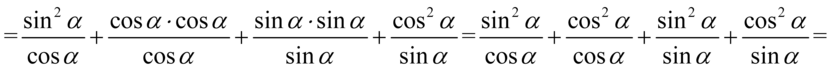
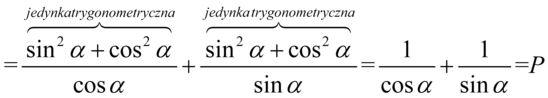
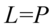
Przykład 149
[kliknij aby rozwinąć] 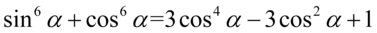
Prawa strona jest dłuższa, ale po lewej stronie mamy większe potęgi, także to ta strona będzie przekształcana. Na początku skorzystamy ze wzoru 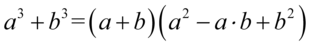 . Aby łatwiej go zauważyć wykonamy kilka wcześniejszych przekształceń korzystając z prawa działań na potęgach:
. Aby łatwiej go zauważyć wykonamy kilka wcześniejszych przekształceń korzystając z prawa działań na potęgach:
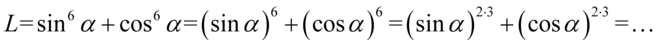
Korzystając ze wzoru 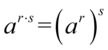 otrzymujemy:
otrzymujemy:
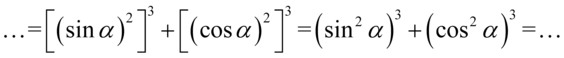
Wreszcie rozpisujemy wzór, gdzie  i
i  :
:
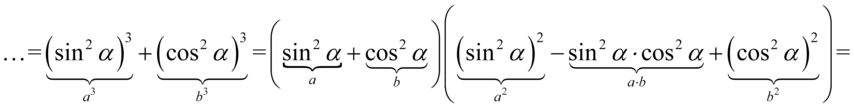
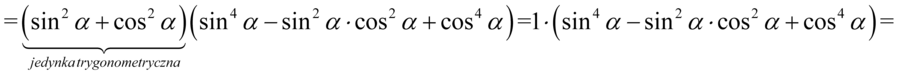
Jeżeli wymnażamy przez  jakiekolwiek wyrażenie to otrzymujemy to samo wyrażenie.
jakiekolwiek wyrażenie to otrzymujemy to samo wyrażenie.
Jak widać powstała już potęga o żądanym wykładniku przy cosinusie, czyli 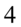 , którą mamy po prawej stronie tożsamości, ale są jeszcze sinusy, których należy się pozbyć. W związku z tym skorzystamy ze wzoru na przekształconą jedynkę trygonometryczną
, którą mamy po prawej stronie tożsamości, ale są jeszcze sinusy, których należy się pozbyć. W związku z tym skorzystamy ze wzoru na przekształconą jedynkę trygonometryczną 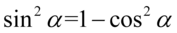 , ale zanim to wykonamy rozpiszemy
, ale zanim to wykonamy rozpiszemy 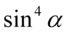 z własności
z własności 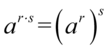 aby uzyskać
aby uzyskać 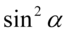 czyli
czyli 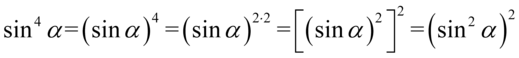 . Wstawiamy do przykładu oczywiście pamiętając o nawiasach aby nie zgubić znaków:
. Wstawiamy do przykładu oczywiście pamiętając o nawiasach aby nie zgubić znaków:
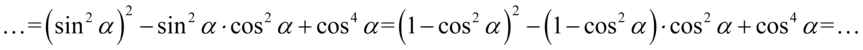
Pierwszy nawias wymaga zastosowania wzoru skróconego mnożenia 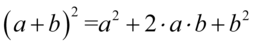 , drugi nawias zniknie po standardowym wymnożeniu składników przez siebie:
, drugi nawias zniknie po standardowym wymnożeniu składników przez siebie:
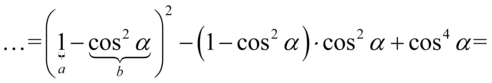
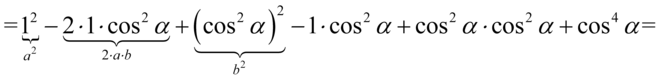
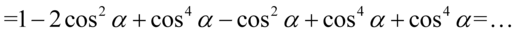
Na koniec dokonujemy redukcji wyrazów podobnych i mamy: