
Przykład 141
[kliknij aby rozwinąć] 
Założenie: 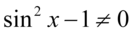 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 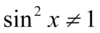 i ostatecznie
i ostatecznie 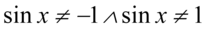 , ponieważ
, ponieważ 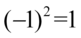 oraz
oraz 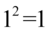 .
.
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Daną tożsamość można udowodnić na dwa sposoby.
I sposób
Licznik i mianownik ułamka przypominają przekształcenia jedynki trygonometrycznej tzn. 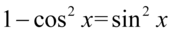 oraz
oraz 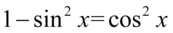 , ale poszczególne składniki są w innej kolejności. Zmieńmy więc tą kolejność, pamiętając przy tym, że wraz z liczbą przenosi się znak stojący przed nią:
, ale poszczególne składniki są w innej kolejności. Zmieńmy więc tą kolejność, pamiętając przy tym, że wraz z liczbą przenosi się znak stojący przed nią:
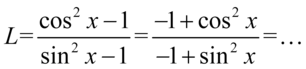
W przekształceniach jedynki trygonometrycznej występują przeciwne znaki, tak więc aby uzyskać pożądane znaki należy wyciągnąć minus przed nawias, który zmieni je na właściwe:
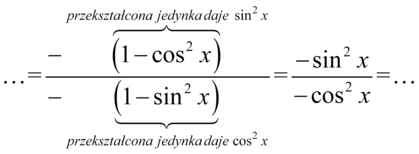
Podczas dzielenia minusy się skrócą, bo 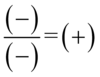 :
:
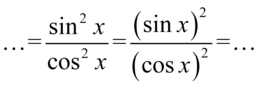
Korzystając z własności 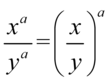 i wzoru
i wzoru 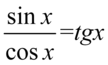 otrzymujemy:
otrzymujemy:
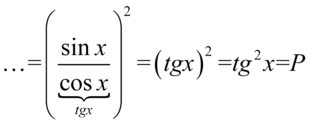
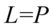
II sposób
Tym razem rozpiszemy jedynkę korzystając z zapisu 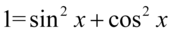 . Należy jednak pamiętać, że w dłuższych przykładach nie warto tego robić, ponieważ dość krótkie wyrażenie może rozrosnąć się do ogromnych rozmiarów. Starajmy się zatem zwijać do jedynki, a nie rozpisywać na sinus i cosinus. W tym przypadku przykład nie jest mocno skomplikowany, także nie utrudnimy sobie obliczeń. Pamiętajmy o nawiasach aby nie pogubić znaków:
. Należy jednak pamiętać, że w dłuższych przykładach nie warto tego robić, ponieważ dość krótkie wyrażenie może rozrosnąć się do ogromnych rozmiarów. Starajmy się zatem zwijać do jedynki, a nie rozpisywać na sinus i cosinus. W tym przypadku przykład nie jest mocno skomplikowany, także nie utrudnimy sobie obliczeń. Pamiętajmy o nawiasach aby nie pogubić znaków:
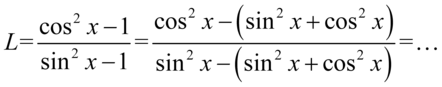
Teraz pozbędziemy się nawiasów, przed obydwoma stoi minus, także opuszczając nawiasy zmienimy znaki na przeciwne:
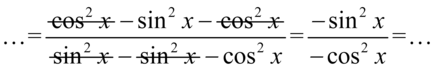
Podczas dzielenia minusy się skrócą, bo 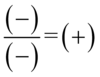 :
:
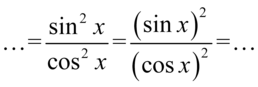
Korzystając z własności 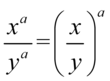 i wzoru
i wzoru 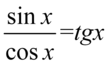 otrzymujemy:
otrzymujemy:
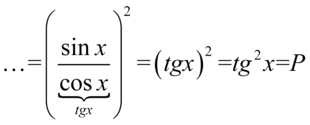
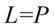
Przykład 142
[kliknij aby rozwinąć] 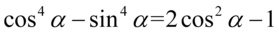
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:

Teraz skorzystamy z własności potęg, gdzie 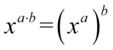 :
:
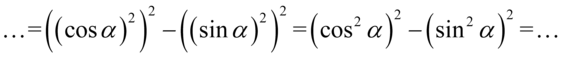
Teraz przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 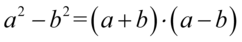 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
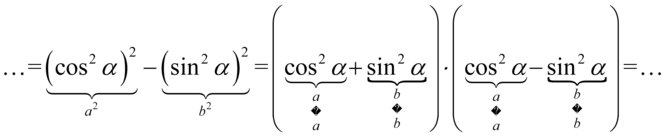
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
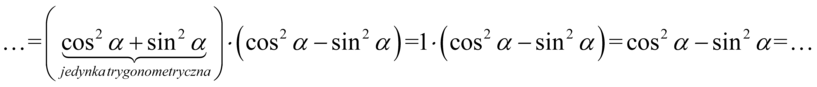
I w końcu ostatnie przekształcenie, które będzie polegało na zlikwidowaniu sinusa, ponieważ po prawej stronie równości sinus nie występuje. W przykładzie mamy sinus do kwadratu, także można go ławo zamienić na cosinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 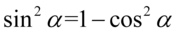 . Pamiętajmy o używaniu nawiasów aby nie pogubić znaków:
. Pamiętajmy o używaniu nawiasów aby nie pogubić znaków:
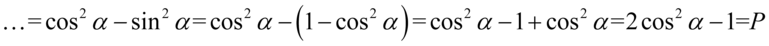

Przykład 143
[kliknij aby rozwinąć] 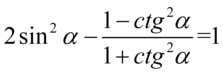
Założenie: 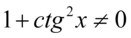 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 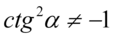 - co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać
- co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać 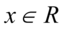 , bo niezależnie od wartości kąta cotangens podniesiony do kwadratu nie będzie ujemny.
, bo niezależnie od wartości kąta cotangens podniesiony do kwadratu nie będzie ujemny.
Znów uprzedzam przed „radosnym” skracaniem w stylu: 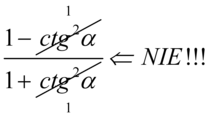 . Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie:
. Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie: 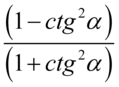 . Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
. Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
Lewa strona tożsamości jest dłuższa i to ona będzie podlegać przekształceniom. Na początku pozbędziemy się cotangensów korzystając ze wzoru 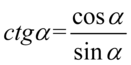 , ponieważ po lewej stronie do której uzyskania dążymy cotangensy nie występują, poza tym łatwiej będzie wykonywać przekształcenia z sinusem znajdującym się na początku przykładu:
, ponieważ po lewej stronie do której uzyskania dążymy cotangensy nie występują, poza tym łatwiej będzie wykonywać przekształcenia z sinusem znajdującym się na początku przykładu:
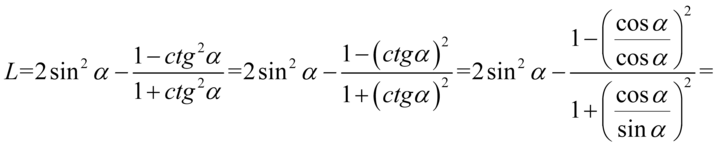
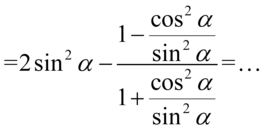
Teraz do powstałych ułamków „wrzucimy” jedynki sprowadzając je do wspólnego mianownika, dla ułatwienia działań użyjemy zapisu 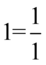 (każda liczba podzielona przez
(każda liczba podzielona przez 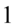 nie ulega zmianie):
nie ulega zmianie):
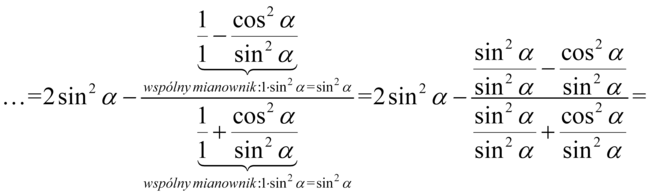
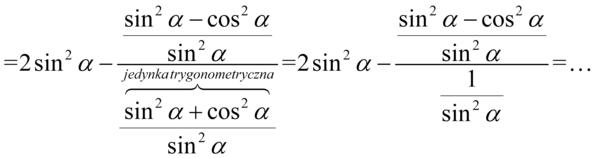
Kolejnym krokiem będzie zlikwidowanie piętrowego ułamka poprzez zamianę kreski ułamkowej na znak dzielenia, a następnie zamiana dzielenia na mnożenie przez odwrotność dzielnika:
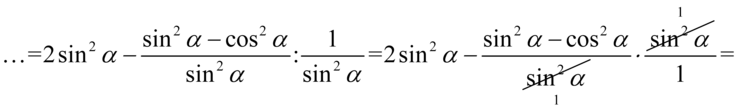
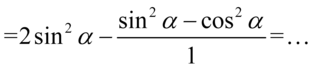
Jedynkę z mianownika można już sobie darować, ale opuszczając ją zapiszemy wyrażenie z licznika w nawiasie, ponieważ jeżeli przed ułamkiem występuje minus, to zmieni on wszystkie znaki w liczniku lub mianowniku:
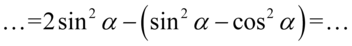
Opuszczamy nawiasy i redukujemy wyrazy podobne. Oczywiście zmieniamy znaki w nawiasie, bo stoi przed nim minus:
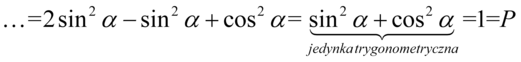
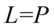
Przykład 143
[kliknij aby rozwinąć] 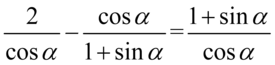
Założenie: 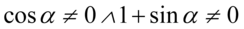 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). W przykładzie mamy dwa identyczne mianowniki, ale nie ma sensu pisać kilka razy tego samego, dlatego w założeniu
). W przykładzie mamy dwa identyczne mianowniki, ale nie ma sensu pisać kilka razy tego samego, dlatego w założeniu 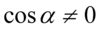 występuje tylko raz. Po przekształceniu otrzymujemy ostatecznie
występuje tylko raz. Po przekształceniu otrzymujemy ostatecznie 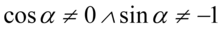 .
.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Po tej stronie mamy dwa ułamki, a po prawej do której uzyskania dążymy mamy jeden ułamek, tak więc najbardziej oczywistą operacją jest sprowadzenie danych ułamków do wspólnego mianownika:
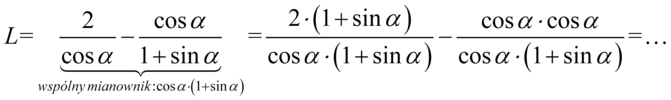
Na początku wymnóżmy wyrażenia w licznikach, na razie zostawmy nawiasy w mianowniku w spokoju, ponieważ może się zdarzyć, że po kilku przekształceniach pojawi się możliwość skracania, a jeśli wymnożymy nawiasy za wcześnie to niekoniecznie ją zauważymy.
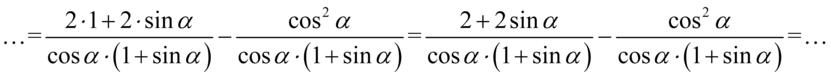
Mamy już wspólny mianownik, tak więc można zapisać wszystko na jednej kresce ułamkowej:
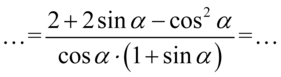
W liczniku niestety nie powstało nic nadzwyczajnego, dlatego przyjrzyjmy się prawej stronie tożsamości, gdzie w liczniku mamy tylko  , także jest tu wskazówka co należy zrobić z licznikiem – pozbędziemy się cosinusa, bo po prawej stronie tożsamości nie ma cosinusa w liczniku. Skorzystamy ze wzoru
, także jest tu wskazówka co należy zrobić z licznikiem – pozbędziemy się cosinusa, bo po prawej stronie tożsamości nie ma cosinusa w liczniku. Skorzystamy ze wzoru  . Nie zapominajmy o nawiasach, bo pogubimy znaki:
. Nie zapominajmy o nawiasach, bo pogubimy znaki:
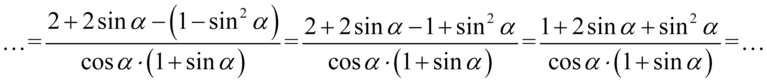
Teraz najtrudniejsza część, w liczniku powstał rozpisany wzór skróconego mnożenia 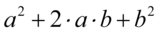 , który należy zwinąć do postaci
, który należy zwinąć do postaci 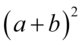 . Aby łatwiej go zauważyć przedstawię rozpisanie. Pamiętajmy, że
. Aby łatwiej go zauważyć przedstawię rozpisanie. Pamiętajmy, że 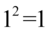 oraz wymnożenie przez
oraz wymnożenie przez 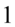 nie zmienia wyniku:
nie zmienia wyniku:
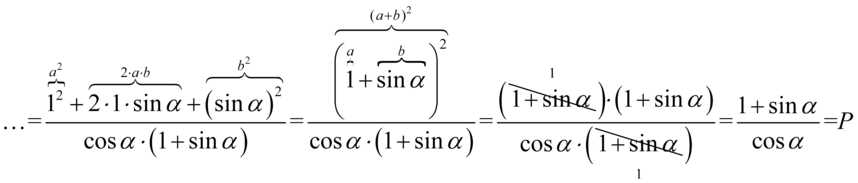
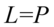
Na końcu rozpisano 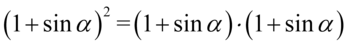 tak jak chociażby
tak jak chociażby 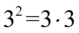 i skrócono nawias. Skracanie było możliwe, ponieważ wszelkie plusy i minusy były zamknięte w nawiasach wraz z otaczającymi je składnikami.
i skrócono nawias. Skracanie było możliwe, ponieważ wszelkie plusy i minusy były zamknięte w nawiasach wraz z otaczającymi je składnikami.