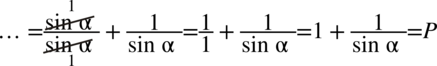Przykład 13
[kliknij aby rozwinąć] 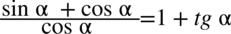
Założenie: 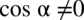 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Od razu przestrzegam przed skracaniem typu 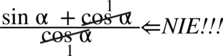 . Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami:
. Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami: 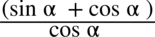 . Wnętrza nawiasu nie wolno ruszać i jak widać nie ma za bardzo z czym skrócić cosinusa z mianownika.
. Wnętrza nawiasu nie wolno ruszać i jak widać nie ma za bardzo z czym skrócić cosinusa z mianownika.
Obie strony wyrażenia są podobnej długości. Powyższy przykład można rozwiązać na dwa sposoby:
I sposób
Po prawej stronie wyrażenia jest tangens, po lewej już go nie ma. Wobec tego zaczniemy przekształcać prawą stronę do lewej zaczynając od wzoru 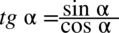 .
.
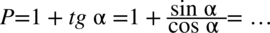
Trzeba też stworzyć kreskę ułamkową, ponieważ znajduje się ona po lewej stronie. Dokonamy tego „wrzucając” liczbę  do ułamka. Najpierw zastosujemy zapis pomocniczy
do ułamka. Najpierw zastosujemy zapis pomocniczy  , a następnie sprowadzimy składniki do wspólnego mianownika:
, a następnie sprowadzimy składniki do wspólnego mianownika:
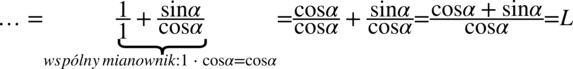

II sposób
Lewą stronę można rozdzielić na dwa ułamki tak jak się to robi na zwykłych liczbach np. 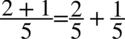 i skorzystać ze wzoru
i skorzystać ze wzoru 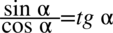
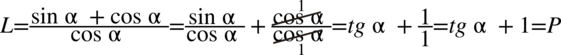

Przykład 14
[kliknij aby rozwinąć] 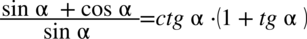
Założenie: 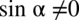 (mianownik nigdy nie może być równy
(mianownik nigdy nie może być równy  )
)
Przestrzegam przed „twórczością radosną” objawiającą się w skracaniu 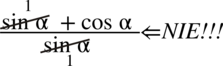 . Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami:
. Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami: 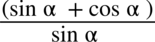 . Wnętrza
. Wnętrza
nawiasu nie wolno ruszać i jak widać nie ma za bardzo z czym skrócić sinusa z mianownika.
Obie strony wyrażenia mają podobną długość, po prawej stronie występuje tangens i cotangens, po lewej nie, poza tym po prawej stronie mamy nawias. Zaczniemy od pozbycia się nawiasów, a następnie korzystając ze wzoru 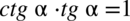 :
:
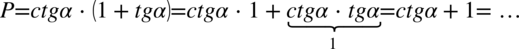
Teraz rozpiszemy cotangens zgodnie ze wzorem 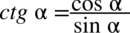 i będziemy starać się doprowadzić prawą stronę do lewej tworząc kreskę ułamkową. Dokonamy tego wrzucając
i będziemy starać się doprowadzić prawą stronę do lewej tworząc kreskę ułamkową. Dokonamy tego wrzucając  do licznika poprzez sprowadzenie do wspólnego mianownika pomocniczego wyrażenia
do licznika poprzez sprowadzenie do wspólnego mianownika pomocniczego wyrażenia  :
:
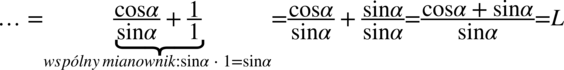

Przykład 15
[kliknij aby rozwinąć] 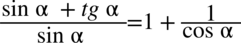
Założenie: 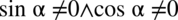 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  )
)
Przestrzegam przed „twórczością radosną” objawiającą się w skracaniu 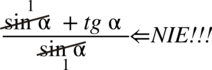 . Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami:
. Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami: 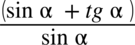 . Wnętrza
. Wnętrza
nawiasu nie wolno ruszać i jak widać nie ma za bardzo z czym skrócić sinusa z mianownika.
Lewa strona wyrażenia jest nieco dłuższa, poza tym występuje tu tangens. Można ją udowodnić na dwa sposoby krótszy i nieco dłuższy. W pierwszym (krótszym) najpierw rozbijemy ułamek tu występujący na dwa mniejsze, a później pozbędziemy się tangensa, natomiast w dłuższym wykonamy to w odwrotnej kolejności.
I sposób
Zaczniemy od rozdzielenia ułamka po lewej stronie na dwa mniejsze tak jak się to robi na prostych ułamkach 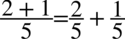 , bo po prawej nie wszystko jest na jednej kresce ułamkowej:
, bo po prawej nie wszystko jest na jednej kresce ułamkowej:
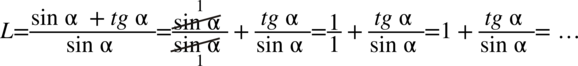
Następnie skorzystamy ze wzoru 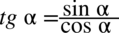 i od razu pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia. Zastosujemy później dla ułatwienia zapis
i od razu pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia. Zastosujemy później dla ułatwienia zapis 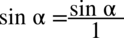 :
:
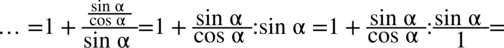


II sposób
Również zajmiemy się lewą stroną, ale zaczniemy do rozpisania tangensa ze wzoru 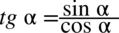 :
:

Teraz wrzucimy 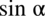 do nowo powstałego ułamka stosując zapis
do nowo powstałego ułamka stosując zapis 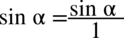 i sprowadzając oba wyrażenia z licznika mega ułamka do wspólnego mianownika:
i sprowadzając oba wyrażenia z licznika mega ułamka do wspólnego mianownika:
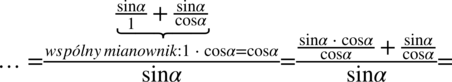
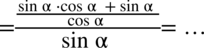
Nie powstało nic szczególnego, zatem teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia oraz zamieniając dzielenie na mnożenie dokonując odwrócenia dzielnika. Dla ułatwienia zastosujemy zapis 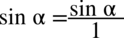 :
:
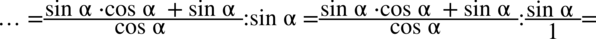

Na razie nie wolno skracać, ponieważ w liczniku pierwszego ułamka nie zamknięto dodawania w nawiasie wraz z okalającymi go elementami, ale można tu wyciągnąć 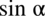 przed nawias, pamiętajmy, że w wypadku zabrania „wszystkiego” przy wyciąganiu czynnika przed nawias zostaje
przed nawias, pamiętajmy, że w wypadku zabrania „wszystkiego” przy wyciąganiu czynnika przed nawias zostaje  . Po tej operacji będzie już wolno skracać :
. Po tej operacji będzie już wolno skracać :
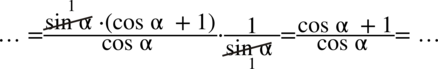
Teraz rozdzielmy powstały ułamek na dwa mniejsze tak jak się to robi na prostych ułamkach 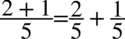 , bo po prawej nie wszystko jest na jednej kresce ułamkowej:
, bo po prawej nie wszystko jest na jednej kresce ułamkowej:
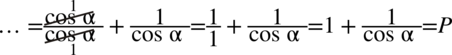

Przykład 16
[kliknij aby rozwinąć] 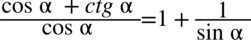
Założenie:  (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  )
)
Przestrzegam przed „twórczością radosną” objawiającą się w skracaniu typu 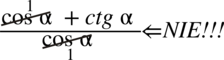 . Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami:
. Aby bezbłędnie skracać ułamek znak dodawania musi być zamknięty w nawiasie wraz z okalającymi je elementami: 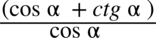 .
.
Wnętrza nawiasu nie wolno ruszać i jak widać nie ma za bardzo z czym skrócić sinusa z mianownika.
Lewa strona wyrażenia jest nieco dłuższa, poza tym występuje tu cotangens. Można ją udowodnić na dwa sposoby krótszy i nieco dłuższy. W pierwszym (krótszym) najpierw rozbijemy ułamek tu występujący na dwa mniejsze, a później pozbędziemy się cotangensa, natomiast w dłuższym wykonamy to w odwrotnej kolejności.
I sposób
Zaczniemy od rozdzielenia ułamka po lewej stronie na dwa mniejsze tak jak się to robi na prostych ułamkach 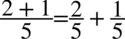 , bo po prawej nie wszystko jest na jednej kresce ułamkowej:
, bo po prawej nie wszystko jest na jednej kresce ułamkowej:
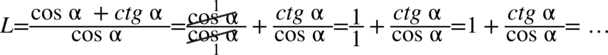
Następnie skorzystamy ze wzoru 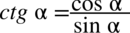 i od razu pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia. Zastosujemy później dla ułatwienia zapis
i od razu pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia. Zastosujemy później dla ułatwienia zapis 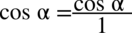 :
:
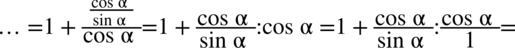
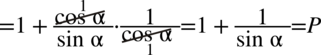

II sposób
Również zajmiemy się lewą stroną, ale zaczniemy do rozpisania cotangensa ze wzoru 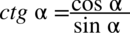 :
:
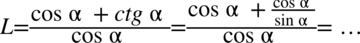
Teraz wrzucimy  do nowo powstałego ułamka stosując zapis
do nowo powstałego ułamka stosując zapis 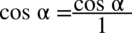 i sprowadzając oba wyrażenia z licznika mega ułamka do wspólnego mianownika:
i sprowadzając oba wyrażenia z licznika mega ułamka do wspólnego mianownika:
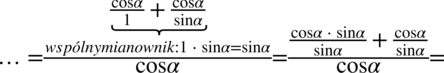
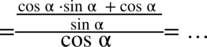
Nie powstało nic szczególnego, zatem teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia oraz zamieniając dzielenie na mnożenie dokonując odwrócenia dzielnika. Dla ułatwienia zastosujemy zapis 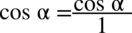 :
:
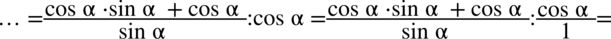
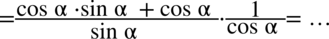
Na razie nie wolno skracać, ponieważ w liczniku pierwszego ułamka nie zamknięto dodawania w nawiasie wraz z okalającymi go elementami, ale można tu wyciągnąć  przed nawias, pamiętajmy, że w wypadku zabrania „wszystkiego” przy wyciąganiu czynnika przed nawias zostaje
przed nawias, pamiętajmy, że w wypadku zabrania „wszystkiego” przy wyciąganiu czynnika przed nawias zostaje  . Po tej operacji będzie już wolno skracać :
. Po tej operacji będzie już wolno skracać :
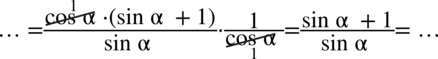
Teraz rozdzielmy powstały ułamek na dwa mniejsze tak jak się to robi na prostych ułamkach 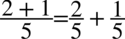 , bo po prawej nie wszystko jest na jednej kresce ułamkowej:
, bo po prawej nie wszystko jest na jednej kresce ułamkowej: