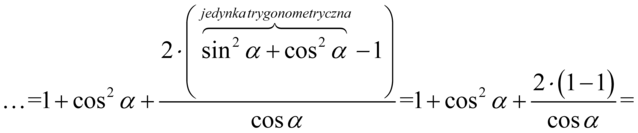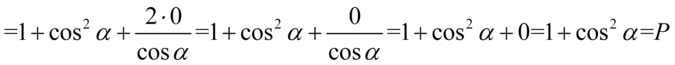Przykład 134
[kliknij aby rozwinąć] 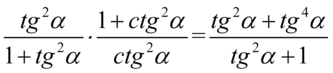
Założenie: 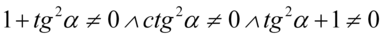 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Właściwie pierwsze i trzecie założenie jest identyczne, bo różni się jedynie kolejnością składników, także można traktować je jako jedno wyrażenie. Po przekształceniu założenia otrzymujemy
). Właściwie pierwsze i trzecie założenie jest identyczne, bo różni się jedynie kolejnością składników, także można traktować je jako jedno wyrażenie. Po przekształceniu założenia otrzymujemy 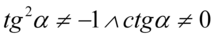 .To pierwsze jest zawsze prawdziwe, ponieważ żadna liczba rzeczywista podniesiona do kwadratu nigdy nie będzie ujemna, w drugim wyrażeniu kwadrat pominięto, ponieważ tylko zero podniesione do kwadratu daje zero, tak więc sam cotangens musi być równy zero.
.To pierwsze jest zawsze prawdziwe, ponieważ żadna liczba rzeczywista podniesiona do kwadratu nigdy nie będzie ujemna, w drugim wyrażeniu kwadrat pominięto, ponieważ tylko zero podniesione do kwadratu daje zero, tak więc sam cotangens musi być równy zero.
Przestrzegam przed skracaniem 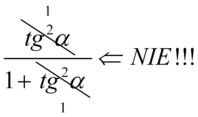 ,
, 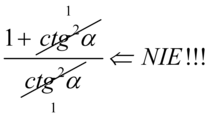 ,
, 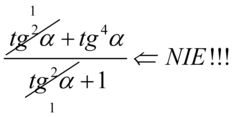 ,
, 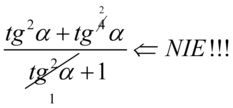 . Aby skracanie było możliwe dodawanie wraz z otaczającymi je składnikami musi być zamknięte w nawiasie:
. Aby skracanie było możliwe dodawanie wraz z otaczającymi je składnikami musi być zamknięte w nawiasie: 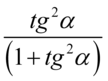 ,
, 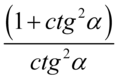 ,
, 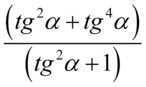 . Jak widać nie mamy możliwości skracania, ponieważ pojedynczych elementów z wnętrza nawiasu nie wolno skracać. Skraca się albo cały nawias albo nic.
. Jak widać nie mamy możliwości skracania, ponieważ pojedynczych elementów z wnętrza nawiasu nie wolno skracać. Skraca się albo cały nawias albo nic.
Lewa strona tożsamości jest dłuższa, zatem to ją będziemy przekształcać. Między kreskami ułamkowymi po lewej stronie znajduje się znak mnożenia, zatem pierwszy krok to wymnożenie obydwu ułamków (licznik przez licznik, mianownik przez mianownik):
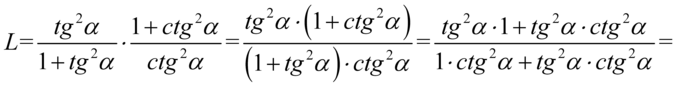
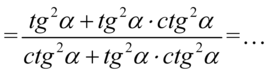
Teraz korzystając z własności potęg 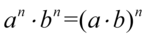 rozpiszemy
rozpiszemy 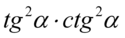 czyli:
czyli:
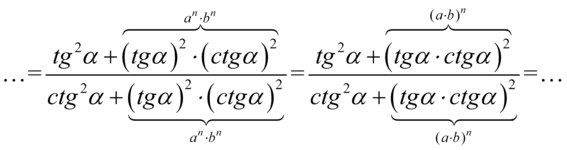
Wykonaliśmy tą operację dlatego, że 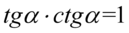 :
:
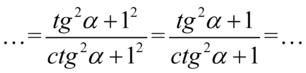
Wyrażenie znacznie się uprościło, ale w ostatecznym rozrachunku musimy uzyskać tylko tangensy, także pozbędziemy się cotangensa korzystając ze wzoru 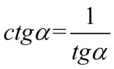 :
:
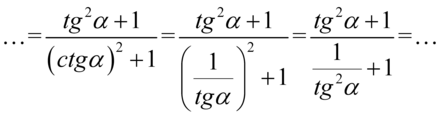
Powstał ułamek piętrowy, a więc należy dolne piętro zapisać jako pojedynczy ułamek, w tym celu sprowadzimy elementy z dołu do wspólnego mianownika. Dla ułatwienia zastosujemy zapis 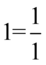 :
:
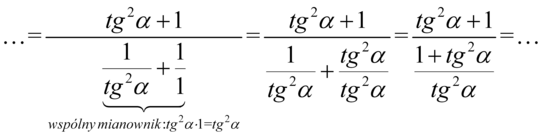
Czas na zlikwidowanie ułamka piętrowego, czyli zamiast główną kreskę ułamkową zastępujemy znakiem dzielenia i następnie zamieniamy na mnożenie odwracając drugi składnik:
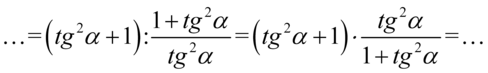
Po zamianie kreski ułamkowej na znak dzielenia należało wziąć w nawias licznik ułamka piętrowego, bo inaczej możemy się później zagubić w kolejności wykonywania działań. Powstałe wyrażenie aż się prosi o skrócenie i jest ono jak najbardziej wykonalne, ale ostateczny wynik wymaga zaniechania tej operacji, dlatego zamiast skracania wymnożymy ułamki. Dla orientacji – co z czym należy wymnożyć użyjemy zapisu 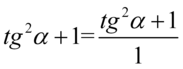 :
:
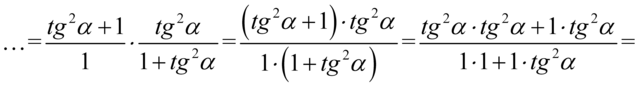
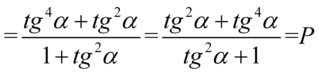
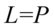
Przykład 135
[kliknij aby rozwinąć] 
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku skorzystamy dwukrotnie ze wzoru skróconego mnożenia 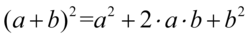 . Teraz dwie uwagi: wyniki po rozpisaniu ze wzorów najlepiej zapisywać w nawiasie, ponieważ czeka nas jeszcze kolejne działanie – w tym przypadku dodawanie. Dzięki nawiasom nie pogubimy znaków przy kolejnych działaniach. Tu akurat nic się nie stanie, ale przy odejmowaniu koniecznie zapisujmy wyniki działań w nawiasie. Druga uwaga dotyczy rozpisania ze wzoru skróconego mnożenia, ale to za chwilę:
. Teraz dwie uwagi: wyniki po rozpisaniu ze wzorów najlepiej zapisywać w nawiasie, ponieważ czeka nas jeszcze kolejne działanie – w tym przypadku dodawanie. Dzięki nawiasom nie pogubimy znaków przy kolejnych działaniach. Tu akurat nic się nie stanie, ale przy odejmowaniu koniecznie zapisujmy wyniki działań w nawiasie. Druga uwaga dotyczy rozpisania ze wzoru skróconego mnożenia, ale to za chwilę:
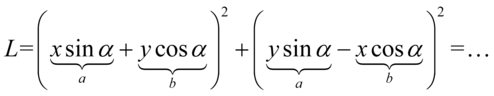
Jak widać 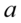 i
i 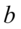 ze wzoru to „zlepek” liter i funkcji trygonometrycznych. Podnosząc składniki do potęgi koniecznie należy wziąć je w nawias! A więc
ze wzoru to „zlepek” liter i funkcji trygonometrycznych. Podnosząc składniki do potęgi koniecznie należy wziąć je w nawias! A więc 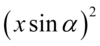 , nie
, nie 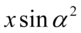 , bo kwadrat ma dotyczyć całego wyrażenia. Brak nawiasu powoduje, że kwadrat dotyczy tylko
, bo kwadrat ma dotyczyć całego wyrażenia. Brak nawiasu powoduje, że kwadrat dotyczy tylko 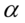 :
:

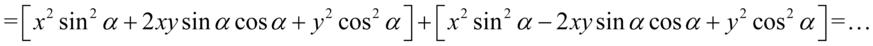
Opuszczamy nawiasy „ochronne”. Jeżeli przed nawiasem nie ma nic albo znajduje się plus, to nic się nie zmienia. Wygląda to tak jakbyśmy w ogóle zapomnieli napisać nawiasów:
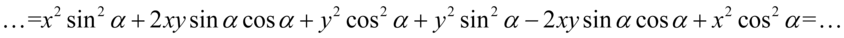
Teraz zredukujmy wyrazy podobne. Zauważmy, że  ze wzoru zredukuje się do zera:
ze wzoru zredukuje się do zera:
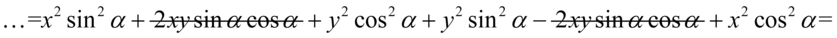
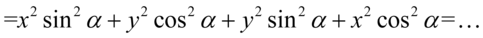
Kolejny krok to zlikwidowanie sinusów i cosinusów, w tym celu należy pogrupować w nawiasy składniki tak, aby powstała jedynka trygonometryczna po wyciągnięciu wspólnego czynnika przed nawias. Zmienimy nieco kolejność dla ułatwienia grupowania:
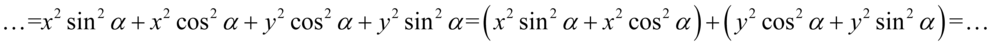
Wreszcie wyciągamy przed nawias powtarzające się elementy:
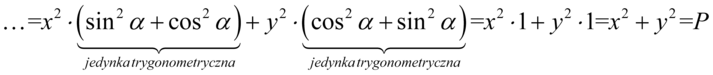
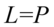
Przykład 136
[kliknij aby rozwinąć] 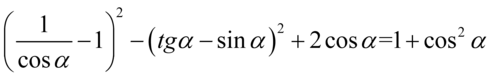
Założenie: 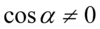 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Lewa strona równości jest zdecydowanie dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasów korzystając ze wzoru skróconego mnożenia 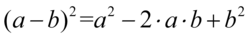 . Wyniki działań zapiszemy jeszcze w nawiasach ochronnych, ponieważ mamy do wykonania dalsze działania m. in. odejmowanie, gdzie konieczna będzie zmiana znaków, a nawiasy nie pozwolą o tym zapomnieć:
. Wyniki działań zapiszemy jeszcze w nawiasach ochronnych, ponieważ mamy do wykonania dalsze działania m. in. odejmowanie, gdzie konieczna będzie zmiana znaków, a nawiasy nie pozwolą o tym zapomnieć:
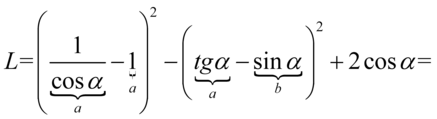
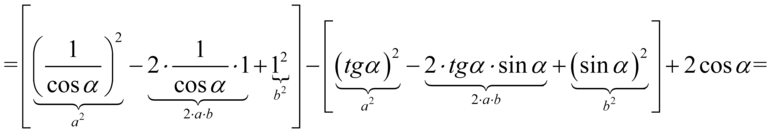
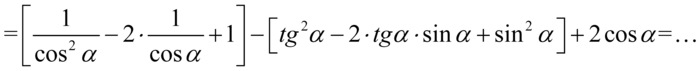
Dla ułatwienia obliczeń można zapisać 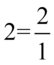 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez 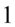 nie ulega zmianie. Tak więc jeśli ktoś ma wątpliwości jak wymnożyć
nie ulega zmianie. Tak więc jeśli ktoś ma wątpliwości jak wymnożyć 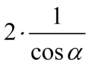 to może to zapisać
to może to zapisać 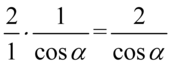 . Zlikwidujmy teraz nawiasy ochronne. Przed drugim nawiasem stoi minus, a więc opuszczając nawias zmienimy znaki na przeciwne:
. Zlikwidujmy teraz nawiasy ochronne. Przed drugim nawiasem stoi minus, a więc opuszczając nawias zmienimy znaki na przeciwne:
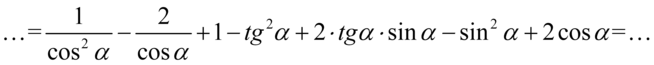
Na tym etapie nic nie można zredukować, także kolejnym krokiem jest zamiana tangensów na sinus i cosinus korzystając ze wzoru 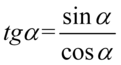 , ponieważ po prawej stronie tożsamości do której uzyskania dążymy tangensy nie występują:
, ponieważ po prawej stronie tożsamości do której uzyskania dążymy tangensy nie występują:
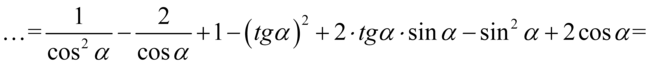
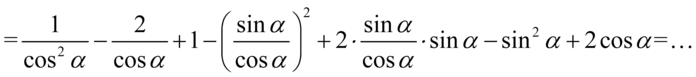
Ponownie dla ułatwienia działań użyjemy zapisu 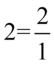 oraz
oraz 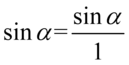 :
:
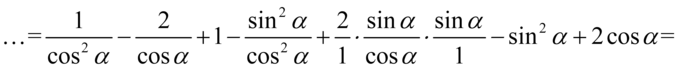
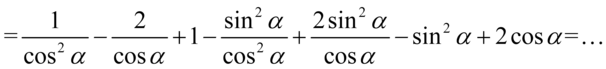
Powstały kolejne ułamki, zauważmy, że mamy dwie pary ułamków o wspólnych mianownikach. Można oczywiście próbować sprowadzać je wszystkie do wspólnego mianownika, ale łatwiej jest zawsze wykonać obliczenia, które tego nie wymagają. Zmieńmy nieco kolejność, tak aby ułamki o wspólnych mianownikach znajdowały się obok siebie i zapiszmy działania na jednej kresce:
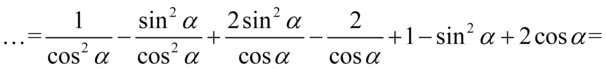
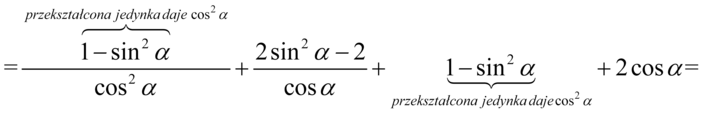
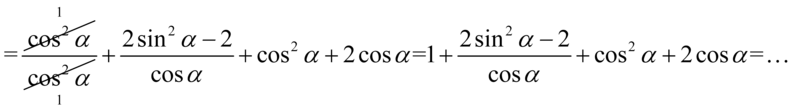
Właściwie powstały już składniki, które mamy ostatecznie otrzymać. Zapiszemy je na początku przykładu, a dla reszty ponownie znajdziemy wspólny mianownik. Dla ułatwienie działań zapiszemy 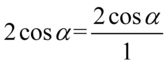 :
:
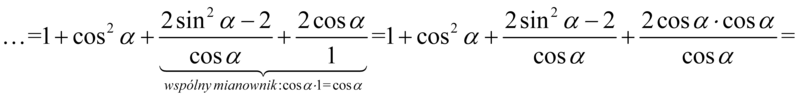
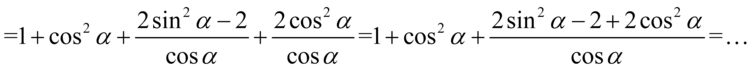
Dwójka w liczniku aż się prosi o wyciągnięcie przed nawias:
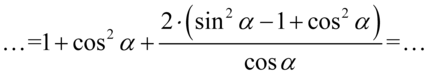
Teraz „przytulimy” 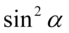 i
i 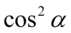 do siebie, ponieważ w ten sposób można łatwo uzyskać jedynkę trygonometryczną:
do siebie, ponieważ w ten sposób można łatwo uzyskać jedynkę trygonometryczną: