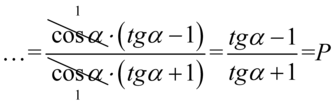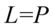Przykład 133

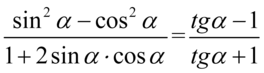
Założenie: 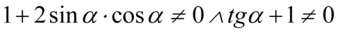(żaden mianownik nie może być równy ). Po przekształceniu założenia otrzymujemy 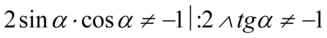i ostatecznie .

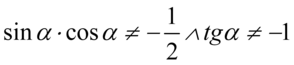Przestrzegam przed nieprawidłowym skracaniem w stylu 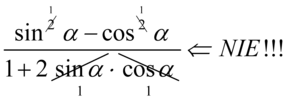lub 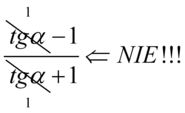. Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty w nawiasie wraz z otaczającymi elementami. Otrzymujemy wtedy 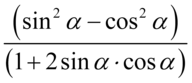oraz 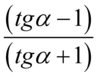. Pojedynczych elementów z nawiasu nie wolno skracać, skraca się albo całą zawartość nawiasu albo nic.

Daną tożsamość można udowodnić na dwa sposoby.

I sposób

Zajmiemy się prawą stroną. Znajdują się tam same tangensy, więc aby uzyskać lewą stronę musimy je zamienić na sinusy i cosinusy, ponieważ po tej stronie tangensy nie występują. Korzystamy ze wzoru :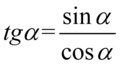

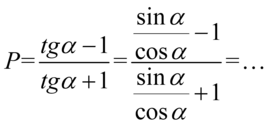
Powstał piętrowy ułamek. Najpierw każde piętro megaułamka należy zapisać jako jednolity ułamek, czyli będziemy wciągać jedynkę do zamienionego tangensa. Dla ułatwienia zastosujemy zapis :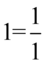

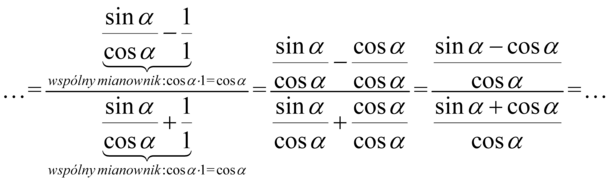
Teraz pozbędziemy się głównej kreski ułamkowej zamieniając ją na znak dzielenia, a następnie zamienimy dzielenie na mnożenie przez odwrotność drugiego ułamka:

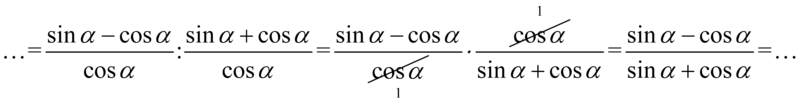
Na tym etapie należy wykonać nieco nietypowe przekształcenie – mianowicie domnożyć licznik i mianownik powstałego ułamka przez wyrażenie . Oczywiście należy użyć nawiasów aby nie pogubić znaków:

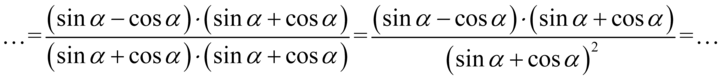
W liczniku skorzystamy ze wzoru skróconego mnożenia 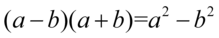, ponieważ powstały dwa nawiasy różniące się znakiem w środku, a w mianowniku użyjemy 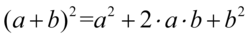. Nic się nie stanie, jeśli zaczniemy wymnażać wszystkie składniki „na piechotę”, ale użycie wzorów przyspieszy liczenie:

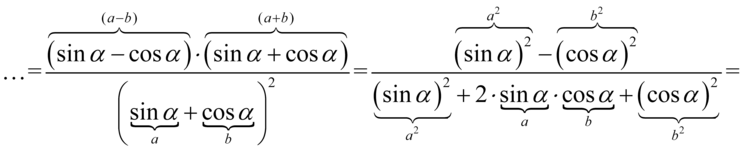
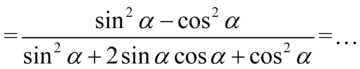
Właściwie powstał już żądany licznik, ale jeszcze należy uprościć mianownik. W tym celu „przytulimy” do siebie 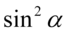oraz 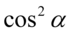. Warto wykonywać podaną czynność, ponieważ powstaje wtedy jedynka trygonometryczna:

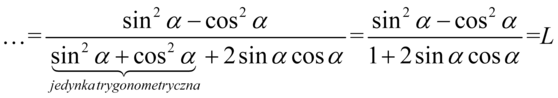
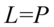
II sposób

Tym razem zajmiemy się lewą stroną tożsamości. Postąpimy tym samym dość nietypowo, ponieważ trudniej dość z sinusów i cosinusów do tangensów niż odwrotnie. Na początku rozpiszemy w mianowniku jedynkę korzystając ze wzoru na jedynkę trygonometryczną :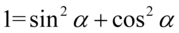

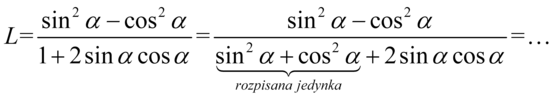
Kolejny krok to rozpoznanie wzorów skróconego mnożenia. W liczniku nie jest to aż tak trudne, ponieważ występują tu dwa składniki do parzystej potęgi oddzielone minusem. W związku z tym mamy wzór :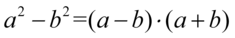

Na razie licznik zostawiamy, ponieważ nic więcej nie jesteśmy w stanie zrobić z powstałym wyrażeniem. W mianowniku również znajduje się rozpisany wzór skróconego mnożenia 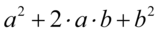. Zwiniemy go do postaci 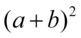. Aby łatwiej było rozpoznać ten wzór zmienię nieco kolejność elementów w mianowniku:

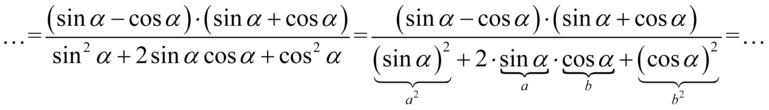
Zwijamy wzór do postaci :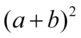

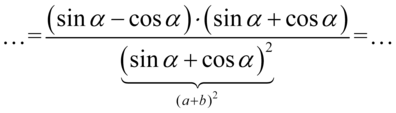
Następnie rozpiszemy mianownik na iloczyn dwóch nawiasów analogicznie jak można to wykonać na liczbach :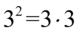

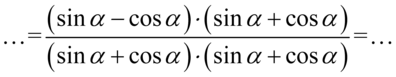
Ja widać dodawanie jest zamknięte w nawiasach, także można bez obaw skrócić cały nawias:

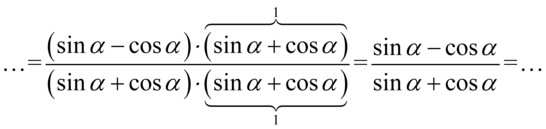
Teraz najtrudniejsza część – musimy uzyskać tangensy w liczniku i mianowniku. Wyrażenie mamy doprowadzić do postaci 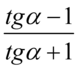. W podobnych przypadkach należy wyciągnąć sinus lub cosinus przed nawias. To liczba 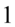wskazuje, co należy wyciągnąć przed nawias, bo jeśli zabieramy wszystko to właśnie jest to ta liczba lub wyrażenie, która stoi na miejscu jedynki. Na miejscu jedynki stoi cosinus, także to właśnie cosinus należy wyciągnąć przed nawias. Pamiętajmy, że wyciąganie czynnika przed nawias opiera się na dzieleniu wszystkich składników przez to co wyłączymy przed nawias:

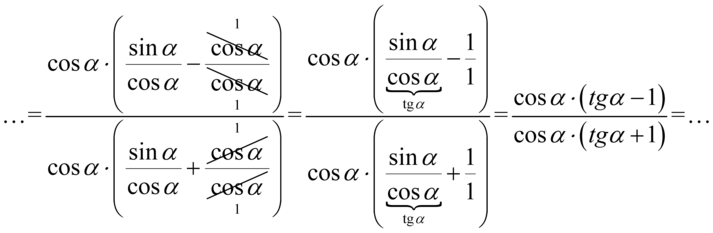
Skorzystaliśmy oczywiście ze wzoru 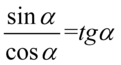. Na koniec swobodnie skrócimy cosinusy, ponieważ dodawanie jest zamknięte w nawiasie i jest to operacja dozwolona:

<./div>