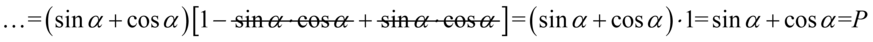Przykład 131
[kliknij aby rozwinąć] 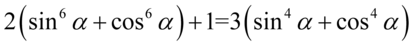
Obie strony tożsamości mają podobną długość, ale po lewej stronie mamy większe potęgi, także to ta strona będzie przekształcana. Na początku odejdziemy od schematu i nie pozbędziemy się nawiasów, tylko skorzystamy ze wzoru 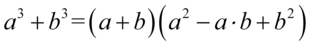 . Aby łatwiej go zauważyć wykonamy kilka wcześniejszych przekształceń korzystając z prawa działań na potęgach:
. Aby łatwiej go zauważyć wykonamy kilka wcześniejszych przekształceń korzystając z prawa działań na potęgach:

Korzystając ze wzoru 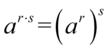 otrzymujemy:
otrzymujemy:
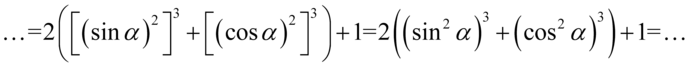
Wreszcie rozpisujemy wzór, gdzie  i
i  :
:
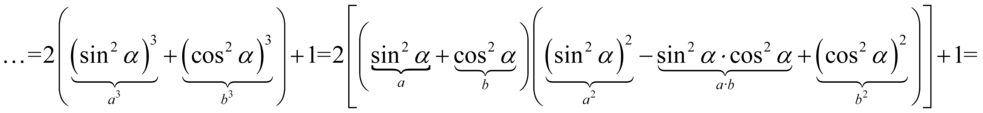
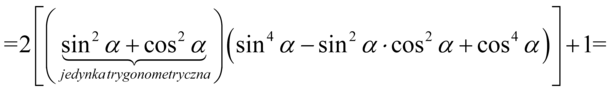
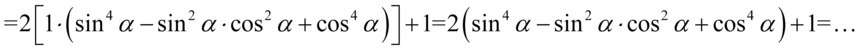
Dopiero teraz pozbędziemy się nawiasów kolejno wymnażając kolejno składniki:
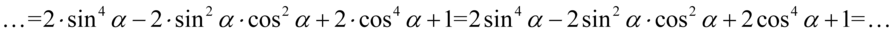
Jak widać powstały już potęgi o żądanym wykładniku, czyli 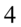 , które mamy po prawej stronie tożsamości, ale jest jeszcze kilka zbędnych wyrażeń, które również należy przekształcić. Najpierw przeniesiemy elementy z żądanymi wykładnikami na początek przykładu i nie będziemy już ich ruszać:
, które mamy po prawej stronie tożsamości, ale jest jeszcze kilka zbędnych wyrażeń, które również należy przekształcić. Najpierw przeniesiemy elementy z żądanymi wykładnikami na początek przykładu i nie będziemy już ich ruszać:
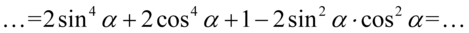
Teraz należy wykonać kilka nietypowych przekształceń. Pierwsze z nich to rozpisanie 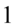 korzystając ze wzoru na jedynkę trygonometryczną (pamiętajmy na wszelki wypadek o nawiasach, żeby nie pogubić znaków – tu nic się nie stanie jeśli nie użyjemy nawiasów, bo przed jedynką stoi plus, ale warto wyrobić sobie ten nawyk):
korzystając ze wzoru na jedynkę trygonometryczną (pamiętajmy na wszelki wypadek o nawiasach, żeby nie pogubić znaków – tu nic się nie stanie jeśli nie użyjemy nawiasów, bo przed jedynką stoi plus, ale warto wyrobić sobie ten nawyk):
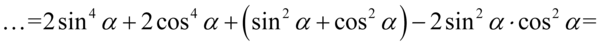
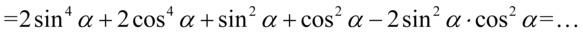
Następnie wyrażenie  rozpiszemy na dwa
rozpiszemy na dwa 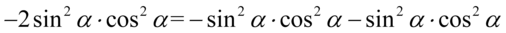 (analogicznie jak na wyrażeniach algebraicznych
(analogicznie jak na wyrażeniach algebraicznych  ) i każde z nich umieśćmy po sinusie i cosinusie z rozpisanej jedynki:
) i każde z nich umieśćmy po sinusie i cosinusie z rozpisanej jedynki:
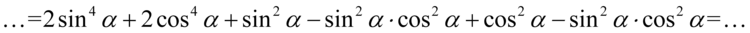
Powstałe elementy pogrupujemy po dwie sztuki w nawiasy, oczywiście pamiętamy, że nie przekształcamy już w ogóle składników z potęgą równą 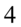 :
:
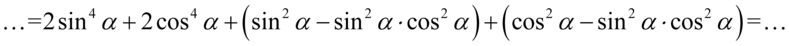
Następnie wyciągamy z każdego nawiasu możliwie największy wspólny czynnik, jeśli zabieramy wszystko, to zawsze zostaje 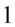 :
:

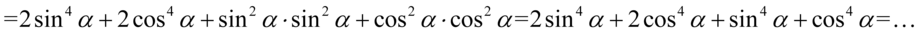
Jak widać powstały żądane wykładniki potęg i w związku z tym możemy jeszcze dokonać redukcji wyrazów podobnych, a więc w tym przypadku po prostu dodać:
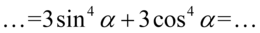
Aby uzyskać końcowy wynik wyciągamy jako wspólny czynnik trójkę przed nawias:
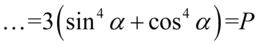
Przykład 132
[kliknij aby rozwinąć] 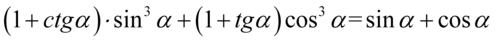
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Zaczniemy od likwidacji nawiasów kolejno wymnażając składniki:
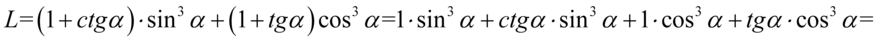
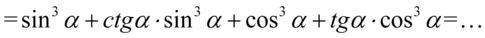
Kolejny krok to zamiana cotangensa i tangensa na sinus i cosinus, ponieważ po prawej stronie tożsamości, do której uzyskania dążymy znajduje się tylko sinus i cosinus. Oczywiście korzystamy ze wzorów 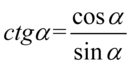 oraz
oraz 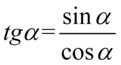 :
:
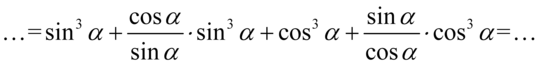
Teraz nieco uprościmy powstałe wyrażenie tzn. wymnożymy ułamki, aby ułatwić zrozumienie skracania zapiszemy 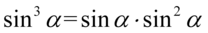 - analogicznie można postąpić z cosinusem. Jeszcze tylko dla ułatwienia zastosujemy zapis
- analogicznie można postąpić z cosinusem. Jeszcze tylko dla ułatwienia zastosujemy zapis 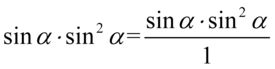 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez 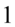 nie ulega zmianie):
nie ulega zmianie):
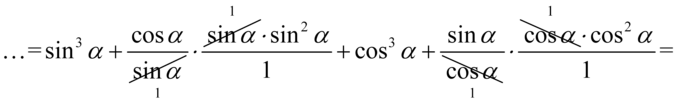
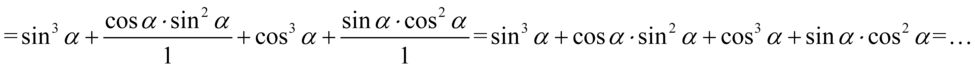
Od tego momentu można dokonać przekształceń idąc w dwóch kierunkach.
I sposób
Będziemy grupować składniki wyrażenia w dwa nawiasy po dwa elementy co oczywiście nie zmieni wartości całego wyrażenia:
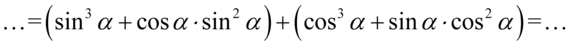
Teraz z każdego nawiasu wyciągniemy możliwie największy wspólny czynnik czyli powtarzający się element:

Jak widać powstały dwa identyczne nawiasy, które w tym momencie stają się wspólnym czynnikiem. Inaczej mówiąc należy przepisać raz powtarzający się nawias, a w drugim nawiasie zapiszemy „sieroty”, które zostały po zabraniu tegoż nawiasu. Wygląda to tak:
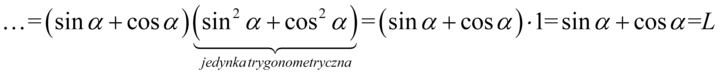
II sposób
Sposób ten również opiera się na grupowaniu w nawiasy, ale zanim zostanie to wykonane zmienimy nieco kolejność składników:
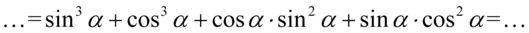
I grupujemy w dwa nawiasy po dwie sztuki:
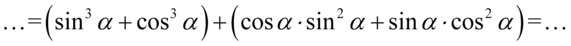
W pierwszym nawiasie powstał wzór skróconego mnożenia postaci 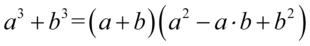 i będziemy go rozpisywać, a z drugiego nawiasu wyciągniemy największy wspólny czynnik
i będziemy go rozpisywać, a z drugiego nawiasu wyciągniemy największy wspólny czynnik 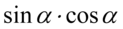 . Dla większej przejrzystości pierwszy okrągły nawias zastąpiono kwadratowym:
. Dla większej przejrzystości pierwszy okrągły nawias zastąpiono kwadratowym:

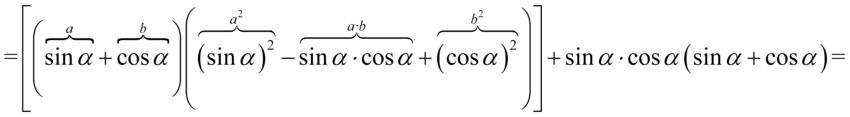
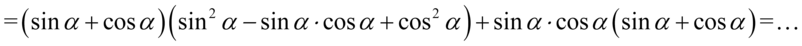
Teraz zmienimy nieco kolejność składników tzn. warto „przytulać” do siebie sinusy i cosinusy podniesione do kwadratu, ponieważ dzięki temu uzyskujemy jedynkę trygonometryczną:
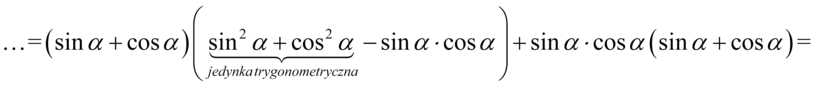
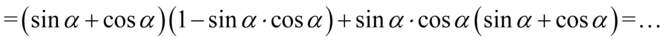
Ponownie powstały dwa powtarzające się nawiasy, także znów przepisujemy powtarzający się nawias jako wspólny czynnik, a „sieroty” umieszczamy w drugim nawiasie. Aby wizualnie było przejrzyście ten drugi nawias będzie kwadratowy, ponieważ jedna z „sierot” jest nawiasem:
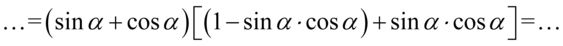
Opuśćmy nawiasy wewnętrzne i zredukujmy wyrazy podobne: